To tylko jedna z 15 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
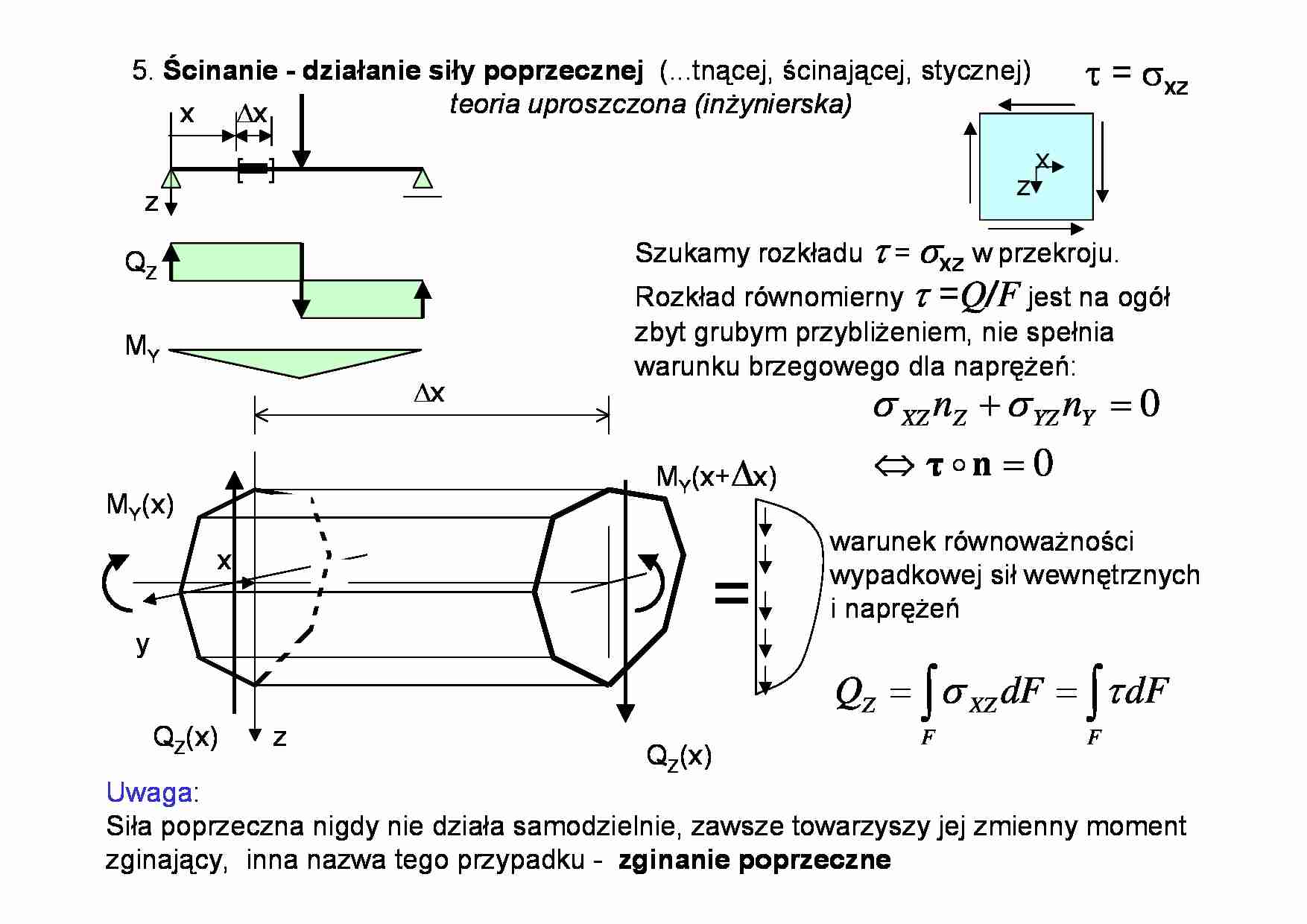
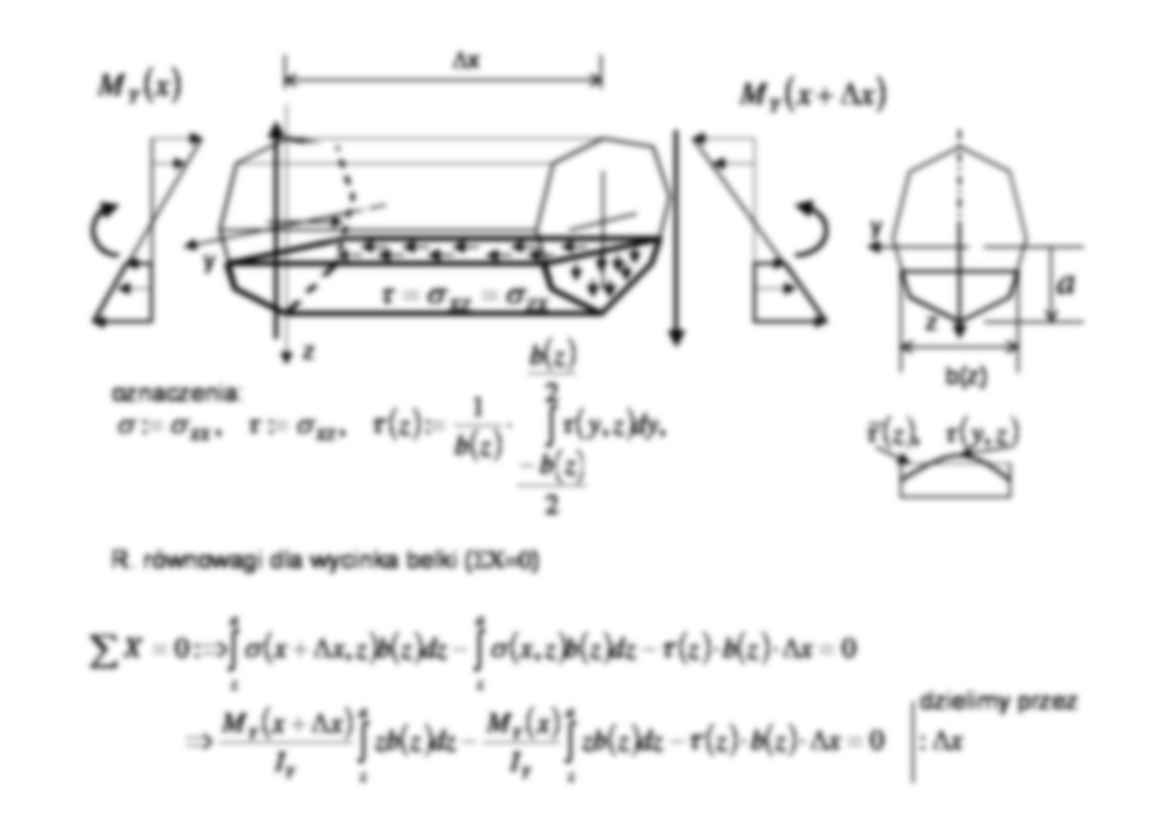
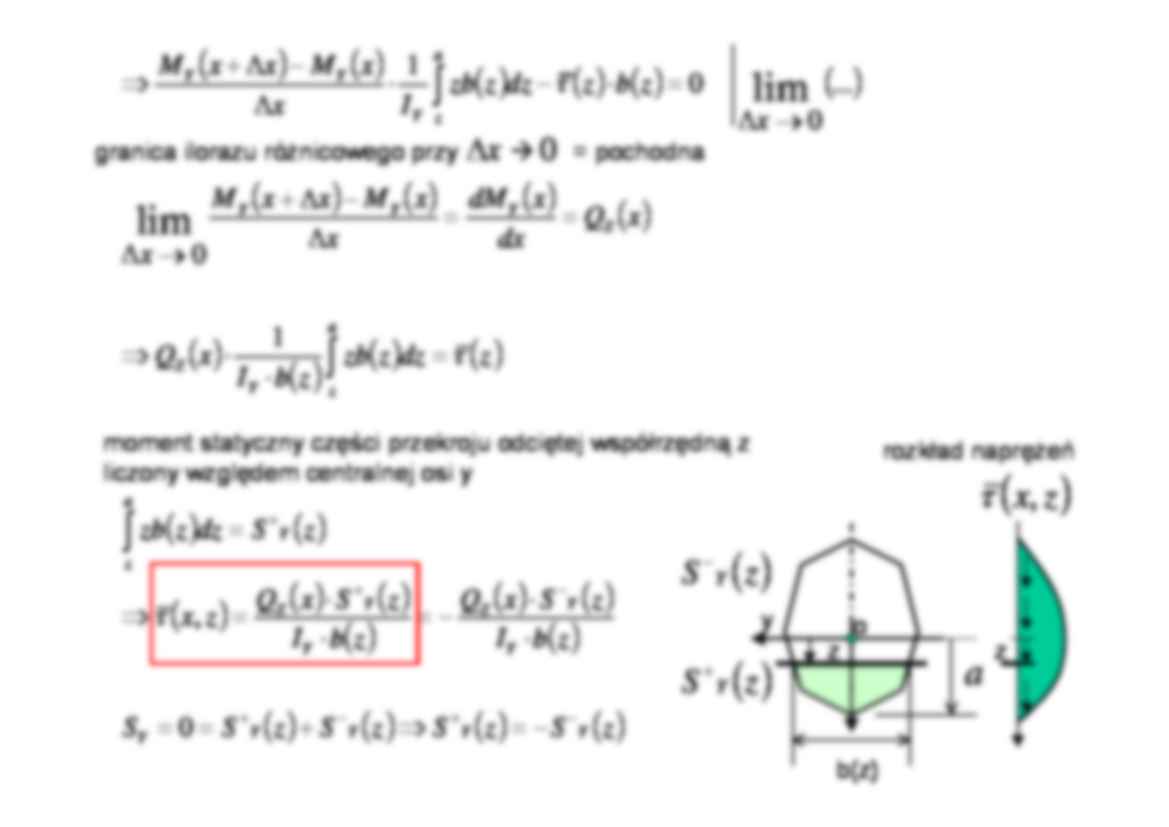
5. Ścinanie - działanie siły poprzecznej (...tnącej, ścinającej, stycznej) teoria uproszczona (inżynierska) x z τ = σ xz Szukamy rozkładu τ = σ xz w przekroju. Rozkład równomierny τ = Q / F jest na ogół zbyt grubym przybliżeniem, nie spełnia warunku brzegowego dla naprężeń: 0 0 = ⇔ = + n τ o Y YZ Z XZ n n σ σ dF dF Q F F XZ Z ∫ ∫ = = τ σ warunek równoważności wypadkowej sił wewnętrznych i naprężeń Δx z y x Q Z(x) = M Y(x) Q Z(x) M Y(x+Δx) Uwaga: Siła poprzeczna nigdy nie działa samodzielnie, zawsze towarzyszy jej zmienny moment zginający, inna nazwa tego przypadku - zginanie poprzeczne [ ] Q Z x Δx z M Y y z Δx ( ) x M Y ( ) x x M Y Δ + R. równowagi dla wycinka belki ( ΣX=0) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) x x z b z dz z zb I x M dz z zb I x x M x z b z dz z b z x dz z b z x x X dy z b z b z y z b z a z Y Y a z Y Y a z a z XZ XX Δ = Δ ⋅ ⋅ − − Δ + ⇒ = Δ ⋅ ⋅ − − Δ + ⇒ = − ⋅ = = = ∫ ∫ ∫ ∫ ∑ ∫ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ : 0 0 , , : 0 , 2 2 , 1 : , : , : τ τ σ σ τ τ σ τ σ σ ( ) ( ) z y z , , τ τ b(z) y a z dzielimy przez oznaczenia: ZX XZ σ σ τ = = ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) z S z S z S z S S z b I z S x Q z b I z S x Q z x z S dz z zb z dz z zb z b I x Q x Q dx x dM x x M x x M x x z b z dz z zb I x x M x x M Y Y Y Y Y Y Y Z Y Y Z Y a z a z Y Z Z Y Y Y a z Y Y Y − + − + − + + − = ⇒ + = = ⋅ ⋅ − = ⋅ ⋅ = ⇒ = = ⋅ ⋅ ⇒ = = Δ − Δ + → Δ → Δ = ⋅ − ⋅ Δ − Δ + ⇒ ∫ ∫ ∫ 0 , 1 0 ... 0 0 1 lim lim τ τ τ granica ilorazu różnicowego przy Δ x 0 = pochodna moment statyczny części przekroju odciętej współrzędną z liczony względem centralnej osi y rozkład naprężeń b(z) y a z ( ) z S Y + ( ) z S Y − ( ) z x , τ z o Przykład 1. Prostokąt b h y ( ) z ( ) ( ) ( ) ⎟ ⎟
(…)
… postaciowego
GF I Y F
GF
SY ( z )
+ 2
F
k= 2
I Y ∫ b 2 (z ) dF
F
energetyczny współczynnik ścinania
Mechanika budowli: we wzorze Maxwella-Mohra
(zasada prac wirtualnych dla układów prętowych):
l l l
1 ⋅ Δ p = ∑ ( ∫ κ i M p dx + ∫ ε i N p dx + ∫ β i Q p dx) =
0 0 0
l l l
wpływ ścinania
MiM p Ni N p Qi Q p
= ∑ (∫ dx + ∫ dx + ∫ k dx)
0
EI 0
EF 0
GF
1 h h
1.prostokąt F S (z ) F S (z )
+2 2 +2 bh 2
k= 2 ∫ dF = 2…
…
+ ⎟ =
5 ⎟ −1
⎠
144 ⎛ 2 2 ⎞ 144 ⎛ 30 10 6 ⎞ 144 16 6
⎜2 − 2 + ⎟ = ⎜ −2 + ⎟ = ⋅ = =k
128 ⎝ 3 5 ⎠ 128 ⎝ 15 15 15 ⎠ 128 15 5
2.koło, 3. dwuteownik
32
k= k=
F
(≅ 2.4 ÷ 2.0 dla I walcowanych)
27 FSR
wpływ ścinania na ugięcie belek
L/2 L/2 L/2
P
L
M1 ⋅ M ⎛ ⎞ PL / 4 1 L PL L 1 1 PL3
x Δ =M ∫
0
EI
dx = 2⎜ ⎜
⎝
⎟
⎟ L / 4 ⋅ EI = 2 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 4 ⋅ EI = 48 EI
⎠
z
M ⋅M Q ⋅Q
L L
Δ MQ = Δ M + ΔQ = ∫ 1 dx + ∫ k 1 dx =
Q…
… postaciowego
∫ b 2 (z )
GF
F
2
F
k= 2
I Y
+
SY ( z )
∫ b 2 (z ) dF
F
2
energetyczny współczynnik ścinania
Mechanika budowli: we wzorze Maxwella-Mohra
(zasada prac wirtualnych dla układów prętowych):
l
l
l
0
0
0
1 ⋅ Δ p = ∑ ( ∫ κ i M p dx + ∫ ε i N p dx + ∫ β i Q p dx) =
l
= ∑ (∫
0
MiM p
EI
l
dx + ∫
0
Ni N p
EF
l
dx + ∫ k
0
Qi Q p
GF
wpływ ścinania
dx)
1.prostokąt
h
y
z
b
1
F S (z )
F S (z )
b
/
bdz =
dF = 2…
... zobacz całą notatkę






Komentarze użytkowników (0)