To tylko jedna z 13 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
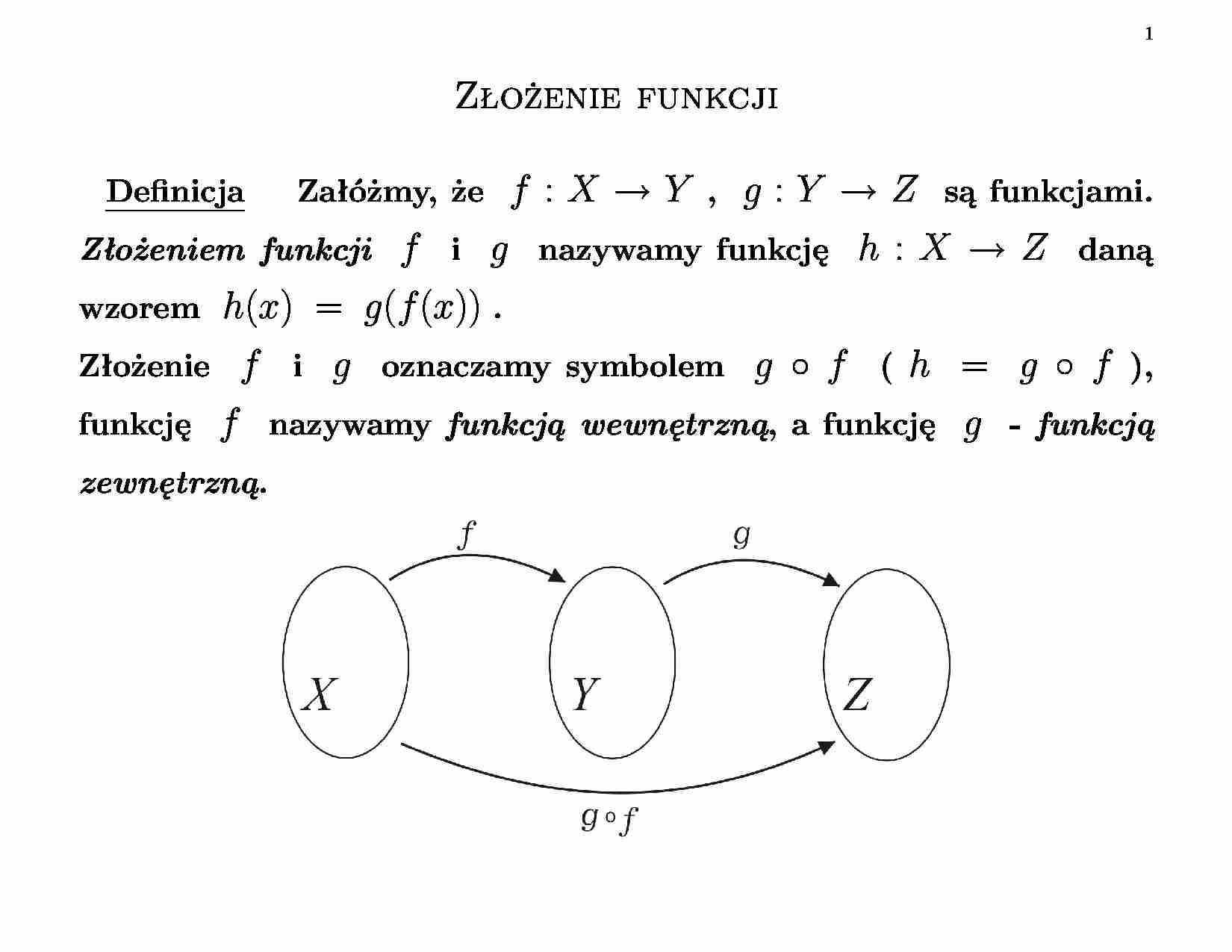


1 Złożenie funkcji Definicja Załóżmy, że f : X → Y , g : Y → Z są funkcjami. Złożeniem funkcji f i g nazywamy funkcję h : X → Z daną wzorem h ( x ) = g ( f ( x )) . Złożenie f i g oznaczamy symbolem g ◦ f ( h = g ◦ f ), funkcję f nazywamy funkcją wewnętrzną , a funkcję g - funkcją zewnętrzną . 2 Uwaga • Złożenie dwóch funkcji rosnących jest funkcją rosnącą. • Złożenie dwóch funkcji malejących jest funkcją rosnącą. • Złożenie funkcji rosnącej i funkcji malejącej jest funkcją malejącą. Przykład Określmy funkcje złożone f ◦ f , f ◦ g , g ◦ f , g ◦ g , jeżeli f ( x ) = x 2 i g ( x ) = √ x . 3 Funkcja odwrotna Definicja Funkcję f : X → Y nazywamy funkcją różnowartościo- wą (injekcją) , jeżeli ∀x 1 ,x 2 ∈X ( x 1 = x 2 ) = ⇒ f ( x 1) = f ( x 2) . Funkcję różnowartościową będziemy oznaczać: f : X 1 − 1 −→ Y . Definicja Funkcję f : X → Y nazywamy funkcją ”na” (surjekcją) , jeżeli Wf = Y , tzn. ∀y∈Y ∃x∈X y = f ( x ) . Funkcję ”na” będziemy oznaczać: f : X na −→ Y . 4 Definicja Funkcję, która jest jednocześnie ”1-1” i ”na” nazywamy funkcją wzajemnie jednoznaczną (bijekcją) i oznaczamy f : X 1 − 1 −→ na Y . Przykład Czy funkcje zilustrowane grafami lub wykresami są różnowartościowe i ”na” ? 5 6 Uwaga • Złożenie dwóch funkcji różnowartościowych jest funkcją różnowarto- ściową. • Funkcja ściśle monotoniczna jest funkcją różnowartościową. Przykład Sprawdźmy, czy funkcja a ) f ( x ) = 2 x − 3 x + 1 b ) f ( x ) = 3 x + 2 x − 4 jest różnowartościowa w swojej dziedzinie. 7 Definicja Niech f : X → Y będzie funkcja wzajemnie jednoznaczną. Funkcję f − 1 : Y → X nazywamy funkcją odwrotną do funkcji f , jeżeli dla każdego x ∈ X i y ∈ Y f − 1( y ) = x ⇐⇒ y = f ( x ) . f − 1 ◦ f = IdX ( f − 1 ◦ f )( x ) = f − 1( f ( x )) = f − 1( y ) = x f ◦ f − 1 = IdY ( f ◦ f − 1)( y ) = f ( f − 1( y )) = f ( x ) = y 8 Uwaga Wykres funkcji odwrotnej otrzymujemy z wykresu funkcji danej, odbijając go symetrycznie względem prostej y = x . Przykład Wyznaczmy funkcję odwrotną do funkcji: • y = 1 2 x + 1 x ∈ R • y = x 2 − x x ∈ [1 , + ∞ )
(…)
…
(f −1 ◦ f )(x) = f −1(f (x)) = f −1(y) = x
f ◦ f −1 = IdY
(f ◦ f −1)(y) = f (f −1(y)) = f (x) = y
8
Uwaga Wykres funkcji odwrotnej otrzymujemy z wykresu funkcji
danej, odbijając go symetrycznie względem prostej y = x .
Przykład
Wyznaczmy funkcję odwrotną do funkcji:
• y = 1x + 1
2
• y = x2 − x
x∈R
x ∈ [1, +∞)
9
Funkcje wymierne
Definicja
Funkcją wymierną nazywamy funkcję postaci:
W(x)
y =
,
Q(x)
gdzie W(x) i Q(x) są wielomianami, przy czym Q(x) nie jest
wielomianem zerowym.
Dziedziną funkcji wymiernej jest zbiór tych liczb rzeczywistych, dla
których Q(x) = 0.
W szczególności:
10
a
Funkcję y = , a = 0 nazywamy proporcjonalnością odwrotną.
x
a
jest
Jej dziedziną jest zbiór R
{0} . Wykresem funkcji y =
x
hiperbola.
11
ax + b
Funkcję y =
cx + d
ad − bc = 0 i c = 0.
nazywamy funkcją homograficzną…
... zobacz całą notatkę






Komentarze użytkowników (0)