To tylko jedna z 11 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
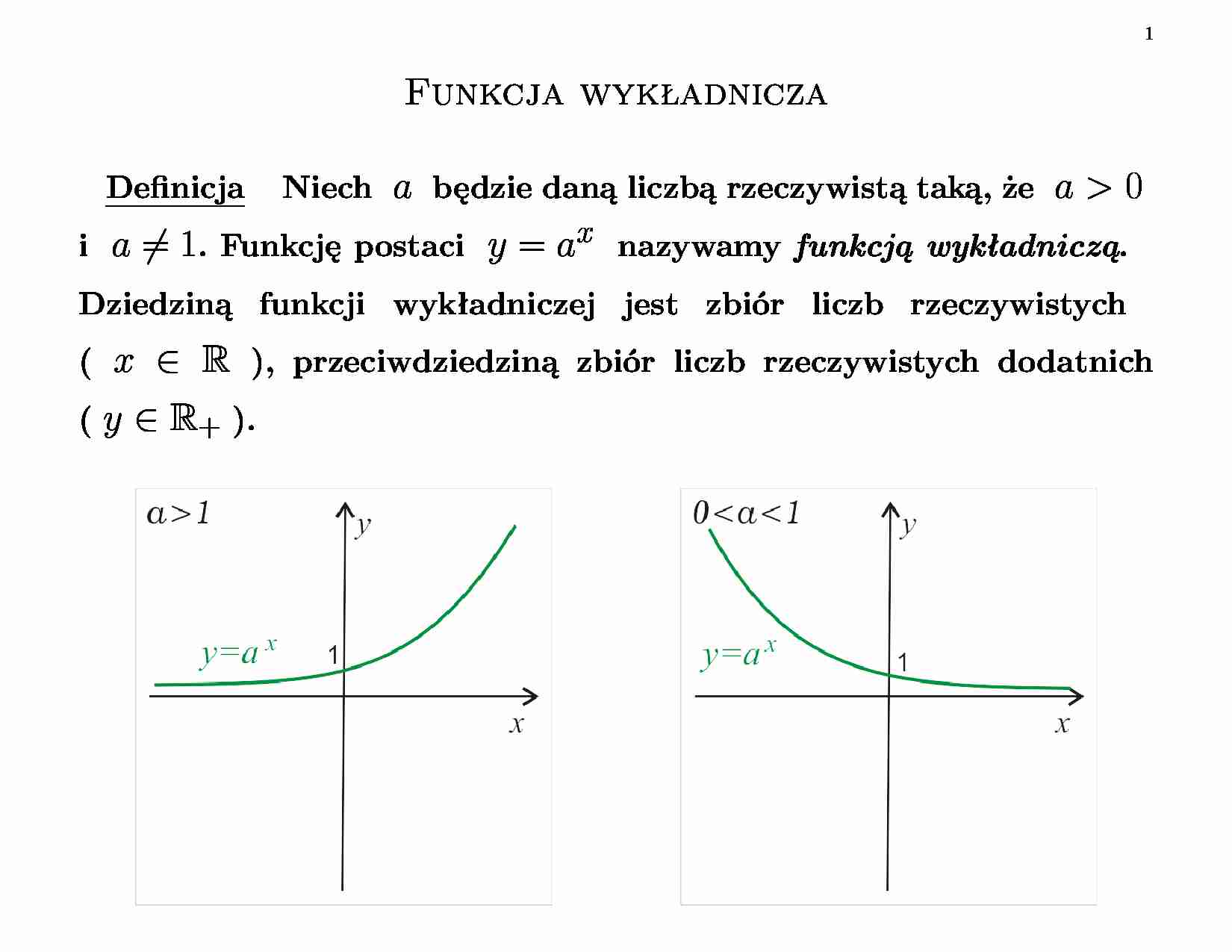


1 Funkcja wykładnicza Definicja Niech a będzie daną liczbą rzeczywistą taką, że a 0 i a = 1 . Funkcję postaci y = ax nazywamy funkcją wykładniczą . Dziedziną funkcji wykładniczej jest zbiór liczb rzeczywistych ( x ∈ R ), przeciwdziedziną zbiór liczb rzeczywistych dodatnich ( y ∈ R+ ). 2 Spośród nieskończenie wielu funkcji wykładniczych najważniejszą rolę odgrywają dwie: y = 10 x i y = ex , gdzie liczba e = 2 , 7182818284590452353602874713526624977572470936999 . . . jest niewymierna ( e ≈ 2 , 72 ). Liczba e nosi nazwę liczby Eulera (Nepera). Własności funkcji wykladniczej • Funkcja wykładnicza jest funkcją różnowartościową. Oznacza to, że dla a 0 i a = 1 a x 1 = ax 2 ⇐⇒ x 1 = x 2 . • Dla a 1 funkcja wykładnicza y = ax jest funkcją rosnącą, bo 3 dla dowolnych x 1 , x 2 ∈ R x 1 ax 2 . Przykład Dla jakich wartości zmiennej x funkcje f i g mają równe wartości: a) f ( x ) = 2 5 4 − 4 x , g ( x ) = 1 2 3 x 2 b) f ( x ) = 0 , 75 x− 1 3 , g ( x ) = 4 3 6 x 2 4 Przykład Dla jakich wartości zmiennej x funkcja f ( x ) = 5 2 x +1 − 5 x przyjmuje wartości dodatnie? Przykład Dane są funkcje f ( x ) = 4 x +1 − 7 · 3 x i g ( x ) = 3 x +2 − 5 · 4 x . Rozwiązać nierówność f ( x ) g ( x ) . 5 Logarytm Definicja Logarytmem liczby rzeczywistej x 0 przy podstawie a ( a 0 i a = 1 ) nazywamy wykładnik potęgi y , do której należy podnieść liczbę a , żeby otrzymać x , tj. log a x = y ⇐⇒ a y = x. Na przykład: log2 8 = 3 , bo 2 3 = 8 . Logarytm log10 x nazywamy logarytmem dziesiętnym i oznaczamy krótko log x . Logarytm log e x nazywamy logarytmem naturalnym i oznaczamy krótko ln x . 6 Własności logarytmu • log a 1 = 0 • log a a = 1 • log a a y = y • a log a x = x , gdzie a 0 i a = 1 oraz x 0 i y ∈ R . Twierdzenie (Własności działań na logarytmach) Dla dowolnych liczb rzeczywistych dodatnich x , y , a , b ( a = 1 , b = 1 ) i p ∈ R zachodzą wzory: • log a ( x · y ) = log a x + log a y •
(…)
…, bo dla dowolnych x1, x2
0 < x1 < x2
=⇒
loga x1 < loga x2.
• Dla 0 < a < 1 funkcja logarytmiczna y = loga x jest funkcją
malejącą, bo dla dowolnych x1, x2
0 < x1 < x2
=⇒
loga x1 > loga x2.
10
y = loga x jest funkcją odwrotną do
funkcji wykładniczej y = ax.
• Funkcja logarytmiczna
Przykład
Wyznaczyć dziedzinę funkcji:
a) f (x) = log7 log0,5(x2 − 7x + 12) + 1
b) f (x) = log3 log0,5(x + 2) + 2
Wykazać, że wykresy…
… y
y
• loga xp = p · loga x
logb x
1
• loga x =
, w szczególności loga b =
.
logb a
logb a
7
Przykład
Obliczyć:
a) log√2 0, 25
b)
1 −log
1000 3
Przykład
log14 5 = b.
c) log 1 3
√
3
√
3
3
9
3
d) 92 log3 2+4 log81 2
Obliczyć log35 28 , jeżeli wiadomo, że log14 2 = a i
8
Funkcja logarytmiczna
Definicja
Niech
a
będzie daną liczbą rzeczywistą taką, że
a > 0 i a = 1. Funkcję postaci y = loga x nazywamy…
... zobacz całą notatkę






Komentarze użytkowników (0)