7-stronicowa notatka z algebry liniowej w formacie doc. Zadania z macierzami oraz podstawowe definicje związane z tematem, twierdzenia, przykłady. Zagadnienia omówione w notatce to między innymi: bazowa postać macierzy, rozwiązywanie równań macierzowych, rachunek macierzowy, macierz odwrotna, przestrzeń liniowa, ciało, struktura, wektor przeciwny, definicja przestrzeni liniowej, przykłady przestrzeni liniowych, wektor zerowy, definicja równoległości wektorów, definicja podprzestrzeni liniowej E, elementarna definicja iloczynu skalarnego, własności iloczynu skalarnego, kowektor, definicja formalna iloczynu skalarnego, przestrzeń unitarna, nierówność Schwartza.
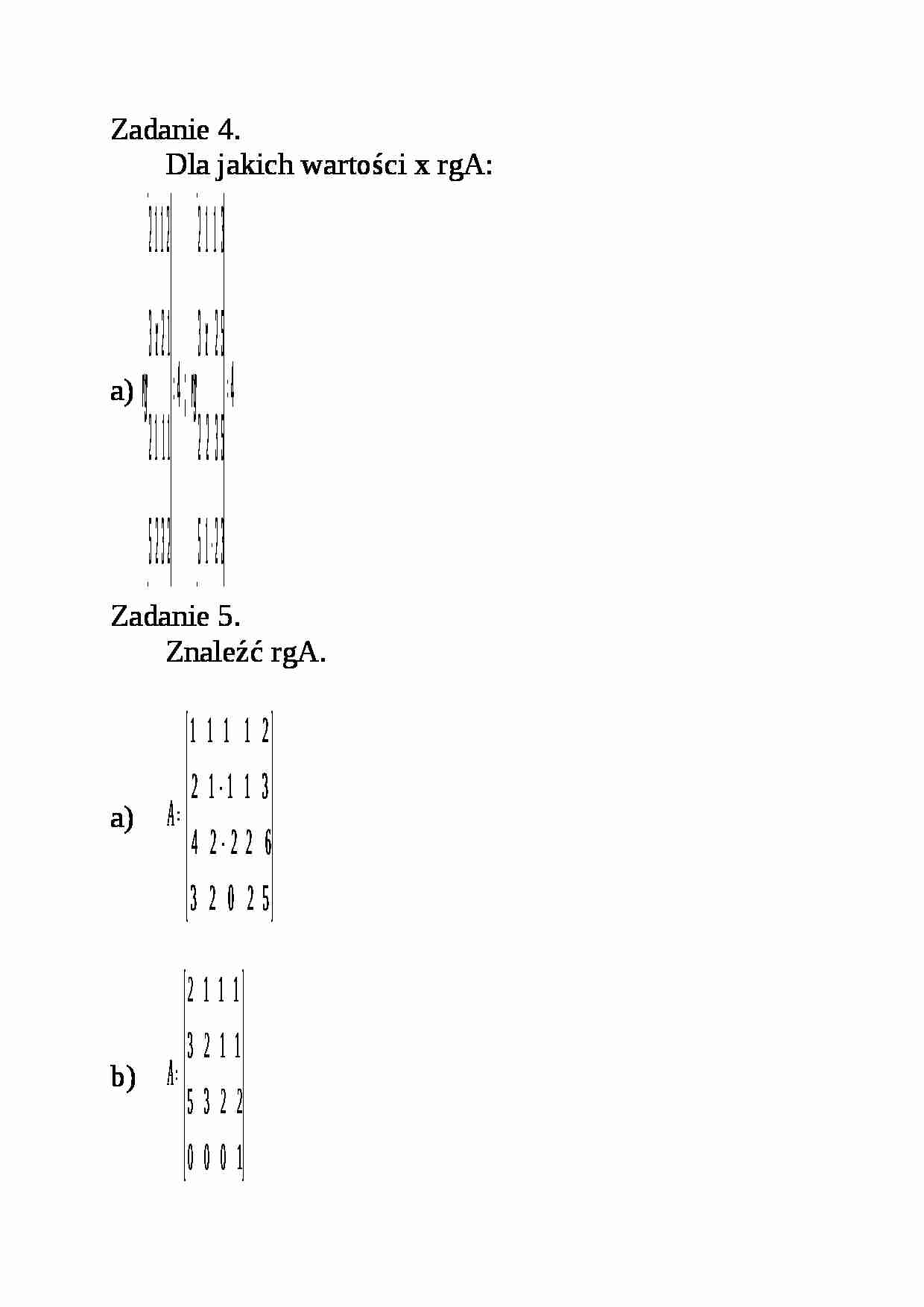
Zadanie 4.
Dla jakich wartości x rgA:
a) Zadanie 5.
Znaleźć rgA.
a) b) c) Zad. 6. Sprowadzić macierz do postaci bazowej: lub podobnej.
a) b) c) Zad.7.
Rozwiązać r-nie macierzowe (metodą A-1)
a) b) P5.
Wyznaczyć rgA poprzez znalezienie postaci bazowej A
rgA = rgI2 = 2
PRZESTRZEŃ LINIOWA
W E ≠ ∅ jest określona struktura przestrzeni liniowej nad ciałem R, jeżeli w E określone jest działanie:
Ponadto jest określone mnożenie el-tów zbioru E poprzez liczby:
Definicja przestrzeni liniowej.
Wówczas E nazywamy przestrzenią liniową (wektorową). Wektor 0∈E oznaczamy 0.
Przykłady przestrzeni liniowych:
Przestrzeń macierzy [aij]n x m z działaniami dodawania macierzy i mnożenia macierzy przez liczbę
Zbiór wszystkich funkcji o wartościach rzeczywistych określonych na dowolnym zbiorze X ≠ ∅ z działaniami Twierdzenie 1.
Własności przestrzeni liniowej:
istnieje tylko jeden wektor 0
istnieje dokładnie jeden wektor (-x)
Definicja równoległości wektorów:
Wektory x, y ≠ 0 są równoległe, jeżeli istnieje taka liczba α∈R, że x = α⋅y
Definicja podprzestrzeni liniowej E:
Zbiór V nazywamy podprzestrzenią przestrzeni liniowej E, jeżeli:
1) 2) Wniosek 1.
Każda podprzestrzeń przestrzeni E jest też przestrzenią linową.
Przykład 6.
Niech E = R1xn - macierze o el-tach ∈R postaci [a1,...,an] (wektory w Rn).
Niech V = {x∈E : x = (x1,...,xk; 0,...,0)}, wówczas V jest podprzestrzenią E.
Przykład 7.
Zbiór V macierzy a, b∈R jest podprzestrzenią liniową przestrzeni złożonej z a,b,c,d∈R
Definicja iloczynu skalarnego (elementarna)
Niech x, y ∈Rn,1(lub R1,n)
(lub xyT) kowektor
Własności iloczynu skalarnego
- W1
- W2 - W3 Definicja formalna iloczynu skalarnego
W przestrzeni liniowej E jest określony iloczyn skalarny, gdy każdej parze wektorów x, y∈E jest przyporządkowana liczba (xy) spełniająca warunki W1 i W2 i W3.
Definicja przestrzeni euklidesowej (skończonego wymiaru):
Przestrzeń liniową, w której określono iloczyn skalarny nazywamy przestrzenią euklidesową (unitarną).
Nierówność Schwartza:
... zobacz całą notatkę





Komentarze użytkowników (0)