To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
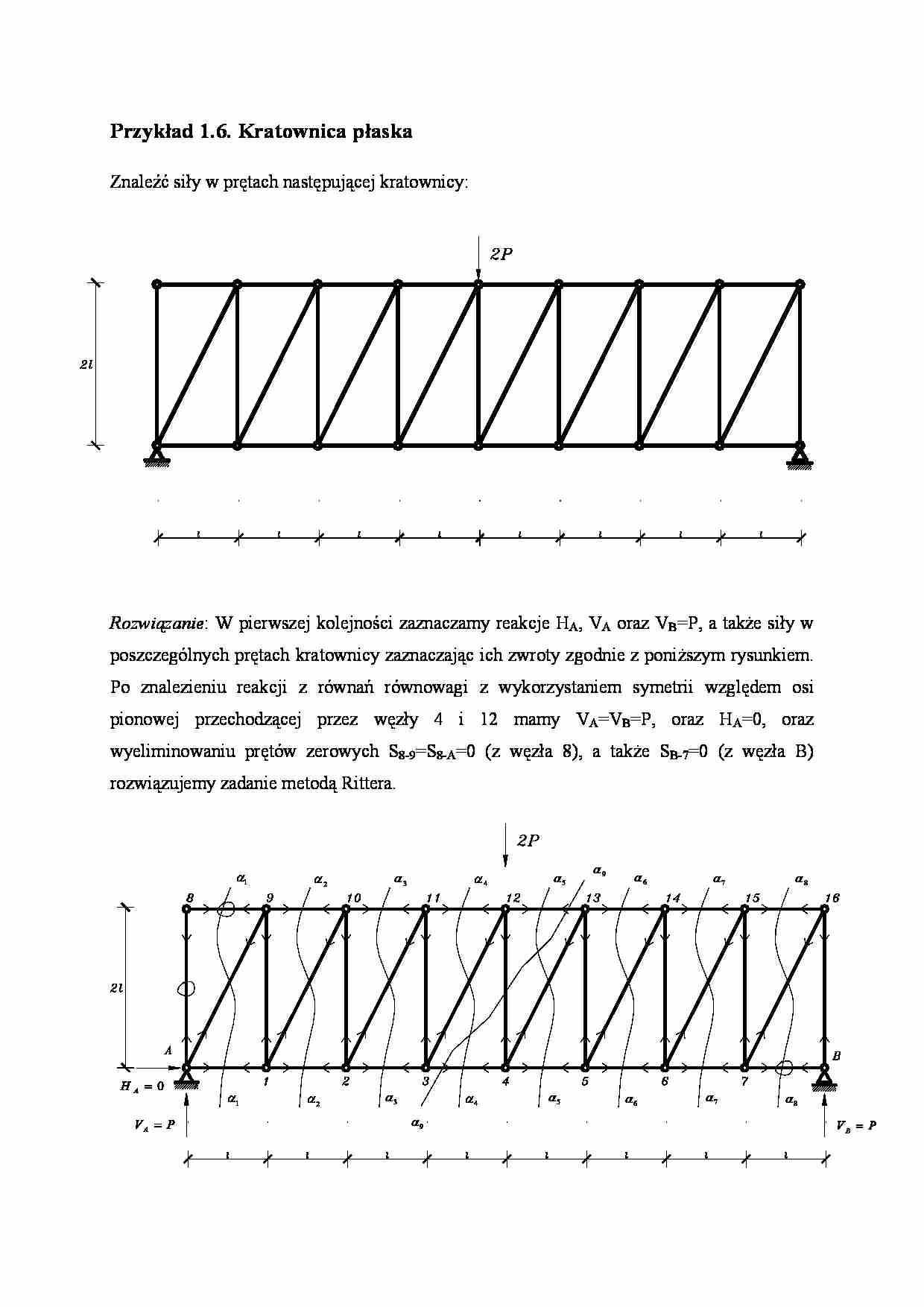

Przykład 1.6. Kratownica płaska Znaleźć siły w prętach następującej kratownicy: Rozwiązanie : W pierwszej kolejności zaznaczamy reakcje HA, VA oraz VB=P, a także siły w poszczególnych prętach kratownicy zaznaczając ich zwroty zgodnie z poniższym rysunkiem. Po znalezieniu reakcji z równań równowagi z wykorzystaniem symetrii względem osi pionowej przechodzącej przez węzły 4 i 12 mamy VA=VB=P, oraz HA=0, oraz wyeliminowaniu prętów zerowych S8-9=S8-A=0 (z węzła 8), a także SB-7=0 (z węzła B) rozwiązujemy zadanie metodą Rittera. 1 α 1 α 2 α 2 α 3 α 3 α 4 α 4 α 5 α 5 α 6 α 6 α 7 α 7 α 8 α 8 α 9 α 9 α 0 = A H P V A = P V B = W kolejnych przęsłach kratownicy stosujemy przekroje pionowe αi-αi dla i=1,…,9 oraz trzy równania równowagi 0 = ∑ − i i x P α α ; 0 = ∑ − i i y P α α ; 0 = ∑ − i i M α α dla mniejszej z odciętych części kratownicy otrzymujemy: • w przekroju α8-α8 (część prawa) 1. : 0 8 8 7 = ∑ − α α M 2 0 2 15 16 15 16 P S l S l B − = ⇒ = ⋅ + ⋅ − − V 2. : 0 8 8 = ∑ −α α y P P S S B 2 5 0 5 2 7 16 7 16 = ⇒ = − − − V • w przekroju α5-α5 (część prawa) 1. : 0 5 5 = ∑ −α α y P P S P S 2 5 0 5 2 4 13 4 13 = ⇒ = + ⋅ − − − 2. : 0 5 5 4 = ∑ − α α M P S l P l S 2 0 4 2 12 13 12 13 − = ⇒ = ⋅ + ⋅ − − 3. : 0 5 5 = ∑ −α α x P P 2 3 S 0 S S 5 1 S 4 5 4 5 4 13 12 13 = ⇒ = − − − − − − − • w przekroju α2-α2 (część lewa) 1. : 0 2 2 = ∑ −α α y P P S P S 2 5 0 5 2 10 1 10 1 − = ⇒ = + ⋅ − − 2. : 0 2 2 10 = ∑ − α α M P S Pl l S = ⇒ = − ⋅ − − 2 1 2 1 0 2 2 3. : 0 2 2 = ∑ −α α x P 2 0 5 1 9 10 1 10 1 2 9 10 P S S S S − = ⇒ = − − − − − − − W celu obliczenia siły w jednym ze słupków pionowych wykonujemy np. przekrój α9-α9 i znajdujemy dla części pionowej: 0 9 9 = ∑ −α α y P : P S P S − = ⇒ = + − − 12 4 12 4 0 . 2 Document Outline Przykład 1.6. Kratownica płaska
(…)
…, oraz HA=0, oraz
wyeliminowaniu prętów zerowych S8-9=S8-A=0 (z węzła 8), a także SB-7=0 (z węzła B)
rozwiązujemy zadanie metodą Rittera.
α9
α1 α2 α3 α4 α5 α6 α7 α8
H A =0
α1 α2 α3 α4 α5 α6 α7 α8
VA = P α9 VB = P
W kolejnych przęsłach kratownicy stosujemy przekroje pionowe αi-αi dla i=1,…,9 oraz trzy
równania równowagi ∑ Pα x
i −α i
= 0; ∑ Pα y
i −α i
= 0; ∑Mα i −α i
= 0 dla mniejszej z odciętych
części…
... zobacz całą notatkę




Komentarze użytkowników (0)