To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
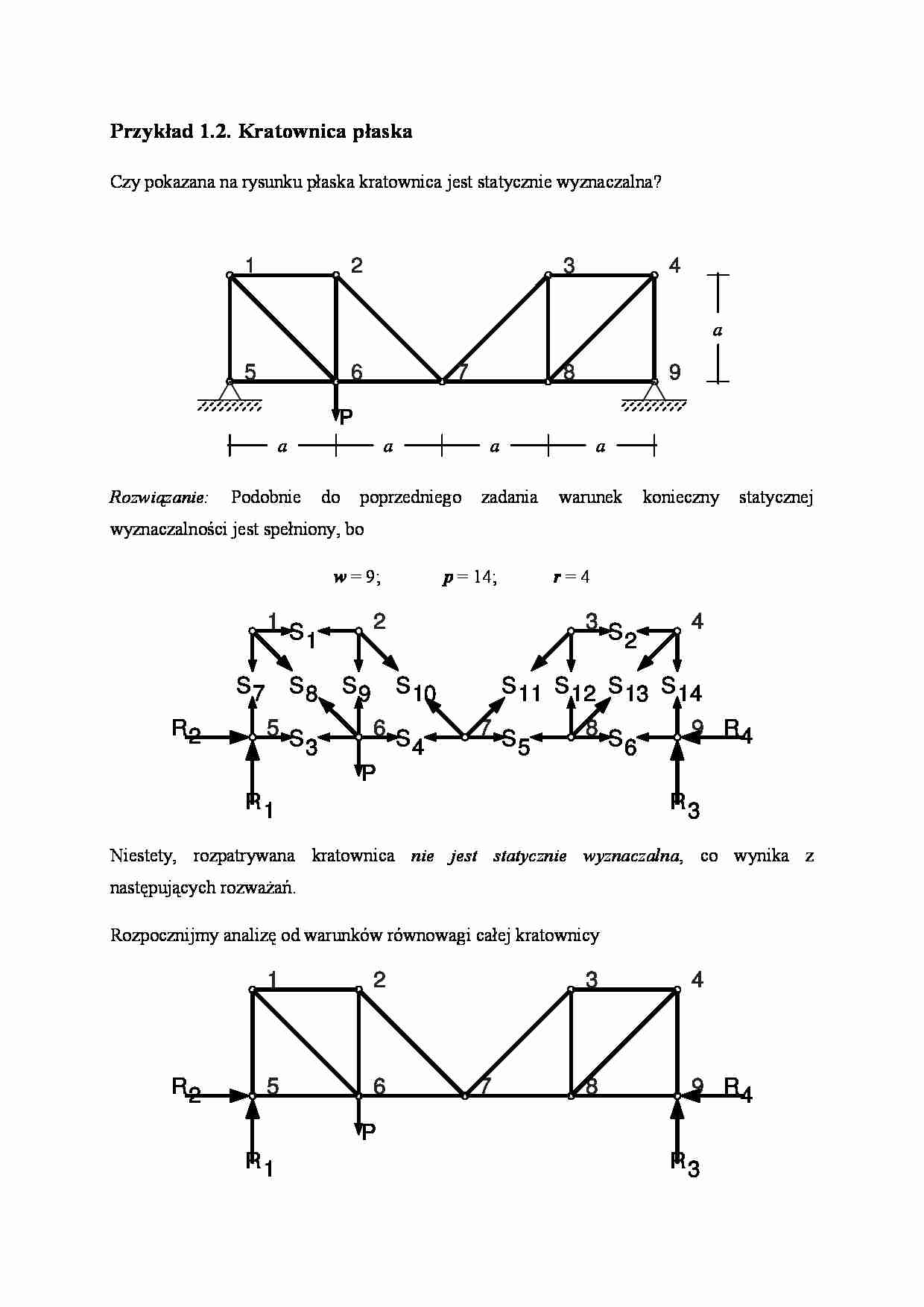

Przykład 1.2. Kratownica płaska Czy pokazana na rysunku płaska kratownica jest statycznie wyznaczalna? a a a a a P 9 8 7 6 5 4 3 2 1 w = 9; p = 14; r = 4 9 8 7 6 5 4 3 2 1 9 8 7 6 5 4 3 2 1 Rozwiązanie: Podobnie do poprzedniego zadania warunek konieczny statycznej wyznaczalności jest spełniony, bo 4 R 3 R 2 R 1 R 14 13 12 11 10 9 8 7 6 5 4 3 2 1 S S S S S S S S S S S S S S 13 12 11 10 9 8 7 6 5 4 3 2 1 S S S S S S S S S S S S S P Niestety, rozpatrywana kratownica nie jest statycznie wyznaczalna , co wynika z następujących rozważań. Rozpocznijmy analizę od warunków równowagi całej kratownicy 4 R 3 R 2 R 1 R P 0 5 = ∑ M ; 4 3 P R = ⇒ ; 0 9 = ∑ M ; 4 3 1 P R = ⇒ . Dla równowagi pokazanej części kratownicy 10 S 4 S 2 R 1 R P 7 6 5 2 1 powinno zachodzić 0 7 = ∑ M ; 0 2 2 1 = = − ⇒ Pa Pa a R ale nie zachodzi, bo P nie musi być zerem. 2 Document Outline Przykład 1.2. Kratownica płaska
... zobacz całą notatkę




Komentarze użytkowników (0)