Zadanie domowe-korelacja
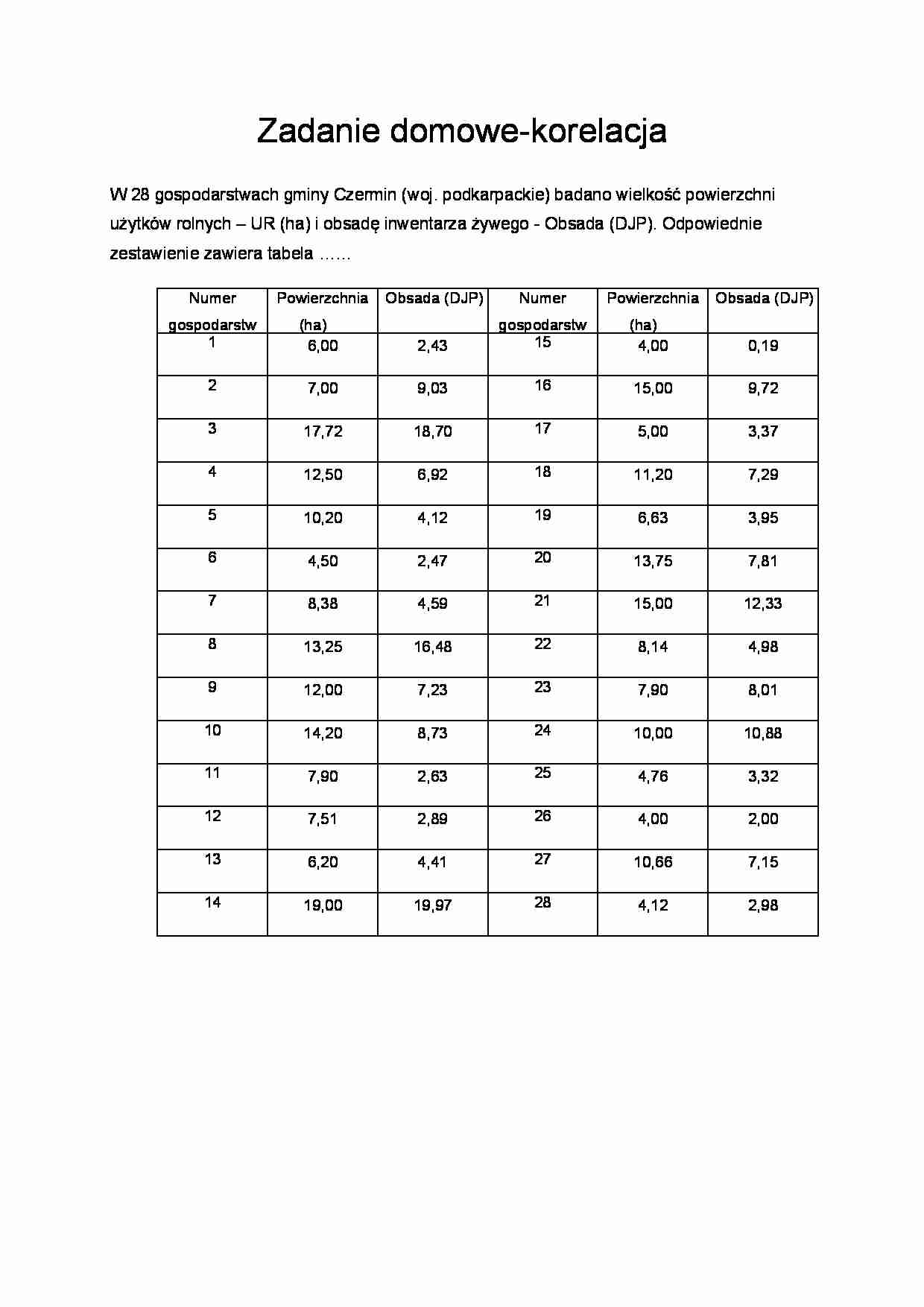
W 28 gospodarstwach gminy Czermin (woj. podkarpackie) badano wielkość powierzchni użytków rolnych - UR (ha) i obsadę inwentarza żywego - Obsada (DJP). Odpowiednie zestawienie zawiera tabela ……
Numer gospodarstwa
Powierzchnia (ha)
Obsada (DJP)
Numer gospodarstwa
Powierzchnia (ha)
Obsada (DJP)
1
6,00
2,43
15
4,00
0,19
2
7,00
9,03
16
15,00
9,72
3
17,72
18,70
17
5,00
3,37
4
12,50
6,92
18
11,20
7,29
5
10,20
4,12
19
6,63
3,95
6
4,50
2,47
20
13,75
7,81
7
8,38
4,59
21
15,00
12,33
8
13,25
16,48
22
8,14
4,98
9
12,00
7,23
23
7,90
8,01
10
14,20
8,73
24
10,00
10,88
11
7,90
2,63
25
4,76
3,32
12
7,51
2,89
26
4,00
2,00
13
6,20
4,41
27
10,66
7,15
14
19,00
19,97
28
4,12
2,98
Wykres funkcji regresji .
Korelacja to zależność dwóch zmiennych.
rxy=0,86 wysoka korelacja dodatnia tzn. że wraz ze wzrostem zmiennej x (obsada) rośnie średnia wartość zmiennej y (powierzchnia).
Korelacja umiarkowana czyli wartość bezwzględna współczynnika korelacji jest bliżej jedności i mieści się w przedziale (0,3;0,9)
Korelacja jest statystycznie istotna, co można udowodnić wykorzystując test współczynnika korelacji (bądź dokonać interpretacji wyników w programie Statistica):
-Na poziomie istotności -Ze względu na wysoki współczynnik korelacji można stwierdzić że korelacja jest statystycznie istotna
- stawiam hipotezę zerową i alternatywną:
n=28 H1: p=0 H2: p≠0 n-2=26-stopni swobody dla rozkładu t-Studenta (n<122-próba mała)
Wartość empiryczna(te) wynosi 8,7.
Dla n-2 stopni swobody przy poziomie istotności 0,05 odczytujemy z tablic rozkładu t-Studenta wartość: t 0,05;28 = 2,05, więc:
Odrzucamy hipotezę zerową, współczynnik korelacji Pearsona jest istotnie różny od 0 i jest statystycznie istotny-co należało udowodnić.
(…)
… zerową, współczynnik korelacji Pearsona jest istotnie różny od 0 i jest statystycznie istotny-co należało udowodnić.
Zmienną zależną jest powierzchnia, dlatego równanie regresji liniowej(prostej) będzie wyglądało następująco:
y= ax+b y- powierzchnia, x- obsada y= 0,7x+4,4
Współczynnik regresji liniowej wynosi 0,7 tzn. że jeżeli zmienna niezależna (obsada) wzrośnie o jednostkę to zmienna zależna…
... zobacz całą notatkę


Komentarze użytkowników (0)