To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
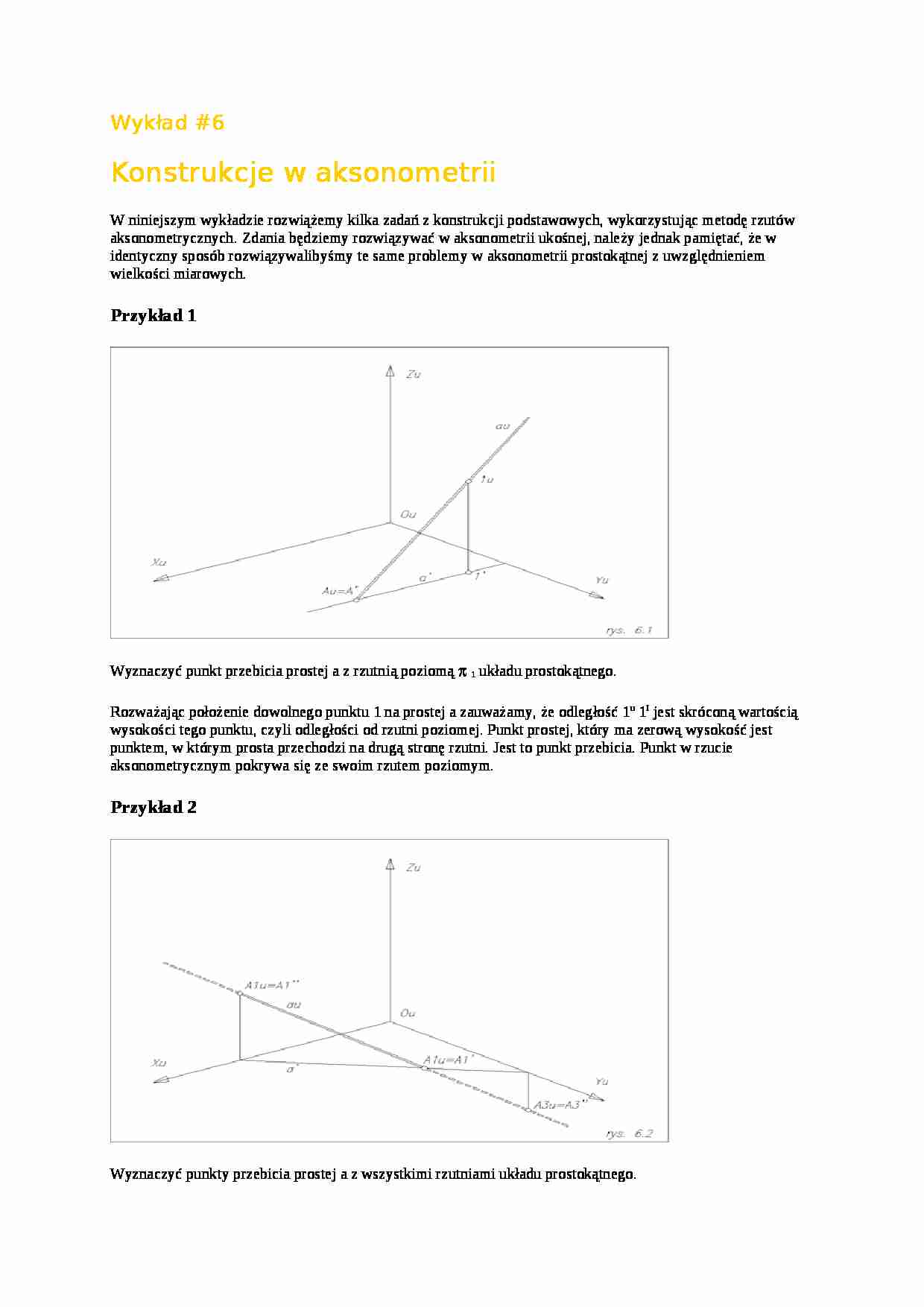


Wykład #6 Konstrukcje w aksonometrii W niniejszym wykładzie rozwiążemy kilka zadań z konstrukcji podstawowych, wykorzystując metodę rzutów aksonometrycznych. Zdania będziemy rozwiązywać w aksonometrii ukośnej, należy jednak pamiętać, że w identyczny sposób rozwiązywalibyśmy te same problemy w aksonometrii prostokątnej z uwzględnieniem wielkości miarowych. Przykład 1 Wyznaczyć punkt przebicia prostej a z rzutnią poziomą 1 układu prostokątnego. Rozważając położenie dowolnego punktu 1 na prostej a zauważamy, że odległość 1 u 1 I jest skróconą wartością wysokości tego punktu, czyli odległości od rzutni poziomej. Punkt prostej, który ma zerową wysokość jest punktem, w którym prosta przechodzi na drugą stronę rzutni. Jest to punkt przebicia. Punkt w rzucie aksonometrycznym pokrywa się ze swoim rzutem poziomym. Przykład 2 Wyznaczyć punkty przebicia prostej a z wszystkimi rzutniami układu prostokątnego. Punkt przebicia z rzutnią poziomą rozwiązujemy tak , jak w zadaniu poprzednim, leży on na przecięciu prostej w rzucie aksonometrycznym a u i rzutem prostej na rzutnię poziomą a I . Pu nkt prostej , którego rzut poziomy A 2 I przecina się z osią x ma zerową odległość od rzutni pionowej 2, a zatem jest to punkt przebicia prostej z tą rzutnią. Podobnie postępujemy szukając punktu przebicia z rzutnią trzecią ( boczną ). Przykład 3 Znaleźć krawędź pomiędzy płaszczyzną daną trzema punktami, a rzutnią poziomą 1 Przez dwa dowolne punkty prowadzimy prostą w rzucie aksonometrycznym i na rzutnię poziomą i dla każdej prostej szukamy punktu przebicia, jak w zadaniu poprzednim. Dwa punktu przebicia określą krawędź, trzeci punkt może być sprawdzeniem. Zakładamy, że rzutnie układu prostokątnego są nieprzeźroczyste, zatem krawędź będzie ograniczona osiami x i y Przykład 4 Określić krawędź płaszczyzny zadanej parą prostych równoległych a i b z rzutniami układu prostokątnego. Podobnie jak w zadaniu poprzednim wyznaczamy punkty przebicia prostych z rzutnią poziomą B 1 A 1, , wyznaczą one krawędź ograniczoną ze względu na widoczność osiami x i y. Punkty przecięcia K, L krawędzi z osiami są punktami należącymi jednocześnie do sąsiedniej rzutni i płaszczyzny a b. Oznacza to, że równocześnie są to punkty szukanych krawędzi z pozostałymi rzutniami . Podobnie, jak w przykładzie 2 znajdujemy punkty przebicia prostych z rzutniami pionową i boczną. Wraz z punktami L i K utworzą one pozostałe krawędzie. Pamiętajmy, że krawędzie płaszczyzny z rzutniami muszą spotykać się w punktach właściwych, lub niewłaściwych na osiach prostokątnego układu .
(…)
…, że krawędzie płaszczyzny z rzutniami muszą spotykać się w punktach właściwych, lub niewłaściwych na osiach prostokątnego układu .
Przykład 5 Wyznaczyć punkt przebicia pochyłego równoległoboku ABCD prostą l.
Przez prostą l w rzucie poziomym prowadzimy płaszczyznę pionową , wyznaczamy jej krawędź k z równoległobokiem Krawędź i prosta l leżą w tej samej płaszczyźnie , a zatem się przecinają, jest to punkt przebicia w którym prosta przechodzi na drugą stronę równoległoboku.
Przykład 6
Wyznaczyć krawędź pomiędzy trójkątem ABC , a zadanym prostopadłościanem.
Bok CB trójkąta i tylna ściana prostopadłościanu leżą w taj samej płaszczyźnie ( ich rzuty się pokrywają ) , więc w przestrzeni przecinają się w punktach 1 i 2 . Bok AC trójkąta i ściana boczna prostopadłościanu leżą na rzutni poziomej i przecinają…
… się w punktach 3 i 4. Łącząc odpowiednie punkty kierujemy się przynależnością punktów do tych samych ścian.
Przykład 7
Wyznaczyć punkty przebicia graniastosłupa prostą p
Stosujemy znany nam schemat postępowania z rzutów Monge`a. W dowolnym miejscu prostej p ( punkt 1 ) prowadzimy prostą w o wspólnym punkcie niewłaściwym (W ) zgodnym z kierunkiem krawędzi bocznych graniastosłupa. Proste p i w tworzą płaszczyznę…
... zobacz całą notatkę






Komentarze użytkowników (0)