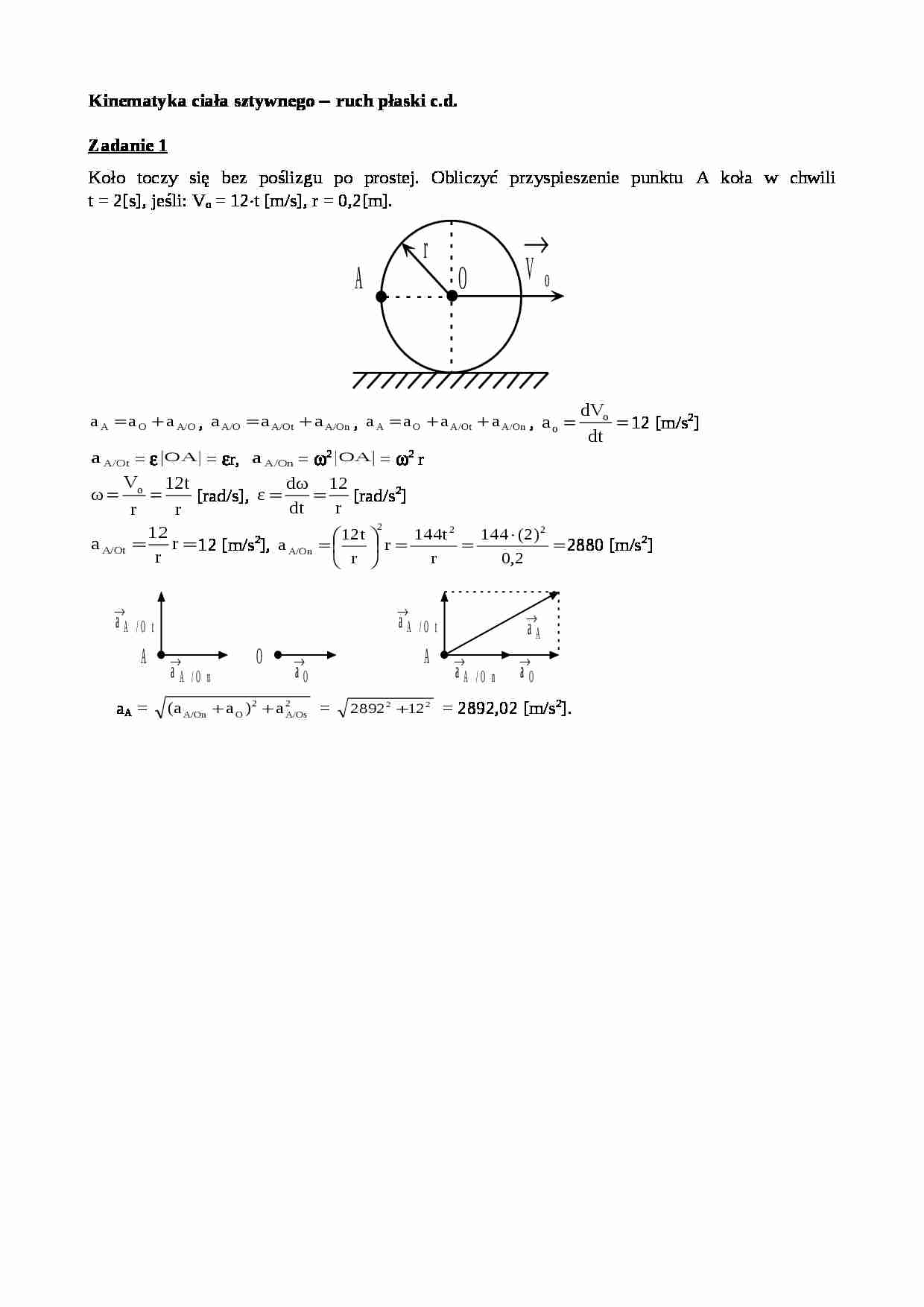
Kinematyka ciała sztywnego ruch płaski c.d. Zadanie 1 Koło toczy się bez poślizgu po prostej. Obliczyć przyspieszenie punktu A koła w chwili t = 2[s], jeśli: V o = 12t [m/s], r = 0,2[m].
, , , 12 [m/s 2 ]
= = r, = 2 = 2 r
[rad/s], [rad/s 2 ]
12 [m/s 2 ], 2880 [m/s 2 ]
a A = = = 2892,02 [m/s 2 ].
Zadanie 2 Koło zębate o promieniu R jest uruchamiane korbą OA obracającą się dokoła osi O stałego koła zębatego o tym samym promieniu. Korba obraca się z prędkością kątową stałą o . Wyznaczyć przyspieszenie punktu koła ruchomego, który w danej chwili jest chwilowym środkiem obrotu tego koła.
Po wyprowadzeniu wzoru ogólnego wykonać obliczenia dla: R = 12[cm], o = 2[rad/s].
prędkość kątowa koła ruchomego.
Chwilowym środkiem obrotu koła ruchomego jest punkt C styku obydwu kół (V C = 0)
, , Punkt A porusza się po okręgu o promieniu 2R. Wobec tego:
, = o R = 0, bo o 0 ( o jest stała), = 2R czyli: = 2 R
→ = 2 = 2 R , = = R , = ?, = ?
Dla korby OA prędkość punktu A: V A = o 2R
Chwilowym środkiem obrotu koła ruchomego jest punkt C, zatem: Prędkość punktu A: V A = = R
Wobec tego: o 2R = R → = 2 o , 0, (bo jest stała)
= 2 R = (2 o ) 2 R = 4 R
a c = a C/A a A = 4 R 2 R = 2 R, R = 12 [cm] = 0,12 [m], o = 2 [rad/s].
czyli: a c = 0,96 [m/s 2 ].
Zadanie 3 Pręt prosty AB ślizga się ruchem płaskim po osiach układu Oxy. W chwili, gdy tworzy on z osią Ox kąt = 60 o , prędkość jego końca A wynosi V A = 2[m/s]. Wyznacz dla tego położenia chwilowy środek obrotu, prędkość kątową pręta i prędkość końca B.
Oznaczmy długość pręta AB jako l i przyjmijmy jego długość l = 1[m] będzie ona potrzebna do obliczenia prędkości kątowej (ω) pręta.
Punkt C jest chwilowym środkiem obrotu pręta AB (V C = 0)
, ale , czyli: → Podstawiając dane liczbowe otrzymujemy: , stąd: Podstawiając dane liczbowe otrzymujemy: .
Zadanie 4 Przyspieszenia końców pewnego pręta prostego wynoszą a A i a B . Wyznaczyć przyspieszenie a S środka S tego pręta, oznaczyć na rysunku jego kierunek i zwrot oraz obliczyć wartość przyspieszenia a S , jeśli: a A = a B = [m/s 2 ].
, , , , z rysunku widać, że: , czyli możemy zapisać:
(…)
… się na szpulę. Dane: a, b, e, u.
Punkt C jest chwilowym środkiem obrotu (VC = 0)
VB = VA = u, , W jednakowym czasie t droga środka szpuli (so) O musi być o e większa od drogi punktów B (sA) (leżących stale pod punktem O):
so = sB + e (1)
Oba punkty poruszają się ruchem jednostajnym, zatem ich drogi wynoszą:
so = Vot , sA = ut
stąd i po podstawieniu do wzoru (1) otrzymujemy
stąd: , a po uwzględnieniu wzoru…
… (Vb) punktu (oznaczyliśmy go jako A) wyznaczamy ze wzoru:
, gdzie: Vw prędkość względna, Vu prędkość unoszenia
W rozpatrywanym przypadku ruch względny jest ruchem postępowym, prostoliniowym, wobec tego prędkość względna punktu A dana jest wzorem:
Prędkość unoszenia wyznaczamy ze wzoru:
gdzie jest wektorem poprowadzonym ze środka koła do punktu A
Długość wektora jest równa…
… na poniższym rysunku.
Z rysunku widać, że: [m/s2].
Zadanie 7
Linia kolejowa przebiega wzdłuż południka. Lokomotywa jedzie z prędkością V = 180 [km/h] na południe. Obliczyć przyspieszenie Coriolisa lokomotywy w chwili, gdy jej położenie jest określone szerokością geograficzną północną = 60o.
, , wobec tego:
, V = 50 [m/s]
, T okres obrotu Ziemi dookoła własnej osi, T= 24 [h] = 86400 [s…
... zobacz całą notatkę





Komentarze użytkowników (0)