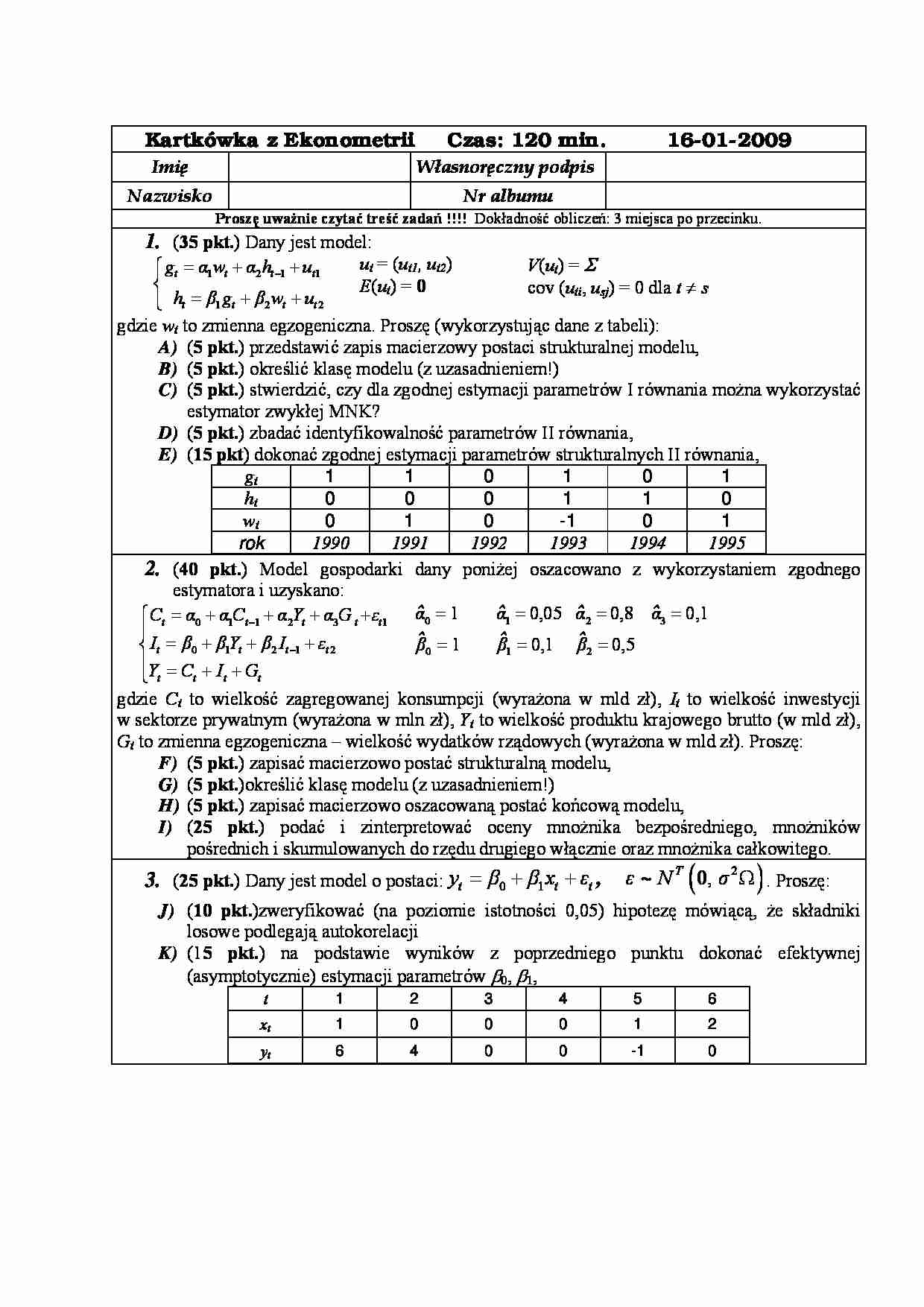
Kartkówka z Ekonometrii Czas: 120 min. 16-01-2009 Imię Własnoręczny podpis Nazwisko Nr albumu Proszę uważnie czytać treść zadań !!!! Dokładność obliczeń: 3 miejsca po przecinku. 1. ( 35 pkt. ) Dany jest model: ut = ( ut1, ut2 ) V ( ut ) = Σ E ( ut ) = 0 cov ( uti , usj ) = 0 dla t ≠ s gdzie wt to zmienna egzogeniczna. Proszę (wykorzystując dane z tabeli): A) ( 5 pkt. ) przedstawić zapis macierzowy postaci strukturalnej modelu, B) ( 5 pkt. ) określić klasę modelu (z uzasadnieniem!) C) ( 5 pkt. ) stwierdzić, czy dla zgodnej estymacji parametrów I równania można wykorzystać estymator zwykłej MNK? D) ( 5 pkt. ) zbadać identyfikowalność parametrów II równania, E) ( 15 pkt ) dokonać zgodnej estymacji parametrów strukturalnych II równania, gt 1 1 0 1 0 1 ht 0 0 0 1 1 0 wt 0 1 0 -1 0 1 rok 1990 1991 1992 1993 1994 1995 2. ( 40 pkt. ) Model gospodarki dany poniżej oszacowano z wykorzystaniem zgodnego estymatora i uzyskano: 0 1 1 2 3 1 0 1 2 1 2 t t t t t t t t t t t t t C α α C α Y α G ε I β β Y β I ε Y C I G − − = + + + + ⎧ ⎪ = + + + ⎨ ⎪ = + + ⎩ 0 ˆ α = 1 0,05 0,8 3 ˆ α = 0 ˆ 0,1 1 0,1 0,5 gdzie Ct to wielkość zagregowanej konsumpcji (wyrażona w mld zł), It to wielkość inwestycji w sektorze prywatnym (wyrażona w mln zł), Yt to wielkość produktu krajowego brutto (w mld zł), Gt to zmienna egzogeniczna – wielkość wydatków rządowych (wyrażona w mld zł). Proszę: F) ( 5 pkt. ) zapisać macierzowo postać strukturalną modelu, G) ( 5 pkt. )określić klasę modelu (z uzasadnieniem!) H) ( 5 pkt. ) zapisać macierzowo oszacowaną postać końcową modelu, I) ( 25 pkt. ) podać i zinterpretować oceny mnożnika bezpośredniego, mnożników pośrednich i skumulowanych do rzędu drugiego włącznie oraz mnożnika całkowitego. 3. ( 25 pkt. ) Dany jest model o postaci: ( ) 2 0 1 , Ω , ~ T t t t y β β x ε ε N σ = + + 0 . Proszę: J) ( 10 pkt. )zweryfikować (na poziomie istotności 0,05) hipotezę mówiącą, że składniki losowe podlegają autokorelacji K) (1 5 pkt. ) na podstawie wyników z poprzedniego punktu dokonać efektywnej (asymptotycznie) estymacji parametrów β0, β1, t 1 2 3 4 5 6 xt 1 0 0 0 1 2 yt 6 4 0 0 -1 0 1 2 1 1 1 2 2 t t t t t t t t g α w α h u h β g β w u − = + + ⎧⎪
... zobacz całą notatkę



Komentarze użytkowników (0)