To tylko jedna z 19 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Ruch krytyczny (critical flow, kritische Strömung)
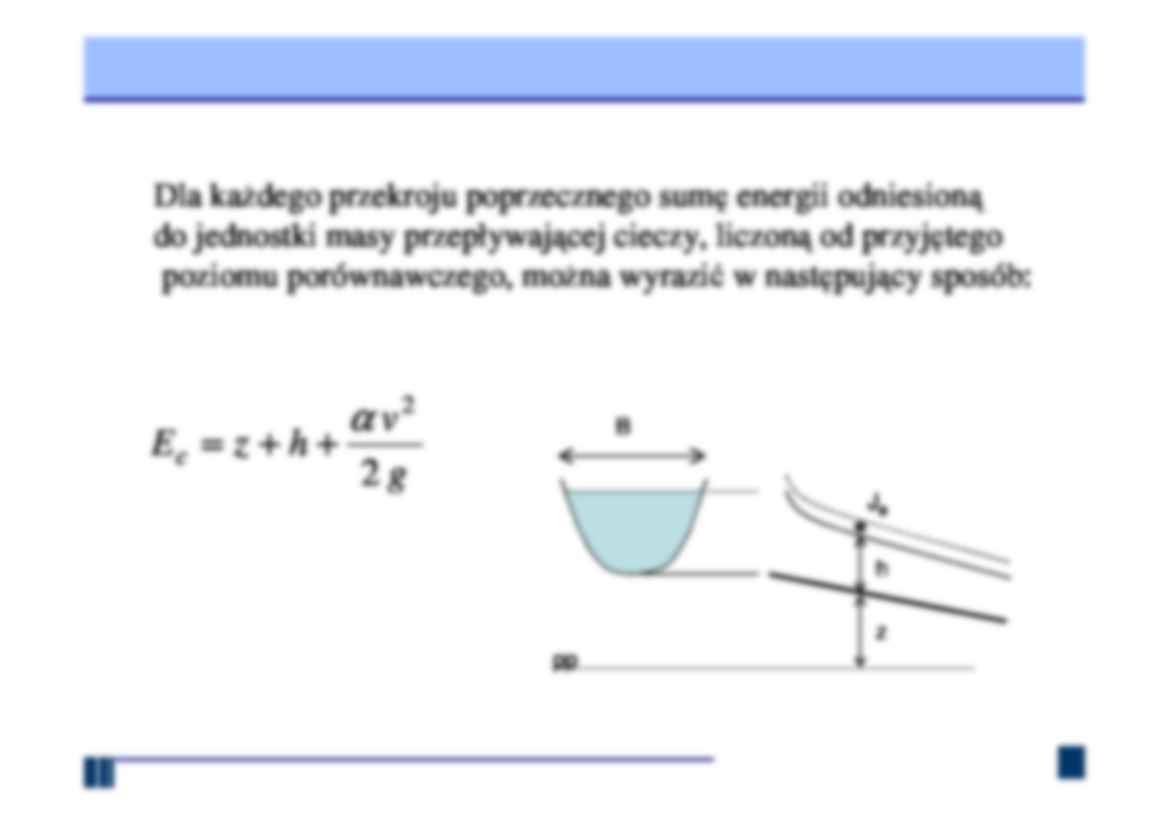
Dla kaŜdego przekroju poprzecznego sumę energii odniesioną
do jednostki masy przepływającej cieczy, liczoną od przyjętego
poziomu porównawczego, moŜna wyrazić w następujący sposób:
Ec = z + h +
α v2
B
2g
Je
h
z
pp
B
Ec = z + h +
α v2
Je
2g
h
z
pp
Wysokość połoŜenia z jest dla danego koryta dla kaŜdego przekroju stała,
i niezaleŜna od warunków przepływu.
Dla danego koryta parametry hydrodynamiczne: głębokość i prędkość (h i v),
czyli pole przekroju poprzecznego i wydatek (A i Q) mogą przybierać róŜne wartości.
Dlatego teŜ w wielu przypadkach korzystnym jest ograniczenie analizy
do sumy energii tych wielkości zmiennych, określonych wyraŜeniem:
E=h+
α v2
2g
= Ec = h +
α Q2
2 g A2
E=h+
α v2
2g
= Ec = h +
α Q2
2 g A2
ZałóŜmy, Ŝe przepływ jest stały Q = const,
wtedy zmienność energii opisuje funkcja jednej
zmiennej niezaleŜnej h, E = E(h).
Przebieg zmienności tej funkcji jest następujący:
gdy h → 0 to A → 0, stąd E → ∞
gdy h → ∞ to A → ∞, stąd E → ∞
Głębokość wody h jest wielkością,
która moŜe przybierać tylko wartości dodatnie,
czyli z powyŜszej analizy wynika,
Ŝe musi występować minimum badanej funkcji E(h).
Warunkiem wystąpienia ekstremum funkcji energii jest
zerowanie pierwszej pochodnej:
dE
α Q2 d A
=1−
=0
3
dh
gA dh
poniewaŜ zachodzi zaleŜność dA = B dh, to ostatecznie warunek
występowania ekstremum (minimum) badanej funkcji przybiera postać:
3
A
=
B
α Q2
g
Głębokość która spełnia podane równanie
i przy której występuje minimum funkcji E(h)
nazywana jest głębokością krytyczną hkr.
(critical depth, kritische Tiefe)
Przepływ przy większych głębokościach a
więc i przy mniejszych prędkościach nazywany
jest ruchem spokojnym (subcritical flow, unterkritische
Strömung), ruch odbywający się przy mniejszych
głębokościach jednak przy większych
prędkościach nazywany jest ruchem rwącym
(supercritical flow, überkritische Strömung).
Ruchem krytycznym nazywamy taki ruch,
w którym przy stałym przepływie energia
strumienia osiąga wartość minimalną
lub przy stałej energii strumienia przepływ
osiąga maksimum.
W obliczeniach praktycznych często wygodnie jest
posługiwać się pojęciem głębokości średniej,
która jest ilorazem pola przekroju poprzecznego i
szerokości koryta w zwierciadle wody:
hśr = A / B.
W przypadku koryta o przekroju prostokątnym,
głębokość średnia jest rzeczywistą głębokością
napełnienia koryta.
Po wprowadzeniu do równania ruchu krytycznego
wyŜej zdefiniowanej głębokości średniej,
równanie to moŜna sprowadzić do następujących postaci:
2
hkr = 3
Q
,
2
gB
vkr =
g hkr
Rodzaj ruchu tzn. czy jest to ruch krytyczny, rwący czy
spokojny w dogodny sposób opisuje bezwymiarowa liczba Froude`a
(Froude number, Froud-Zahl):
Fr =
v
gh
Gdy prędkość przepływającej wody jest prędkością krytyczną,
to licznik jest równy mianownikowi czyli
liczba Froude`a jest równa jedności co wynika
wprost z równania ruchu krytycznego, stąd gdy:
Fr = 1 jest to ruch krytyczny
Fr 1 ruch
(…)
… czyli
liczba Froude`a jest równa jedności co wynika
wprost z równania ruchu krytycznego, stąd gdy:
Fr = 1 jest to ruch krytyczny
Fr > 1 ruch rwący
Fr < 1 ruch spokojny
Na długich odcinkach koryta występuje z reguły ruch jednostajny,
tzn. stan swego rodzaju równowagi zasobów energii danego cieku
i strat energii wywołanych ruchem cieczy –
straty energii na opory ruchu są równe róŜnicy
poziomu dna cieku…
…. Zmiana charakteru przepływu
z ruchu spokojnego w ruch rwący przebiega łagodnie,
głębokości stopniowo maleją a prędkości stopniowo
zwiększają się przybierając wartości krytyczne mniej
więcej na granicy tych dwóch odcinków koryta.
Odmiennie przebiega zmiana ruchu rwącego w ruch spokojny.
W tym przypadku przejście jest gwałtowne,
i towarzyszy mu zjawisko powstawania odskoku hydraulicznego
(hydraulic jump…
... zobacz całą notatkę






Komentarze użytkowników (0)