To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Adam Zaborski. Wytrzymałosc materiałów, semestr 1
Walerowicz Paweł WIL gr. 9
Projekt nr 1
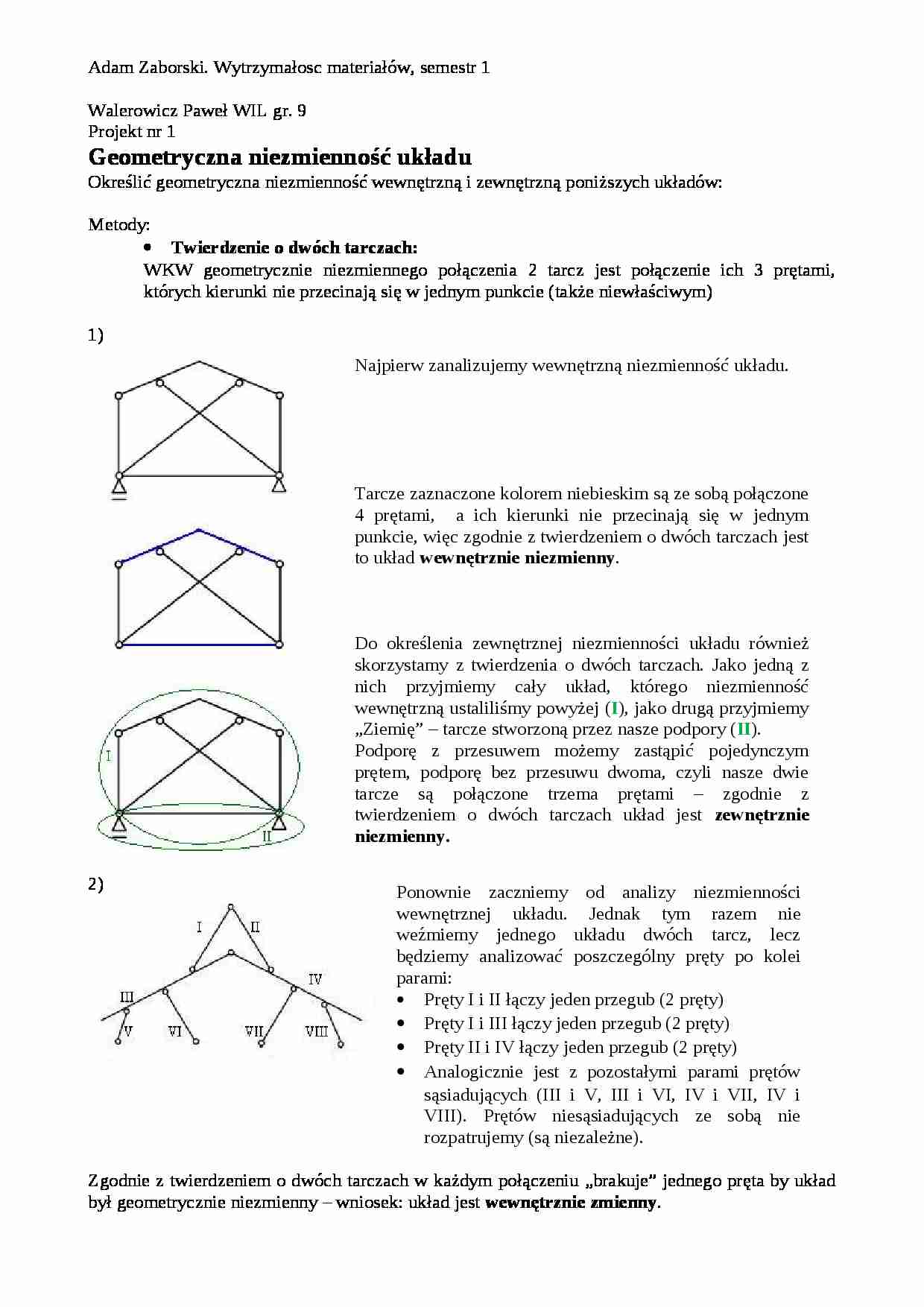
Geometryczna niezmienno ść układu Określić geometryczna niezmienność wewnętrzną i zewnętrzną poniższych układów: Metody:
Twierdzenie o dwóch tarczach: WKW geometrycznie niezmiennego połączenia 2 tarcz jest połączenie ich 3 prętami, których kierunki nie przecinają się w jednym punkcie ( także niewłaściwym )
1)
2)
Zgodnie z twierdzeniem o dwóch tarczach w każdym połączeniu „brakuje” jednego pręta by układ był geometrycznie niezmienny - wniosek: układ jest wewnętrznie zmienny .
Niestety, z twierdzenia o dwóch tarczach nie jesteśmy w stanie wyciągnąć konkluzji na temat niezmienności tego układu.
3)
Twierdzenie o trzech tarczach: WKW geometrycznie niezmiennego połączenia 3 tarcz jest połączenie ich (każda z każdą) dwoma prętami, których kierunki nie przecinają się w punktach leżących na jednej prostej (2 z tych punktów mogą być niewłaściwe ) 1) 2) Zostaje nam tylko sprawdzenie zmienności uwzględniając pręty A i B. Jeżeli jako dwie tarczę przyjmiemy A i B a jako trzecią układ, który przed chwilą określiliśmy jako geometrycznie niezmienny widzimy, że wszystkie te tarcze połączone są przegubami, które zamieniając parami prętów pokazują nam, zgodnie z twierdzeniem o trzech tarczach, że układ jest zewnętrznie niezmienny . 3) Plan prędkości wirtualnych: rysunek możliwych (z uwagi na nałożone więzy) prędkości; jeśli istnieje niesprzeczny plan takich prędkości to układ jest geometrycznie niezmienny. 1)
2)
3)
Podsumowanie:
Każdy z przykładów obliczony na trzy sposoby dał te same wnioski dotyczące niezmienności.
Najpierw zanalizujemy wewnętrzną niezmienność układu.
... zobacz całą notatkę






Komentarze użytkowników (1)
john napisał(a):
2016-10-26 18:01:05
Co to k****a jest "WKW"???