Fizyka - Rozkład normalny

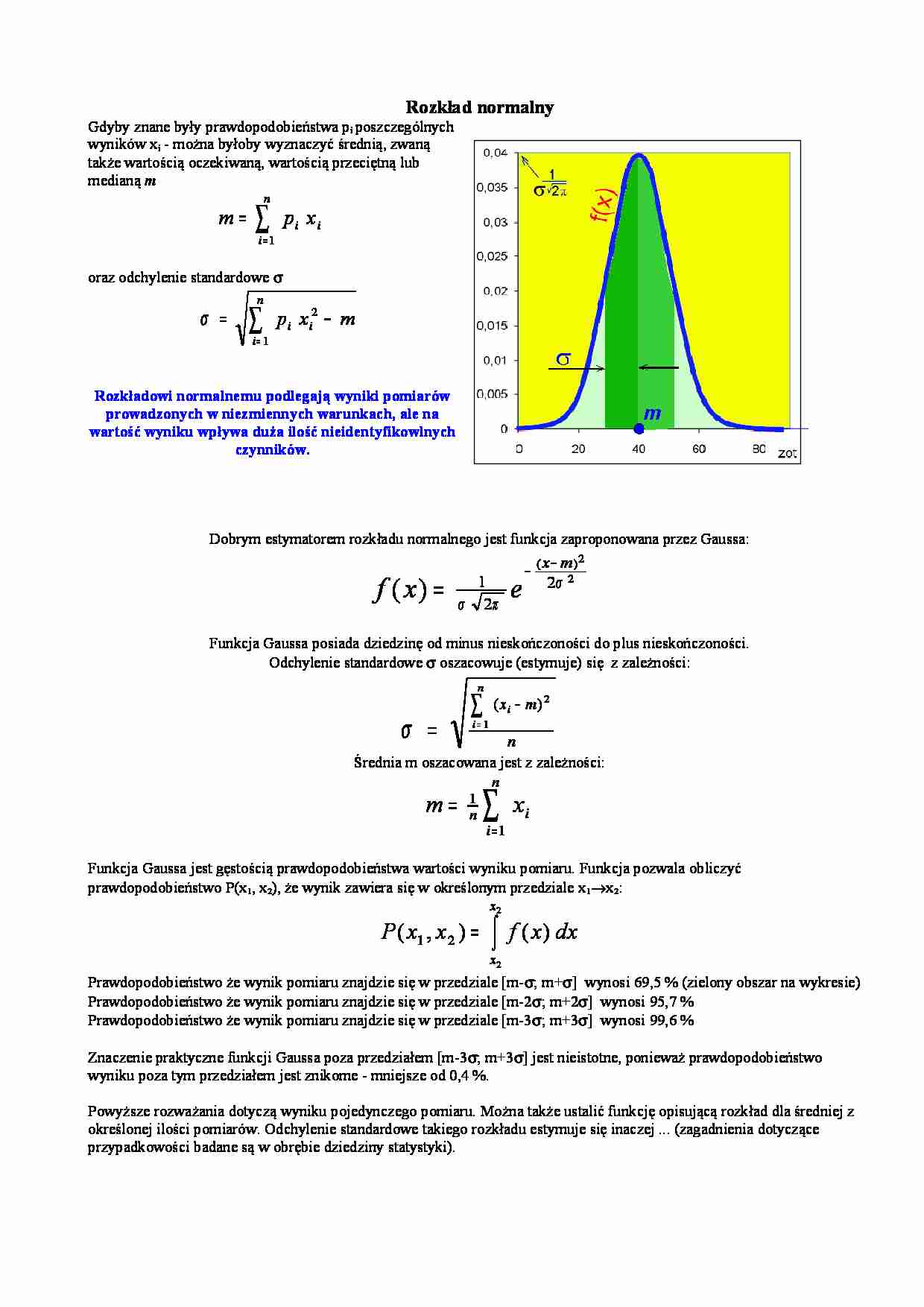
Rozkład normalny Gdyby znane były prawdopodobieństwa pi poszczególnych  wyników xi - można byłoby wyznaczyć średnią, zwaną  także wartością oczekiwaną, wartością przeciętną lub  medianą  m ∑ = = n i i i x p m 1 oraz odchylenie standardowe  σ ∑ = − = n i i i m x p 1 2 σ Rozkładowi normalnemu podlegają wyniki pomiarów  prowadzonych w niezmiennych warunkach, ale na  wartość wyniku wpływa duża ilość nieidentyfikowlnych  czynników. Dobrym estymatorem rozkładu normalnego jest funkcja zaproponowana przez Gaussa: 2 2 ) ( 2 2 1 ) ( σ π σ m x e x f − − = Funkcja Gaussa posiada dziedzinę od minus nieskończoności do plus nieskończoności. Odchylenie standardowe  σ oszacowuje (estymuje) się  z zależności: n m x n i i ∑ = = − 1 2 ) ( σ Średnia m oszacowana jest z zależności: ∑ = = n i i n x m 1 1 Funkcja Gaussa jest gęstością prawdopodobieństwa wartości wyniku pomiaru. Funkcja pozwala obliczyć  prawdopodobieństwo P(x1, x2), że wynik zawiera się w określonym przedziale x1 →x2: ∫ = 2 2 ) ( ) , ( 2 1 x x dx x f x x P Prawdopodobieństwo że wynik pomiaru znajdzie się w przedziale [m- σ; m+σ]  wynosi 69,5 % (zielony obszar na wykresie) Prawdopodobieństwo że wynik pomiaru znajdzie się w przedziale [m-2 σ; m+2σ]  wynosi 95,7 % Prawdopodobieństwo że wynik pomiaru znajdzie się w przedziale [m-3 σ; m+3σ]  wynosi 99,6 % Znaczenie praktyczne funkcji Gaussa poza przedziałem [m-3 σ; m+3σ] jest nieistotne, ponieważ prawdopodobieństwo  wyniku poza tym przedziałem jest znikome - mniejsze od 0,4 %.  Powyższe rozważania dotyczą wyniku pojedynczego pomiaru. Można także ustalić funkcję opisującą rozkład dla średniej z  określonej ilości pomiarów. Odchylenie standardowe takiego rozkładu estymuje się inaczej ... (zagadnienia dotyczące  przypadkowości badane są w obrębie dziedziny statystyki).   Document Outline Rozkład normalny ... zobacz całą notatkę