To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

67. Fonony: fale sprężyste w krysztale w zakresie fal krótkich. Napisz równanie ruchu fal sprężystych w krysztale. Zdefiniuj strefy Brillouina dla fononów. Fonony to kwanty energii fali sprężystej. Fale dźwiękowe w kryształach złożone są z fononów. Drgania termiczne w kryształach są to termicznie wzbudzone fonony. Fonony są bozonami i podlegają statystyce Bosego - Einsteina.
Długość fal sprężystych w krysztale w zakresie fal krótkich jest porównywalna ze stałą sieci. Rozważmy fale rozchodzące się w kierunkach, dla których są one spolaryzowane poprzecznie lub podłużnie. Podczas rozchodzenia się fali, cała płaszczyzna zostaje przesunięta prostopadle lub równolegle do wektora falowego k, wówczas przesunięcie z położenia równowagi jest opisane współrzędną u.
Zakładamy, że siła działająca na płaszczyznę s wywołana przez przesunięcie płaszczyzny oznaczonej przez s+p jest proporcjonalna do różnicy ich przesunięć i wówczas całkowitą siłę działającą na płaszczyznę s można zgodnie z prawem Hooka wyrazić:
gdzie: jest współczynnikiem siły działającej między płaszczyznami przesuniętymi o p
F oraz są przyporządkowane jednemu atomowi w płaszczyźnie.
Równanie ruchu ma więc postać:
Rozwiązaniem tego równania jest fala bieżąca:
gdzie a jest odległością między płaszczyznami, k wektorem falowym
Po podstawieniu (IV-8) do (IV-7) otrzymamy:
Z równana (IV-9) wynika specyficzna zależność częstości fali ( fononu) od wektora falowego, która nosi nazwę dyspersji:
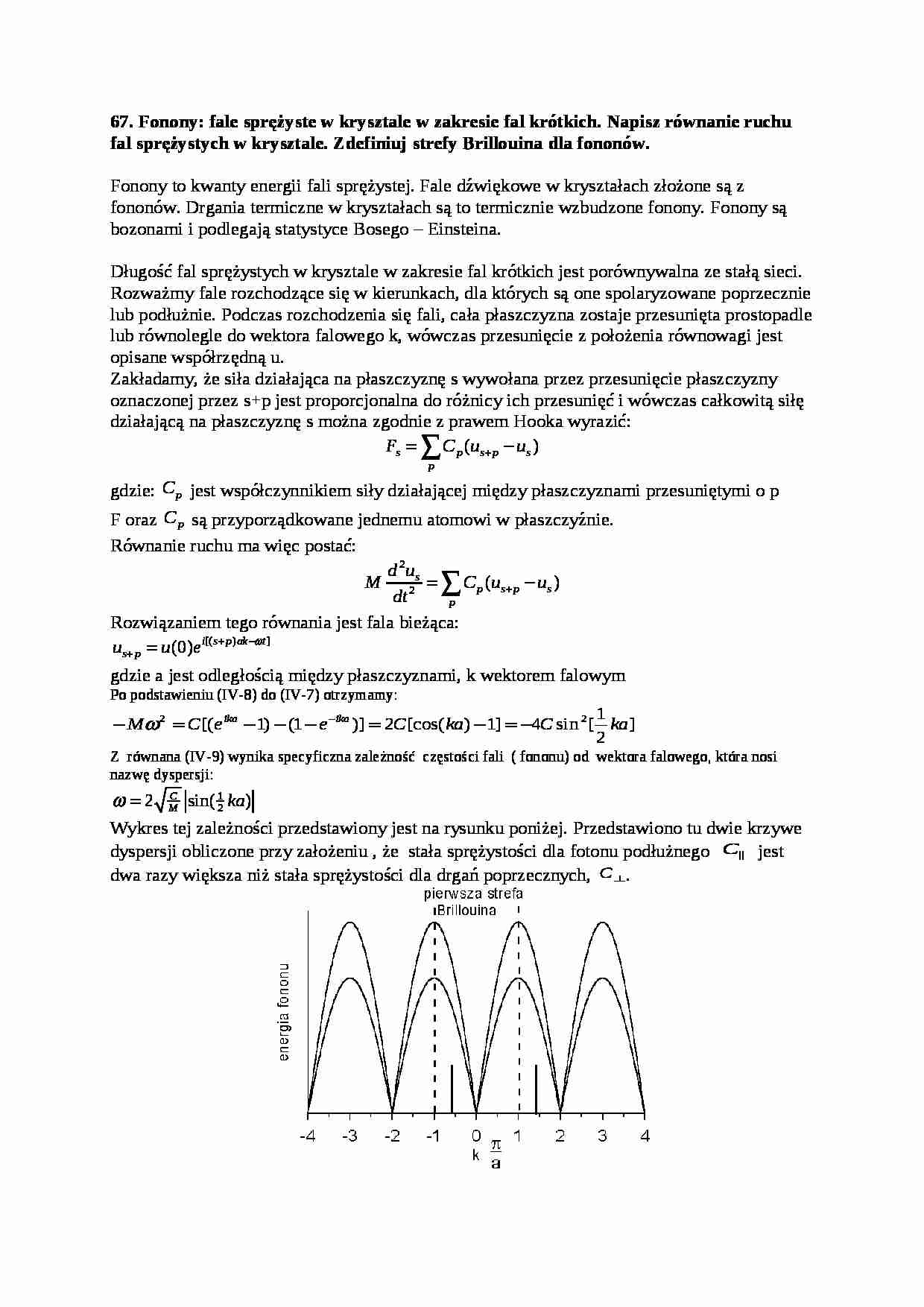
Wykres tej zależności przedstawiony jest na rysunku poniżej. Przedstawiono tu dwie krzywe dyspersji obliczone przy założeniu , że stała sprężystości dla fotonu podłużnego jest dwa razy większa niż stała sprężystości dla drgań poprzecznych, . Strefy Brillouina:
Daje się zauważyć, że krzywa dyspersji jest funkcją periodyczną z okresem . W ogólnym przypadku funkcja dyspersji jest periodyczna z okresem sieci odwrotnej. Powracając do definicji pierwszej strefy Brillouina, w przypadku naszych drgań odpowiada ona odcinkowi ( , ). Jak widać, ze względu na periodyczność wszystkie informacje o własnościach fononów znajdują się w obszarze pierwszej strefy Brillouina. Powyższy wniosek pozostaje słuszny również dla bardziej skomplikowanych struktur. Warto zastanowić się nad sensem fizycznym powyższych prawidłowości. Zastanówmy się co wynika z zależności wektora falowego od długości fali, . Jeśli k byłoby poza zakresem pierwszej strefy Brillouina, to odpowiadająca mu długość fali byłaby mniejsza niż 2 stałe sieci. Praktycznie w krysztale fale takie nie mogą istnieć, a jeśli mimo wszystko założymy, że istnieją to ruch atomów, czyli to co obserwujemy byłby taki jak dla fali o większej długości. Np. fala, poruszająca się w kierunku (+x), o wektorze falowym
(…)
… wektora falowego wynika, że obserwowany ruch odpowiadałby fali poruszającej się w kierunku przeciwnym (-x). Sytuacja gdy wektor falowy odpowiada fali stojącej w krysztale. Zauważamy, że zakres możliwych energii fononów jest ograniczony. Z rysunku wynika ,że zmienia się on od 0 do . Zakres dozwolonych energii określany jest często jako widmo fononów.
…
... zobacz całą notatkę




Komentarze użytkowników (0)