To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
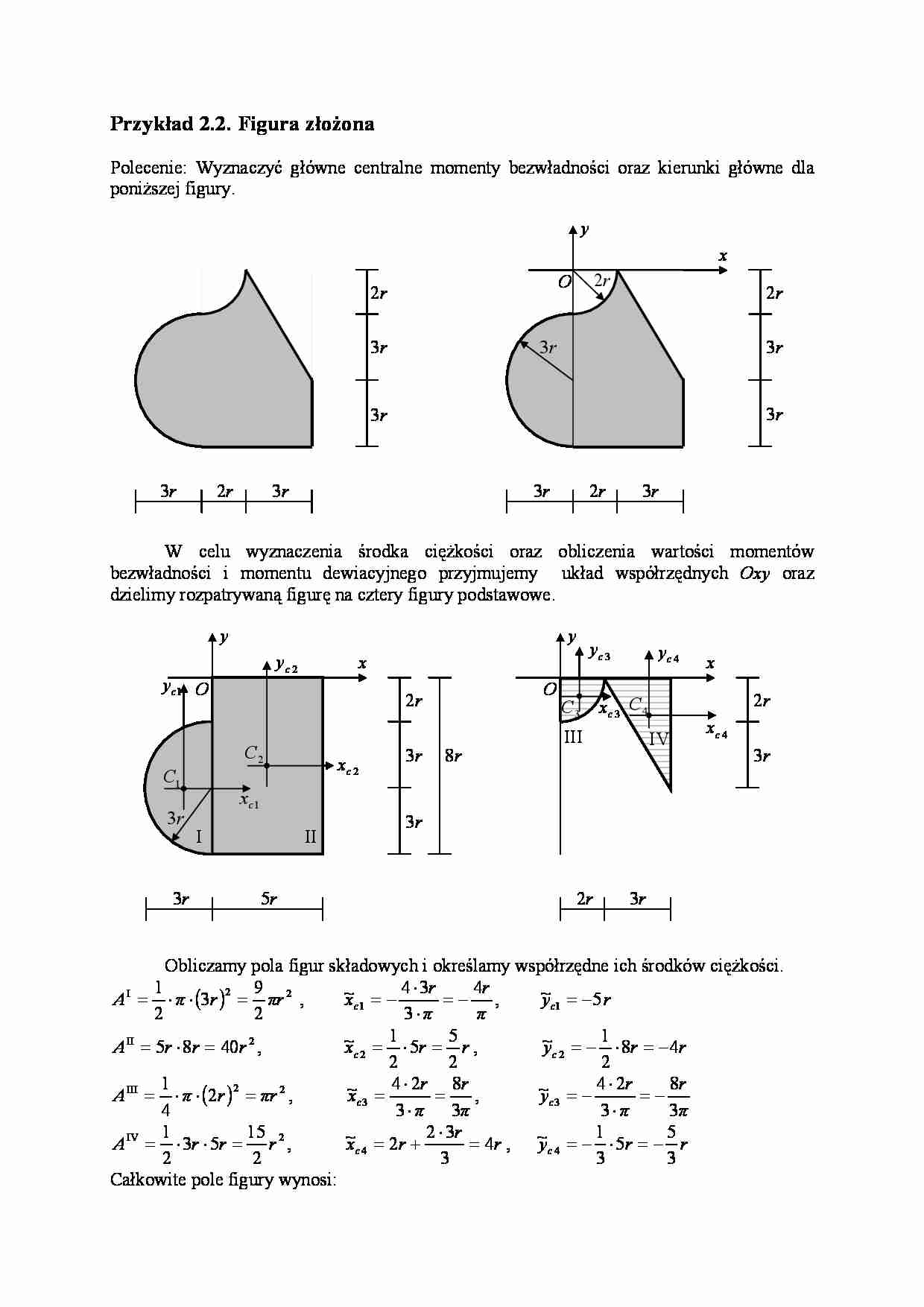


Przykład 2.2. Figura złożona
Polecenie: Wyznaczyć główne centralne momenty bezwładności oraz kierunki główne dla
poniższej figury.
y
x
2r
O
2r
2r
3r
3r
3r
3r
3r
3r
2r
3r
2r
3r
3r
W celu wyznaczenia środka ciężkości oraz obliczenia wartości momentów
bezwładności i momentu dewiacyjnego przyjmujemy układ współrzędnych Oxy oraz
dzielimy rozpatrywaną figurę na cztery figury podstawowe.
y
y
yc 2
yc1 O
3r
3r
O
2r
C2
C1
yc 3
x
xc 2
3r
8r
C3
yc 4
2r
xc 3 C 4
III
x
IV
xc 4
3r
xc 1
I
II
5r
3r
2r
3r
Obliczamy pola figur składowych i określamy współrzędne ich środków ciężkości.
1
9
2
~ = − 4 ⋅ 3r = − 4r ,
~ = −5 r
A I = ⋅ π ⋅ (3r ) = πr 2 ,
xc 1
y c1
2
2
π
3⋅π
~ = 1 ⋅ 5r = 5 r ,
~ = − 1 ⋅ 8r = −4r
A II = 5r ⋅ 8r = 40r 2 ,
xc 2
yc 2
2
2
2
1
2
~ = 4 ⋅ 2r = 8r ,
~ = − 4 ⋅ 2r = − 8r
A III = ⋅ π ⋅ (2r ) = πr 2 ,
xc 3
yc3
4
3 ⋅ π 3π
3⋅π
3π
1
15
~ = 2r + 2 ⋅ 3r = 4r , ~ = − 1 ⋅ 5r = − 5 r
xc 4
yc 4
A IV = ⋅ 3r ⋅ 5r = r 2 ,
3
2
2
3
3
Całkowite pole figury wynosi:
9 2
15
πr + 40r 2 − πr 2 − r 2 = 43.496r 2
2
2
Moment statyczny względem osi y wynosi:
x
S y = A I ⋅ ~c1 + A II ⋅ ~c 2 − A III ⋅ ~c 3 − A IV ⋅ ~c 4 =
x
x
x
A = A I + A II − A III − A IV =
9 2 ⎛ 4r ⎞
5
8r 15 2
πr ⋅ ⎜ − ⎟ + 40r 2 ⋅ r − πr 2 ⋅
− r ⋅ 4r = 49.333r 3
2
2
3π 2
⎝ π ⎠
Moment statyczny względem osi x wynosi:
y
S x = A I ⋅ ~c1 + A II ⋅ ~c 2 − A III ⋅ ~c 3 − A IV ⋅ ~c 4 =
y
y
y
=
9 2
⎛ 8r ⎞ 15 2 ⎛ 5 ⎞
3
πr ⋅ (− 5r ) + 40r 2 ⋅ (− 4r ) − πr 2 ⋅ ⎜ −
⎟ − r ⋅ ⎜ − r ⎟ = −215.519r
2
3π ⎠ 2
3 ⎠
⎝
⎝
Współrzędne środka ciężkości rozpatrywanej figury wynoszą odpowiednio:
3
3
~ = S x = − 215.519r = −4.9549r .
~ = S y = 49.333r = 1.1342r
yc
oraz
xc
A 43.496r 2
A
43.496r 2
=
y
yc
x
O
C
xc
Wyznaczymy momenty bezwładności i moment dewiacyjny w układzie Oxy.
I
II
III
IV
Ix = Ix + Ix − Ix − Ix =
1
9
1
1
1
4
2
3
4
3
= π ⋅ (3r ) + πr 2 ⋅ (− 5r ) + ⋅ 5r ⋅ (8r ) − π ⋅ (2r ) − ⋅ 3r ⋅ (5r ) = 1204.18r 4
8
2
3
16
12
I
II
III
IV
Iy = Iy + Iy − Iy − Iy =
1
1
1
15
⎡1
4
3
4
3
2⎤
= π ⋅ (3r ) + ⋅ 8r ⋅ (5r ) − π ⋅ (2r ) − ⎢ ⋅ 5r ⋅ (3r ) + r 2 ⋅ (4r ) ⎥ = 238.25r 4
8
3
16
2
⎦
⎣ 36
I
II
III
IV
I xy = I xy + I xy − I xy − I xy =
9
⎛ 1
⎛ 4r ⎞ 1
2
2
4⎞
= 0 + πr 2 ⋅ (− 5r ) ⋅ ⎜ − ⎟ − ⋅ (8r ) ⋅ (5r ) − ⎜ − ⋅ (2r ) ⎟ +
2
⎝ 8
⎠
⎝ π⎠ 4
⎡ 1
15
⎛ 5 ⎞⎤
2
2
− ⎢− ⋅ (5r ) ⋅ (3r ) + r 2 ⋅ (4r ) ⋅ ⎜ − r ⎟⎥ = −254.88r 4
2
⎝ 3 ⎠⎦
⎣ 72
Następnie wyznaczymy momenty bezwładności i moment dewiacyjny w układzie osi
centralnych x c i y c korzystając z przekształconych wzorów Steinera:
2
2
I = I − A ⋅ ~ = 1204.18r 4 − 43.496r 2 ⋅ (− 4.9549r ) = 136.31r 4
y
xc
x
c
2
2
I yc = I y − A ⋅ ~c = 238.25r 4 − 43.496r 2 ⋅ (1.1342r ) = 182.30r 4
x
2
I xc yc = I xy − A ⋅ ~c ⋅ ~c = −254.88r 4 − 43.496r 2 ⋅ 1.1342r ⋅ (− 4.9549r ) = −10.44r 4 .
x y
Momenty bezwładności względem głównych centralnych osi bezwładności osiągają
wartości:
I 1 = I max =
I xc + I y c
2
⎛ I x − I yc
+ ⎜ c
⎜
2
⎝
2
⎞
⎟ + I xc y c 2 =
⎟
⎠
⎛ 136.31r 4 − 182.30r 4
136.31r 4 + 182.30r 4
=
+ ⎜
⎜
2
2
⎝
I 2 = I min =
I xc + I y c
2
⎛ I x − I
... zobacz całą notatkę






Komentarze użytkowników (0)