To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
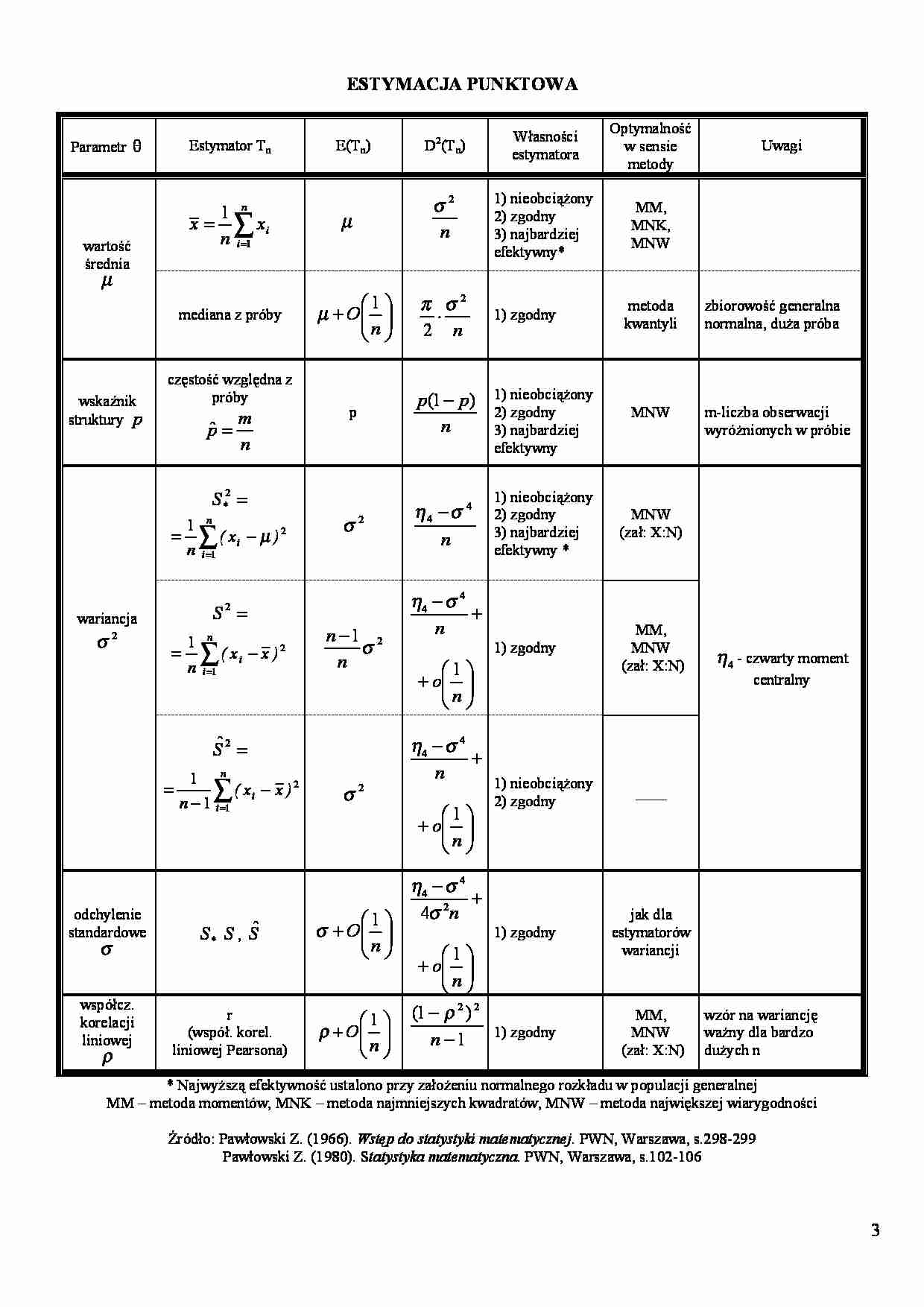

ESTYMACJA PUNKTOWA
Parametr θ
Estymator Tn
1 n
x = ∑ xi
n i =1
wartość
średnia
E(Tn)
µ
µ
mediana z próby
wskaźnik
struktury p
częstość względna z
próby
ˆ
p=
m
n
1
µ + O
n
p
S2 =
wariancja
σ2
1 n
= ∑ ( xi − x ) 2
n i =1
σ2
n −1 2
σ
n
ˆ
S2 =
=
odchylenie
standardowe
σ
współcz.
korelacji
liniowej
ρ
1 n
∑ ( xi − x ) 2
n − 1 i =1
Własności
estymatora
Optymalność
w sensie
metody
σ2
n
1) nieobciążony
2) zgodny
3) najbardziej
efektywny*
MM,
MNK,
MNW
π σ2
⋅
2 n
1) zgodny
p (1 − p ) 1) nieobciążony
2) zgodny
n
3) najbardziej
metoda
kwantyli
MNW
Uwagi
zbiorowość generalna
normalna, duża próba
m-liczba obserwacji
wyróżnionych w próbie
efektywny
S *2 =
1 n
= ∑ ( xi − µ ) 2
n i =1
D2(Tn)
σ2
ˆ
S* S , S
1
σ + O
n
r
(współ. korel.
liniowej Pearsona)
1
ρ + O
n
1) nieobciążony
2) zgodny
3) najbardziej
efektywny *
MNW
(zał: X:N)
1) zgodny
η4 −σ 4
n
MM,
MNW
(zał: X:N)
η4 − σ 4
+
n
1
+ o
n
η4 − σ 4
+
n
1
+ o
n
η4 − σ 4
+
4σ 2 n
1) nieobciążony
2) zgodny
1) zgodny
1
+ o
n
(1 − ρ 2 ) 2
n − 1 1) zgodny
η 4 - czwarty moment
centralny
____
jak dla
estymatorów
wariancji
MM,
MNW
(zał: X:N)
wzór na wariancję
ważny dla bardzo
dużych n
* Najwyższą efektywność ustalono przy założeniu normalnego rozkładu w populacji generalnej
MM – metoda momentów, MNK – metoda najmniejszych kwadratów, MNW – metoda największej wiarygodności
Źródło: Pawłowski Z. (1966). Wstęp do statystyki matematycznej. PWN, Warszawa, s.298-299
Pawłowski Z. (1980). Statystyka matematyczna. PWN, Warszawa, s.102-106
3
Błąd średniokwadratowy estymatora
MSE(Tn)=D2(Tn)+[B(Tn)]2
MSE(Tn)=E(Tn- θ )2 – błąd średniokwadratowy estymatora (ang. Mean Square Error)
MSE( Tn ) jest miarą dokładności estymacji i informuje, o ile przeciętnie wartości estymatora odchylają się
od rzeczywistej wartości parametru.
Czym mniejszy MSE (pierwiastek z MSE) tym większa dokładność.
D2(Tn)= E(Tn- E(Tn))2 – wariancja estymatora ( D( Tn ) = D 2 ( Tn ) - średni błąd szacunku estymatora)
D( Tn ) jest miarą precyzji estymacji i informuje, o ile przeciętnie wartości estymatora odchylają się od
wartości oczekiwanej estymatora.
Czym mniejsza wariancja (średni błąd szacunku) tym większa precyzja.
B(Tn)=E(Tn)- θ - obciążenie estymatora
Gdy obciążenie estymatora wynosi zero to estymator jest nieobciążony czyli oszacowania nie są obciążone
błędem systematycznym. Gdy natomiast obciążenie jest różne od zera to estymator jest obciążony, czyli
oszacowania są obciążone błędem systematycznym.
Uwaga:
Jeśli estymator Tn jest nieobciążony (czyli gdy E(Tn)=Υ) wówczas MSE(Tn)=D2(Tn) i przy interpretacji błędu
szacunku D( Tn ) można skorzystać z interpretacji pierwiastka błędu średniokwadratowego MSE( Tn )
Własności estymatorów
Estymator nazywa się nieobciążonym, jeśli E(Tn)= θ (czyli B(Tn)=0)
Estymator nazywa się asymptotycznie nieobciążonym, jeśli lim B(Tn ) = 0
n →∞
Estymator nazywa się zgodnym, jeśli lim P{Tn − θ
(…)
… normalnego rozkładu w populacji generalnej
MM – metoda momentów, MNK – metoda najmniejszych kwadratów, MNW – metoda największej wiarygodności
Źródło: Pawłowski Z. (1966). Wstęp do statystyki matematycznej. PWN, Warszawa, s.298-299
Pawłowski Z. (1980). Statystyka matematyczna. PWN, Warszawa, s.102-106
3
Błąd średniokwadratowy estymatora
MSE(Tn)=D2(Tn)+[B(Tn)]2
MSE(Tn)=E(Tn- θ )2 – błąd średniokwadratowy…
... zobacz całą notatkę




Komentarze użytkowników (0)