To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
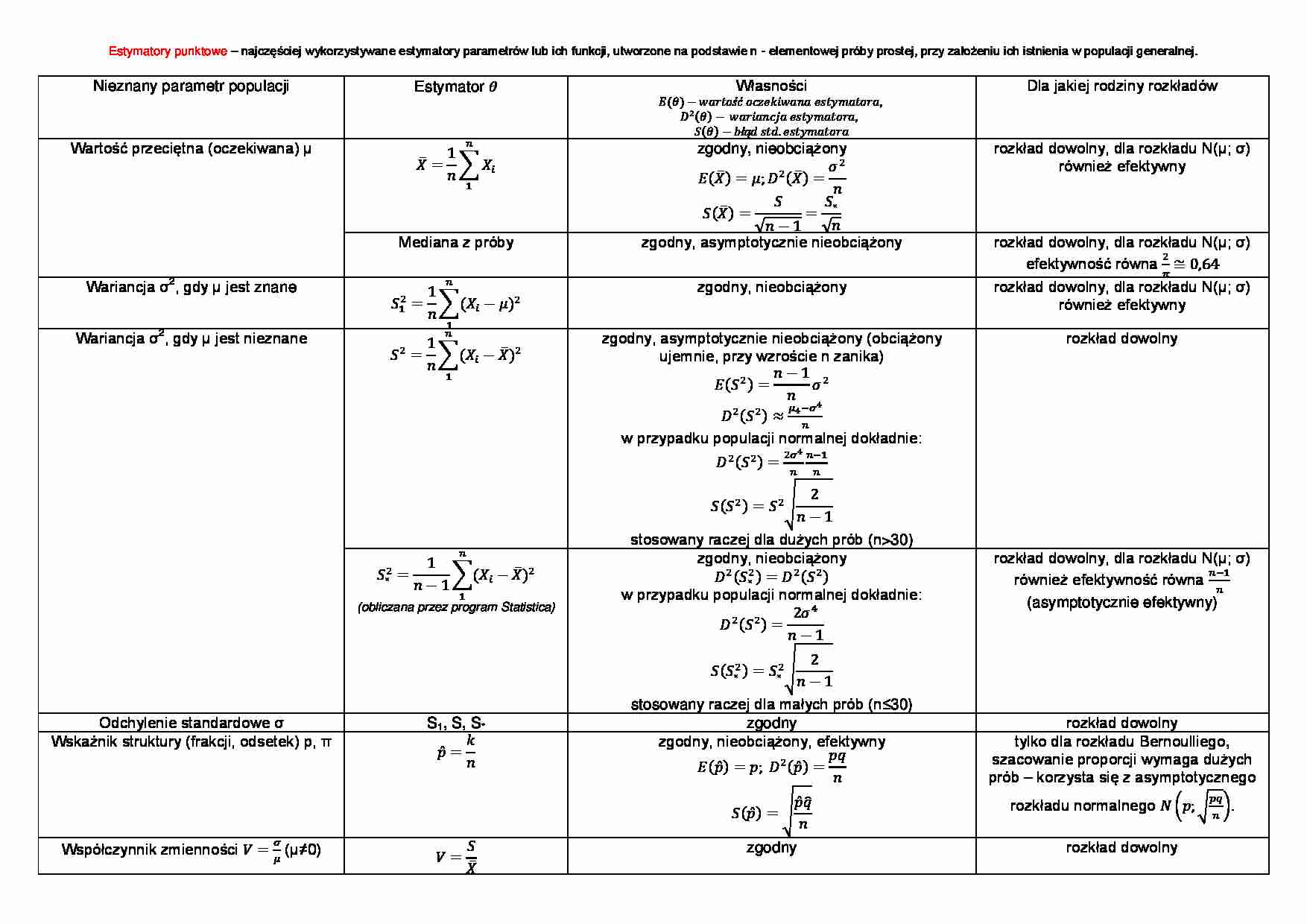


Estymatory punktowe – najczęściej wykorzystywane estymatory parametrów lub ich funkcji, utworzone na podstawie n - elementowej próby prostej, przy założeniu ich istnienia w populacji generalnej. Nieznany parametr populacji Estymator Własności ( ) ( ) ( ) Dla jakiej rodziny rozkładów Wartość przeciętna (oczekiwana) μ ̅ ∑ zgodny, nieobc iążony ( ̅) ( ̅) ( ̅) √ √ rozkład dowolny, dla rozkładu N(μ; σ) również efektywny Mediana z próby zgodny, asymptotycznie nieobciążony rozkład dowolny, dla rozkładu N(μ; σ) efektywność równa Wariancja σ 2, gdy μ jest znane ∑( ) zgodny, nieobciążony rozkład dowolny, dla rozkładu N(μ; σ) również efektywny Wariancja σ 2, gdy μ jest nieznane ∑( ̅) zgodny, asymptotycznie nieobciążony (obciążony ujemnie, przy wzroście n zanika) ( ) ( ) w przypadku populacji normalnej dokładnie: ( ) ( ) √ stosowany raczej dla dużych prób (n30) rozkład dowolny ∑( ̅) (obliczana przez program Statistica) zgodny, nieobciążony ( ) ( ) w przypadku populacji normalnej dokładnie: ( ) ( ) √ stosowany raczej dla małych prób (n≤30) rozkład dowolny, dla rozkładu N(μ; σ) również efektywność równa (asymptotycznie efektywny) Odchylenie standardowe σ S1, S, S* zgodny rozkład dowolny Wskaźnik struktury (frakcji, odsetek) p, π ̂ zgodny, nieobciążony, efektywny ( ̂) ( ̂) ( ̂) √ ̂ ̂ tylko dla rozkładu Bernoulliego, szacowanie proporcji wymaga dużych prób – korzysta się z asymptotycznego rozkładu normalnego ( √ ) Współczynnik zmienności (μ≠0) ̅ zgodny rozkład dowolny Estymacja przedziałowa - określenie przedziału liczbowego, który obejmuje prawdziwą wartość parametru z populacji z góry danym prawdopodobieństwem.
(…)
… N(μ; σ)
również efektywność równa
(asymptotycznie efektywny)
̂̂
rozkład dowolny
tylko dla rozkładu Bernoulliego,
szacowanie proporcji wymaga dużych
prób – korzysta się z asymptotycznego
rozkładu normalnego
( √ )
rozkład dowolny
Estymacja przedziałowa - określenie przedziału liczbowego, który obejmuje prawdziwą wartość parametru z populacji z góry danym prawdopodobieństwem.
Nieznany parametr…
... zobacz całą notatkę






Komentarze użytkowników (0)