To tylko jedna z 7 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

Łączenie rezystorów
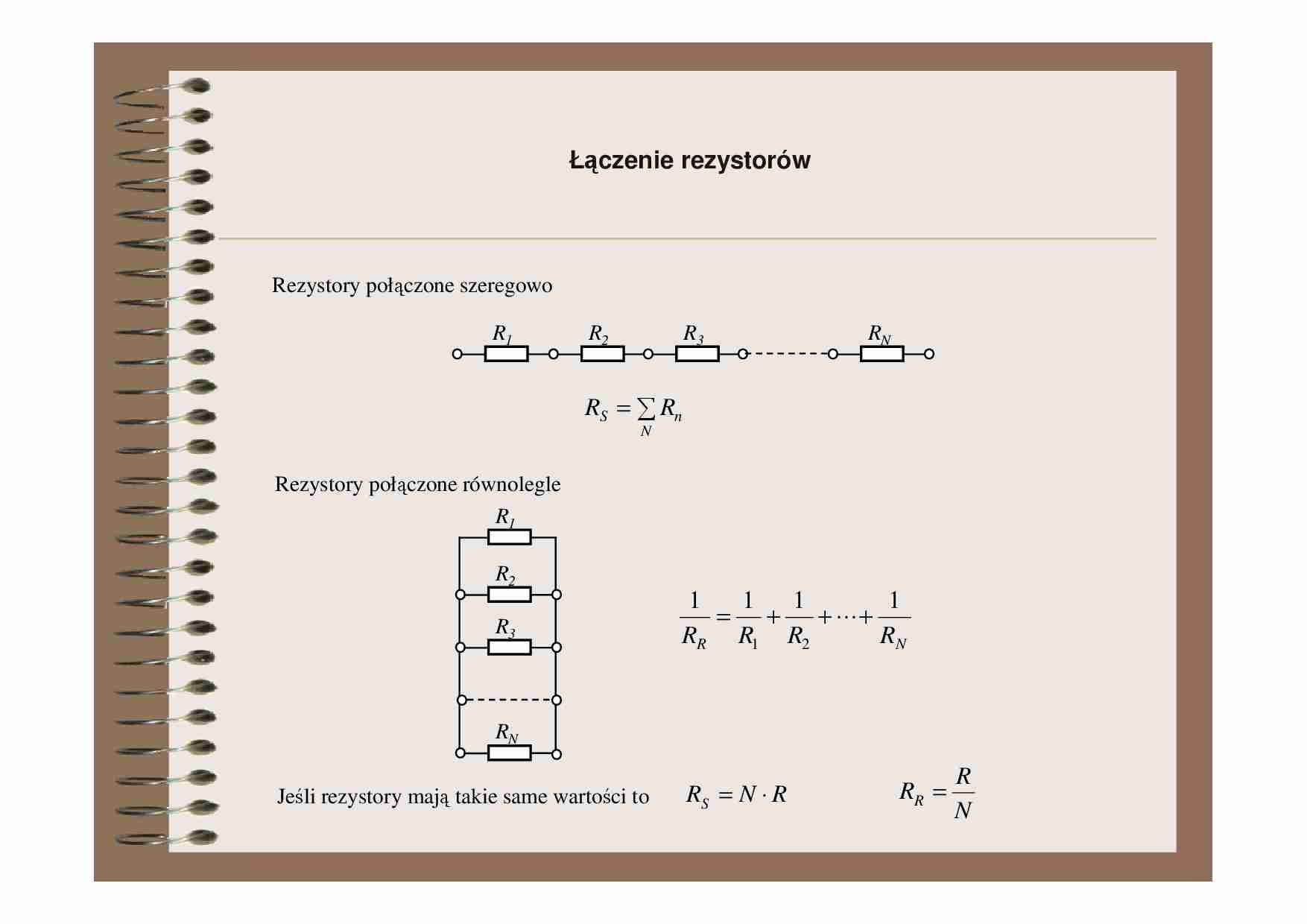
Rezystory połączone szeregowo
R1
R2
R3
RN
RS = ∑ Rn
N
Rezystory połączone równolegle
R1
R2
R3
1
1
1
1
= +
+ ⋅⋅⋅ +
RR R1 R2
RN
RN
Jeśli rezystory mają takie same wartości to
RS = N ⋅ R
RR =
R
N
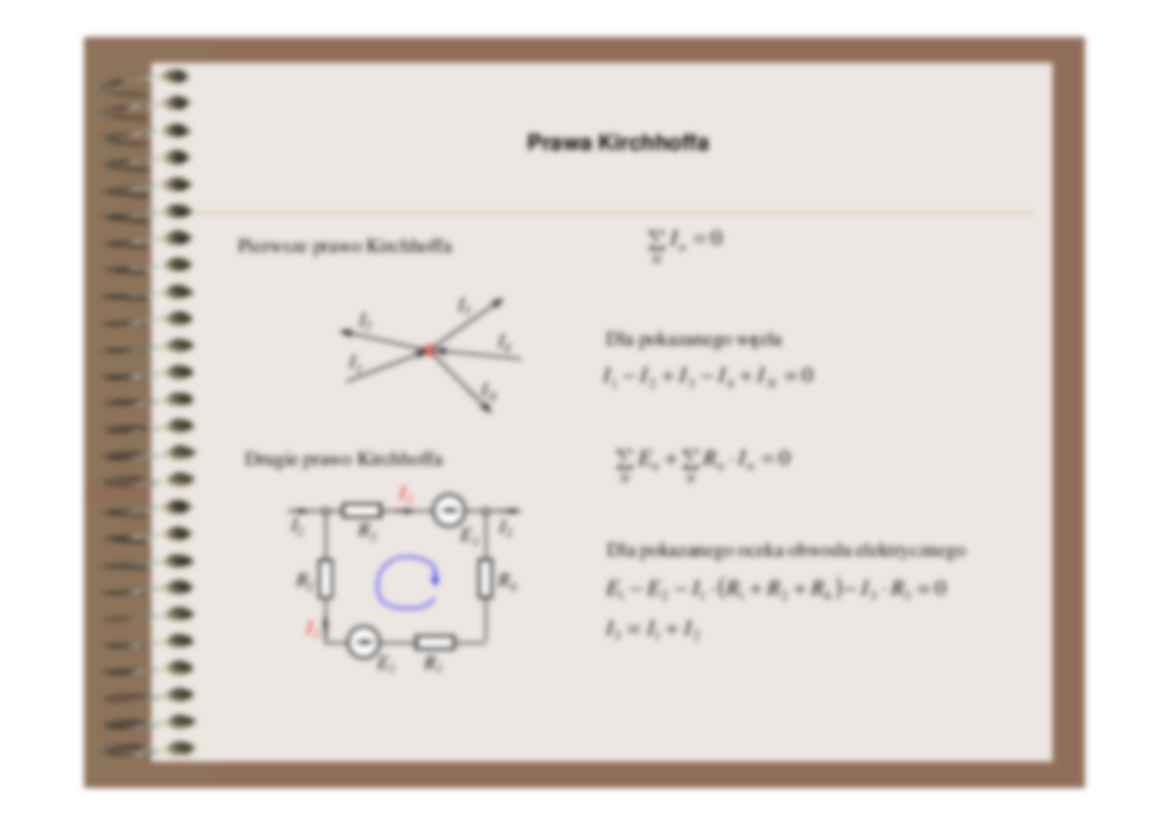
Prawa Kirchhoffa
∑ In = 0
Pierwsze prawo Kirchhoffa
N
I3
I2
I4
I1
I1 − I 2 + I 3 − I 4 + I N = 0
IN
∑ En + ∑ Rn ⋅ I n = 0
Drugie prawo Kirchhoffa
N
I3
I2
Dla pokazanego węzła
R3
E3
R2
N
I2
Dla pokazanego oczka obwodu elektrycznego
R4
E1 − E2 − I1 ⋅ (R1 + R2 + R4 ) − I 3 ⋅ R3 = 0
I 3 = I1 + I 2
I1
E1
R1
Obwody rozgałęzione
2
Liczba gałęzi - 6:
R1
R2
1
3
R5
R4
R3
4
E
R1
R2
R3 R4 R5
Liczba węzłów - 4 (oznaczone cyframi)
Liczba oczek (połączonych ze sobą gałęzi,
tworzących drogę zamkniętą dla prądu) - 3
E
Obwody rozgałęzione
2
R1
Liczba gałęzi - 5:
R2
1
3
R4
R3
R2
R1
R3 R4 − − E
Liczba węzłów - 4 (oznaczone cyframi)
Liczba oczek (połączonych ze sobą gałęzi,
tworzących drogę zamkniętą dla prądu) - 2
R12
4
E
1
R34
Rezystory R1 i R2 oraz R3 i R4 są połączone szeregowo, czyli
R12 = R1 + R2
R34 = R3 + R4
Natomiast rezystory R12 i R34 równolegle, a więc
RZ =
R12 ⋅ R34
R12 + R34
E
RZ
E
3
Przykład obliczeniowy
R6
3
R4
a
R1
d I5
I3
I4
I1
R5
2
1
- węzłów
- gałęzi
- oczek
I6
c
I2
R2
R3
E2
E1
w=4
g=6
o=3
- dla węzła a:
- dla węzła b:
- dla węzła c:
- dla węzła d:
b
- dla oczka 1:
E2 = R2 ⋅ I 2 + R5 ⋅ I 5 + R3 ⋅ I 3
- dla oczka 3:
I1 = I 4 + I 6
I 3 = I1 + I 2
I 2 = I5 − I6
I3 = I 4 + I5
I 3 = I 1 − I 6 + I 2 + I 6 = I1 + I 2
E1 = R1 ⋅ I1 + R4 ⋅ I 4 + R3 ⋅ I 3
- dla oczka 2:
równań
rw = w - 1= 3
równań
ro = g – w + 1 = 3
0 = R6 ⋅ I 6 + R5 ⋅ I 5 − R4 ⋅ I 4
Mając sześć równań moŜemy wyznaczyć sześć wartości prądów,
a następnie spadki napięć czy dokonać bilansu mocy.
Bilans mocy
R6
R4
a
I1
U1
Napięcia na poszczególnych gałęziach:
d I5
I3
I4
U3
U b − c = − E2 + R2 ⋅ I 2
c
I2
U2
R1
U a −b = E1 − U1 = E1 − R1 ⋅ I1
I6
R5
U b − d = −U 3 = − R3 ⋅ I 3
R2
U a − d = R4 ⋅ I 4
R3
U c − d = R5 ⋅ I 5
E2
E1
U a − c = R6 ⋅ I 6
b
Moce w obwodzie:
2
∑ En ⋅ I n = ∑ Rn ⋅ I n
N
N
2
2
2
2
2
E1 ⋅ I1 + E2 ⋅ I 2 = R1 ⋅ I12 + R2 ⋅ I 2 + R3 ⋅ I 3 + R4 ⋅ I 4 + R5 ⋅ I 5 + R6 ⋅ I 6
Jeśli: E1 = 10
R1 = 3
R4 = 2
I1 = 2
E2 = 20
R2 = 4
I4 = 3
R5 = 1
I 2 = −2
R3 = 8
I 5 = −3
R6 = 5
I3 = 0
I 6 = −1
∑ En ⋅ I n = 60
N
2
∑ Rn ⋅ I n = 60
N
Połączenie w gwiazdę oraz w trójkąt
Przekształcenie trójkąta w gwiazdę
a
Przekształcenie gwiazdy w trójkąt
a
Ra
Ra
Rca
Rc
c
Ra =
Rca
Rab
0
Rbc
Rc
Rb
RΥ =
R∆
3
0
Rb
Rbc
c
b
Rab ⋅ Rca
Rab + Rbc + Rca
Rab ⋅ Rbc
Rb =
Rab + Rbc + Rca
Rbc ⋅ Rca
Rc =
Rab + Rbc + Rca
Jeśli: Rab = Rbc = Rca
Rab
Rab = Ra + Rb +
Ra ⋅ Rb
Rc
Rbc = Rb + Rc +
b
Rb ⋅ Rc
Ra
Rca = Rc + Ra +
Ra = Rb = Rc
Rc ⋅ Ra
Rb
R∆ = 3 ⋅ RΥ
... zobacz całą notatkę






Komentarze użytkowników (0)