Pytanie 1. Na czym polega idea metod bootstrapowych. Pytanie 2. Jaka jest ogólna idea testów serii.
Cel testu serii - sprawdzenie losowości, idea polega na sprawdzeniu czy te wartości (a i b) są dobrze przetasowane ale czy nie są nazbyt dobrze. Pytanie 3. Czym się różni seria od odcinka elementarnego? Pytanie 4. Do jakiego typu generatorów zaliczamy generator kwadratowy, wymień jego wady i zalety. Do generatorów programowych. Zalety - Superszybkie (ze względu na rozwój mocy komputerów), Produkują dodatnie liczby całkowite lub bity, Generator daje liczby losowe spełniające praktycznie wszelkie testy losowości. Wady - Po pewnym czasie generowania robi się krótkookresowy (najczęściej liczba generuje samą siebie) - (np. dla m = 2, s = 6), Ponadto przy losowym doborze punktu startu nie można określić długości nieokresowego ciągu
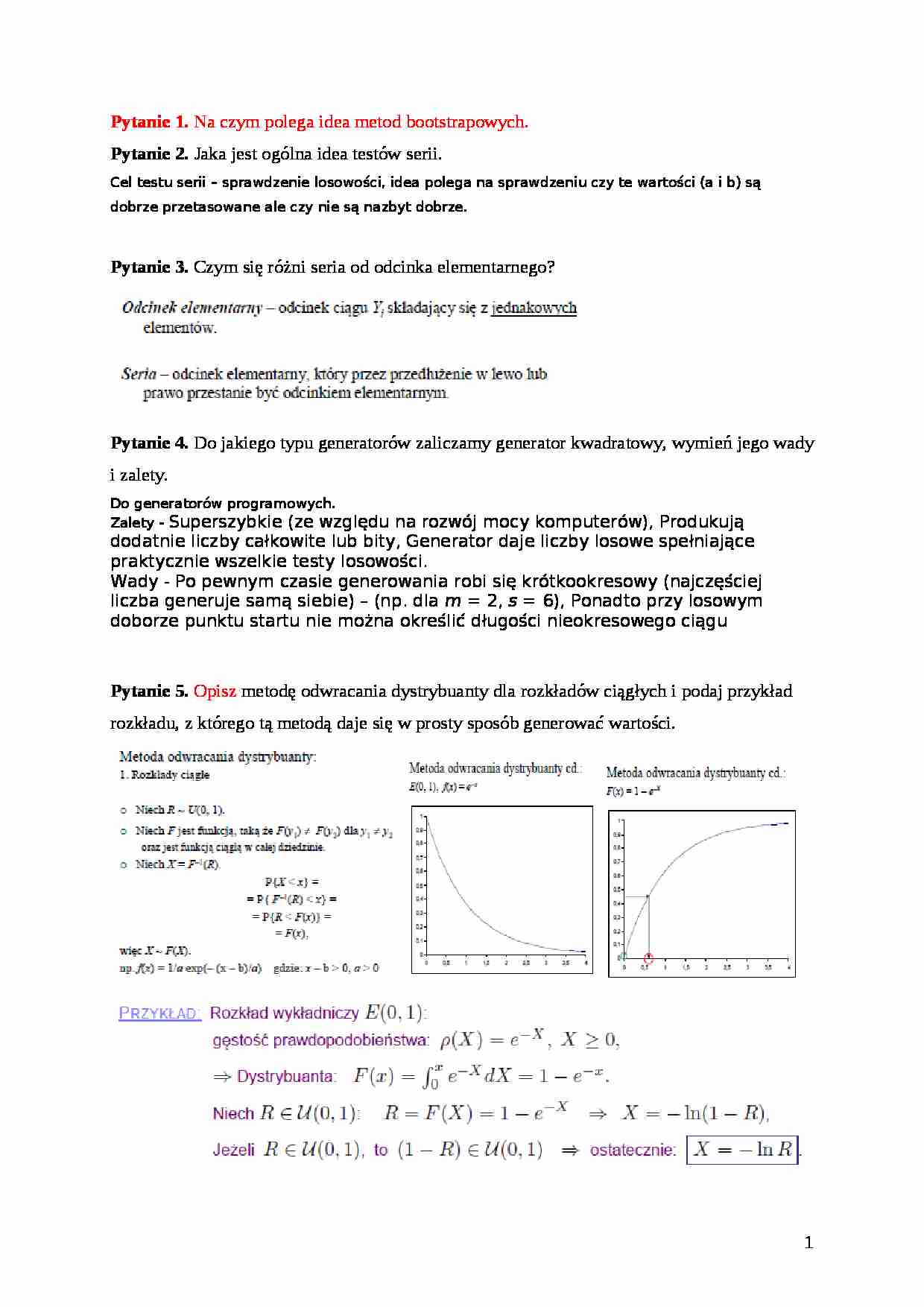
Pytanie 5. Opisz metodę odwracania dystrybuanty dla rozkładów ciągłych i podaj przykład rozkładu, z którego tą metodą daje się w prosty sposób generować wartości.
Pytanie 6. Na czym polega istota testu permutacji?
Test permutacji • Bierzemy cia ֒ g k -wymiarowych punkto´w utworzony z nk kolejnych liczb z generatora: (X1,X2, . . . ,Xk), (Xk+1, . . . ,X2k), . . . , (Xk(n − 1)+1, , . . . ,Xnk) i kaz˙dy z punkto´w przekształcamy zas te ֒ puja ֒ c wspo´ łrze ֒ dne ich rangami (tzn. numerami porza ֒ dkowymi w kolejnos´ci rosna ֒ cej wartos´ci wspo´ łrze ֒ dnych) . ◮ Ka˙zda permutacja (n1, n2, . . . , nk) liczb (1, 2, . . . , k) jest jednakowo prawdopodobna. ⊲ Powyz˙sza ֒ hipoteze ֒ weryfikuje sie ֒ stan dardowym testem chi-kwadrat. Test permutacji • Bierzemy cia ֒ g k -wymiarowych punkto´w utworzony z nk kolejnych liczb z generatora: (X1,X2, . . . ,Xk), (Xk+1, . . . ,X2k), . . . , (Xk(n − 1)+1, , . . . ,Xnk) i kaz˙dy z punkto´w przekształcamy zaste ֒ puja ֒ c wspo ´ łrze ֒ dne ich rangami (tzn. numerami porza ֒ dkowymi w kolejnos´ci rosna ֒ cej wartos´ci wspo´ łrze ֒ dnych) . ◮ Ka˙zda permutacja (n1, n2, . . . , nk) liczb (1, 2, . . . , k) jest jednakowo prawdopodobna. ⊲ Powyz˙sza ֒ hipoteze ֒ weryfikuje sie ֒ standardowym teste m chi-kwadrat. Mając zadany Y1; Y2; : : : rozpatrujemy ciag z o_zony z n grup po t element´ow postaci
(Y1; Y2; : : : ; Yt); (Yt+1; Yt+2; : : : ; Y2t); : : : ; (Y(n¡1)t+1; Y(n¡1)t+2; : : : ; Ynt. Wka_zdej
a n grup jest mo_zliwych t! uporz , adkowa´n element´ow. Nale_zy policzy´c ile razy wyst
, epuje ka_zde uporz , adkowanie, a nast , epnie trzeba zastosowa´c test Â2 dla k = t! oraz
(…)
… 14. Opisz ogólnie istotę poszczególnych rodzajów testów statystycznych stosowanych do oceny generatorów liczb losowych.
4
…
... zobacz całą notatkę





Komentarze użytkowników (0)