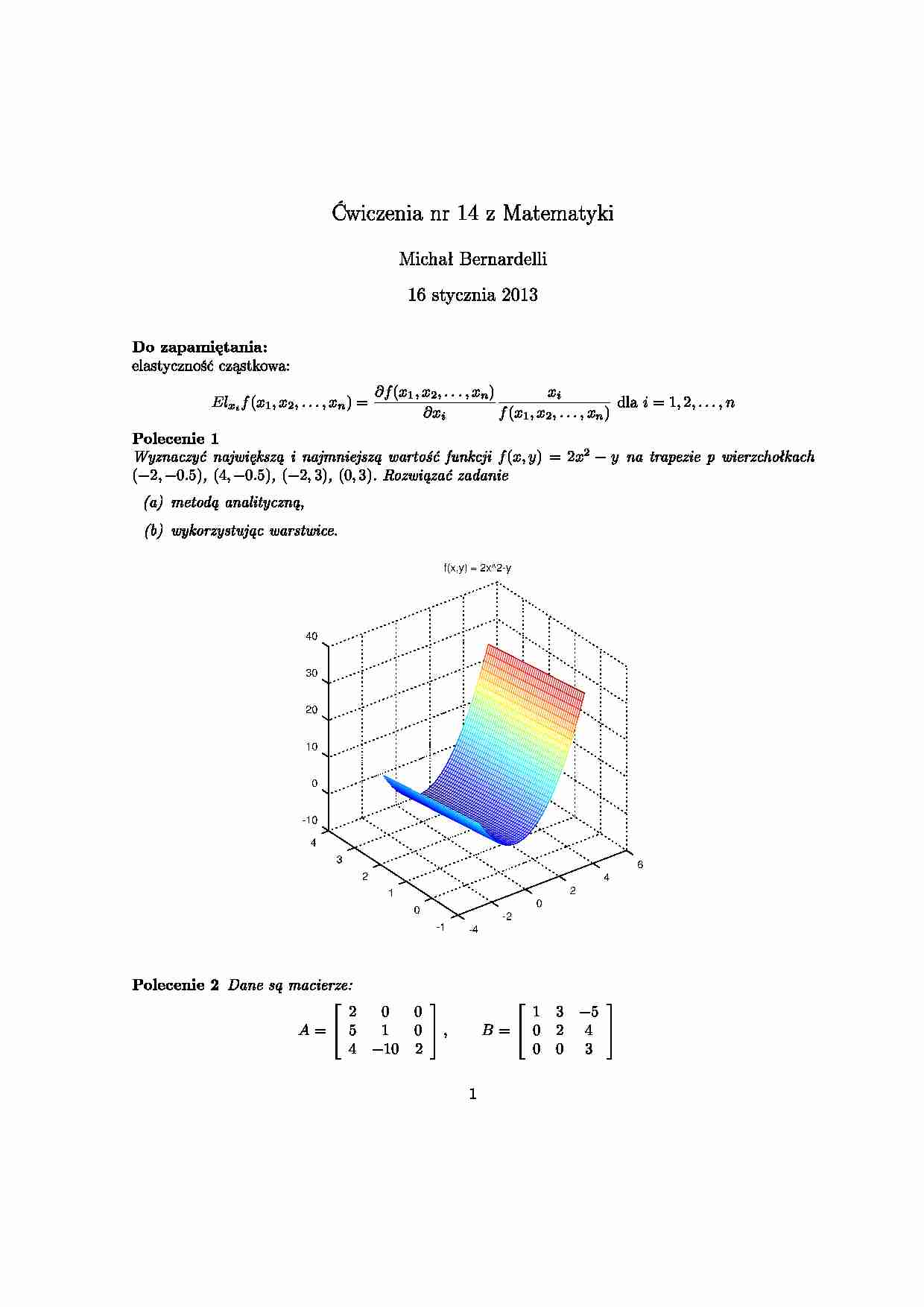
wiczenia nr 14 z Matematyki Michaª Bernardelli 16 stycznia 2013 Do zapami¦tania: elastyczno±¢ cz¡stkowa: Elx i f (x1 , x2 , . . . , xn ) = ∂f (x1, x2, . . . , xn) ∂xi xi f (x1, x2, . . . , xn) dla i = 1, 2, . . . , n Polecenie 1 Wyznaczy¢ najwi¦ksz¡ i najmniejsz¡ warto±¢ funkcji f(x, y) = 2x2 − y na trapezie p wierzchoªkach ( −2, −0.5), (4, −0.5), (−2, 3), (0, 3). Rozwi¡za¢ zadanie (a) metod¡ analityczn¡, (b) wykorzystuj¡c warstwice. Polecenie 2 Dane s¡ macierze: A = 2 0 0 5 1 0 4 −10 2 , B = 1 3 −5 0 2 4 0 0 3 1 oraz macierz C stopnia 3, taka »e det C = 1. Obliczy¢ det(3A) i det ( 3B−1CT A ) . Polecenie 3 Policzy¢ wyznacznik macierzy: 2 1 1 · · · 1 1 1 2 1 · · · 1 1 1 1 2 · · · 1 1 ... ... ... ... ... ... 1 1 1 · · · 2 1 1 1 1 · · · 1 2 . Polecenie 4 Znale¹¢ wszystkie warto±ci A ∈ R, dla których funkcja f (x) = e Ax 2 jest wypukªa w caªej swojej dziedzinie. Polecenie 5 (do domu) Dla funkcji f (x, y) = x 3 − 4x2 + 2xy − y2 • znale¹¢ minima i maksima lokalne, • znale¹¢ najmniejsz¡ i najwi¦ksz¡ warto±¢, • znale¹¢ minima i maksima globalne na obszarze Ω = ⟨−5, 5⟩ × ⟨−1, 1⟩ = {(x, y) ∈ R2 : x ∈ ⟨−5, 5⟩, y ∈ ⟨−1, 1⟩} ZADANIA DO SAMODZIELNEGO ROZWIZANIA: osoby, ze ±redni¡ z kolokwiów z przedziaªu ⟨10, 15) (dopuszczenie do pierwszego terminu egzaminu) termin oddania rozwi¡zanych zada« 20 stycznia, osoby, ze ±redni¡ z kolokwiów poni»ej 10 (dopuszczenie do drugiego terminu egzaminu) termin oddania rozwi¡zanych zada« 27 stycznia. Polecenie 6 Policzy¢ wyznacznik macierzy: 2 −1 −1 0 −2 2 −1 0 −1 0 −1 1 −1 2 0 0 −1 1 −2 1 2 0 1 0 −1 . Polecenie 7 Obliczy¢ granice ci¡gów (a) an = 2012 n +n2012 2012! −n! , 2 (b) bn = ( n 2 −2n n2+2n −4 ) 4n −3 . Polecenie 8 Obszar D = {(x, y) ∈ R2 : x ∈ ⟨0; 6⟩, y ≥ (x − 3)2, y ≤ 9} zostaª podzielony krzyw¡ y = x2 na dwie cz¦±ci F1 i F2. Oblicz stosunek otrzymanych w ten sposób pól. Polecenie 9 Znale¹¢ eksrema lokalne funkcji f (x) = 1 5 x 5 − 5 3 x 3 + 4x. Okre±li¢ punkty, w których funkcja jest wypukªa. Znale¹¢ najmniejsz¡ i najwi¦ksz¡ warto±¢ funkcji na
(…)
…. Znale¹¢ najmniejsz¡ i najwi¦ksz¡ warto±¢ funkcji na
przedziale ⟨−1, 3⟩.
f (x) =
Polecenie 10
Obliczy¢ caªki:
=
2
∫ √
x x2 − 3 dx
√
>
e
∫
x2 ln x dx
1
3
Polecenie 11
Znale¹¢ dziedzin¦ i asymptoty funkcji
f (x) =
ln |x|
.
x−1
Polecenie 12
Dane s¡ cztery punkty z przestrzeni R4 :
1
1
1
3
A = ,
B = ,
0
0
0
−2
0
0
C = ,
1
1
2
−2
D = .
−1
3
Prosta k przechodzi…
... zobacz całą notatkę





Komentarze użytkowników (0)