To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
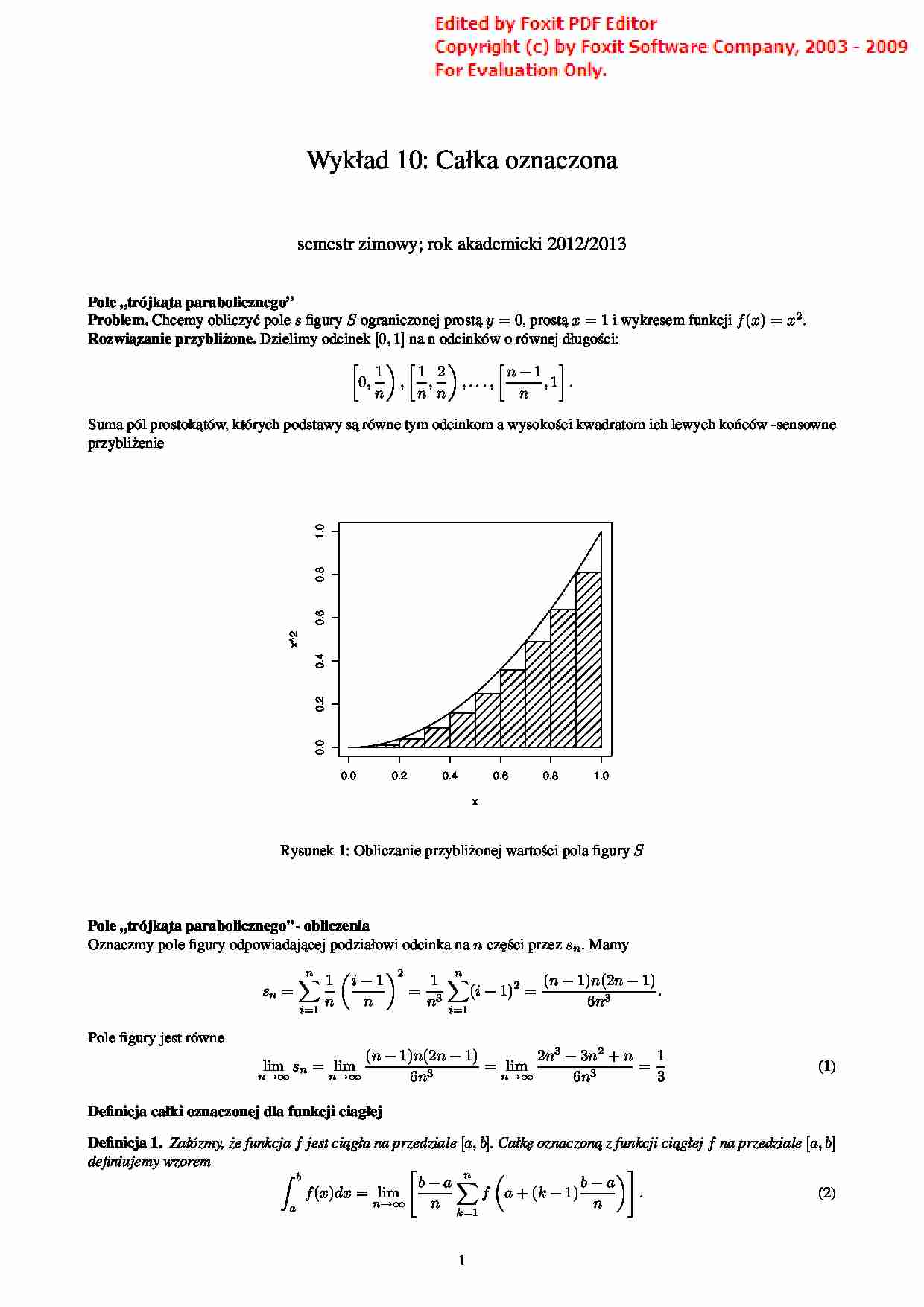


Wykład 10: Całka oznaczona semestr zimowy; rok akademicki 2012/2013 Pole „trójk ˛ ata parabolicznego” Problem. Chcemy obliczy´c pole s figury S ograniczonej prost ˛ a y = 0, prost ˛ a x = 1 i wykresem funkcji f ( x ) = x 2. Rozwi ˛ azanie przybli˙zone. Dzielimy odcinek [0 , 1] na n odcinków o równej długo´sci: 0 , 1 n , 1 n , 2 n , . . . , n − 1 n , 1 . Suma pól prostok ˛ atów, których podstawy s ˛ a równe tym odcinkom a wysoko´sci kwadratom ich lewych ko´nców -sensowne przybli˙zenie 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 x x^2 Rysunek 1: Obliczanie przybli˙zonej warto´sci pola figury S Pole „trójk ˛ ata parabolicznego"- obliczenia Oznaczmy pole figury odpowiadaj ˛ acej podziałowi odcinka na n cz˛e´sci przez sn . Mamy sn = n i =1 1 n i − 1 n 2 = 1 n 3 n i =1 ( i − 1) 2 = ( n − 1) n (2 n − 1) 6 n 3 . Pole figury jest równe lim n→∞ sn = lim n→∞ ( n − 1) n (2 n − 1) 6 n 3 = lim n→∞ 2 n 3 − 3 n 2 + n 6 n 3 = 1 3 (1) Definicja całki oznaczonej dla funkcji ciagłej Definicja 1. Załózmy, ˙ze funkcja f jest ci ˛ agła na przedziale [ a, b ]. Całk˛e oznaczon ˛ a z funkcji ci ˛ agłej f na przedziale [ a, b ] definiujemy wzorem b a f ( x ) dx = lim n→∞ b − a n n k =1 f a + ( k − 1) b − a n . (2) 1 Korzystaj ˛ ac z wprowadzonej notacji, pole „trójk ˛ ata parabolicznego” mo˙zna wyrazi´c nast˛epuj ˛ aco: 1 0 x 2 dx. Definicja całki oznaczonej dla funkcji przedziałami ciagłej Uwaga 1. Wzorem (2) mo˙zna zdefiniowa´c całk˛e oznaczon ˛ a dla pewnych funkcji nieci ˛ agłych, np. dla funkcji przedziałami ci ˛ agłych. Funkcj˛e f nazywamy przedziałami ci ˛ agł ˛ a na przedziale [ a, b ], je˙zeli istniej ˛ a liczby c 1 , c 2 , . . . , ck takie, ˙ze: (i) a
(…)
…], to
z
˛
b
f (x)dx = F (b) − F (a),
a
gdzie F oznacza dowolna funkcj˛ pierwotna funkcji f na tym przedziale.
˛
e
˛
2
(4)
Twierdzenie to ma intepretacj˛ fizyczna: Droga przebyta przez punkt materialny na przedziale czasowym [a, b] jest równa
e
˛
V (b) − V (a), gdzie V jest dowolna funkcja pierwotna pr˛ dko´ci v na [a, b]. Precyzyjny dowód Tw. Newtona-Leibniza
˛
˛
˛ e s
˙
mozna znale´ c np. ksiazce W. Rudina…
… odpowiadajacego funkcji f (x) = x i odcinkowi [1, b].
z´
˛
Pole to jest równe:
b
1
dx = [ln x]b = ln b − ln 1 = ln b.
1
1 x
Zastosowania całki oznaczonej— obliczanie pola figur— c.d.
y
y =
0
1
x
x
b
1
Rysunek 3: Logarytm naturalny liczby b > 1 jako pole trapezu krzywoliniowego odpowiadajacemu funkcji f (x) =
˛
odcinkowi [1, b].
1
x
i
Zastosowania całki oznaczonej— droga przebyta przez punkt materialny
˙
Punkt…
… f (x) pomnozonemu przez (-1).
Zastosowanie do obliczania drogi przebytej w ruchu zmiennym
˙ ˛
Punkt materialny porusza si˛ ruchem prostoliniowym z pr˛ dko´cia v(t) zalezna od czasu. Chcemy znale´ c drog˛ s przee
e s ˛
z´
e
˙
byta przez ten punkt w przedziale czasowym [a, b]. Zakładamy, ze funkcja v jest ciagła.
˛
˛
Podzielmy przedział [a, b] na n odcinków o równej długo´ci:
s
[t0 , t1 ), [t1 , t2…
... zobacz całą notatkę






Komentarze użytkowników (0)