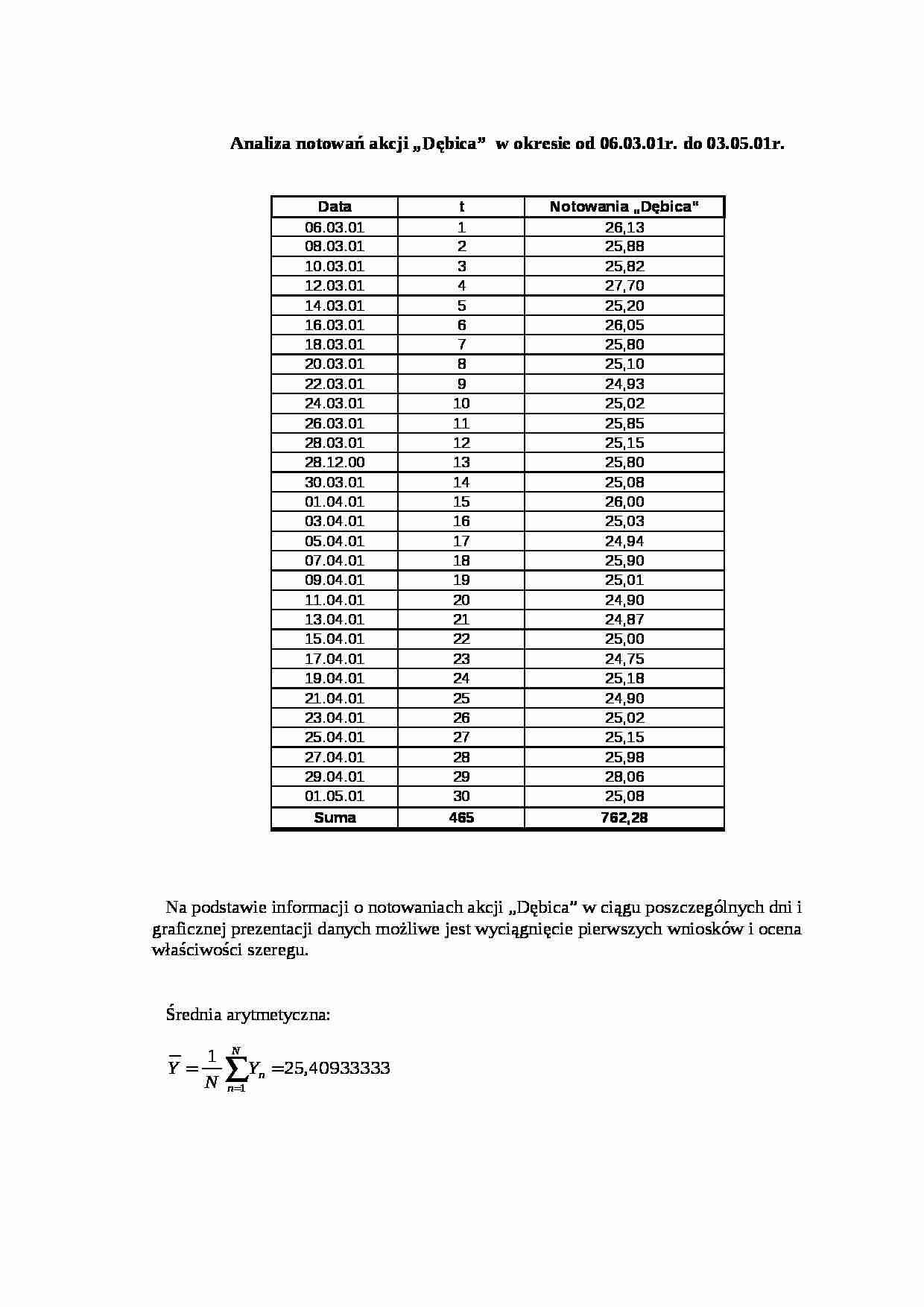
Analiza notowań akcji „Dębica” w okresie od 06.03.01r. do 03.05.01r.
Data
t
Notowania „Dębica“
06.03.01
1
26,13
08.03.01
2
25,88
10.03.01
3
25,82
12.03.01
4
27,70
14.03.01
5
25,20
16.03.01
6
26,05
18.03.01
7
25,80
20.03.01
8
25,10
22.03.01
9
24,93
24.03.01
10
25,02
26.03.01
11
25,85
28.03.01
12
25,15
28.12.00
13
25,80
30.03.01
14
25,08
01.04.01
15
26,00
03.04.01
16
25,03
05.04.01
17
24,94
07.04.01
18
25,90
09.04.01
19
25,01
11.04.01
20
24,90
13.04.01
21
24,87
15.04.01
22
25,00
17.04.01
23
24,75
19.04.01
24
25,18
21.04.01
25
24,90
23.04.01
26
25,02
25.04.01
27
25,15
27.04.01
28
25,98
29.04.01
29
28,06
01.05.01
30
25,08
Suma
465
762,28
Na podstawie informacji o notowaniach akcji „Dębica” w ciągu poszczególnych dni i graficznej prezentacji danych możliwe jest wyciągnięcie pierwszych wniosków i ocena właściwości szeregu.
Średnia arytmetyczna:
Bazując na drugim wykresie można łatwo zauważyć, jak przebiega przybliżona linia trendu. Jest ona opadająca w ciągu całego badanego okresu, co oznacza, że kurs EURO spada.
Szukamy linii trendu:
gdzie
Kryterium weryfikacji modelu
Aby wyznaczyć parametry prostej, dla której suma kwadratów reszt jest najmniejsza, korzystamy z warunków koniecznych istnienia ekstremum.
(…)
… należy zbadać przy pomocy funkcji autokorelacji.
Identyfikacja modelu AR.
Zakładamy, że obserwowany proces będzie opisany modelem autoregresji rzędu II.
AR(2)
Kryterium identyfikacji modelu
Warunek konieczny istnienia ekstremum
Warunek istnienia rozwiązania:
Obliczenie wartości parametrów a1 i a2 z wyznaczników:
W = 12022874,7
Model autoregresji rzędu II dopasowany do analizowanych danych, a więc obrazujący wahania notowań akcji „Dębica”, ma postać:
Należy zbadać wzajemną korelację pomiędzy wyrazami reszt. Do tego celu służy funkcja autokorelacji.
Funkcja autokorelacji wyraża się wzorem:
Nie unormowana funkcja autokorelacji jest kowariancją (estymatorem kowariancji) procesu Et. Wyraża się wzorem:
Funkcja autokorelacji w zerze:
Wyliczono 7 kroków funkcji autokorelacji:
K(0)= 0,3833099 K(1)= 0,0516081…
... zobacz całą notatkę





Komentarze użytkowników (0)