To tylko jedna z 10 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
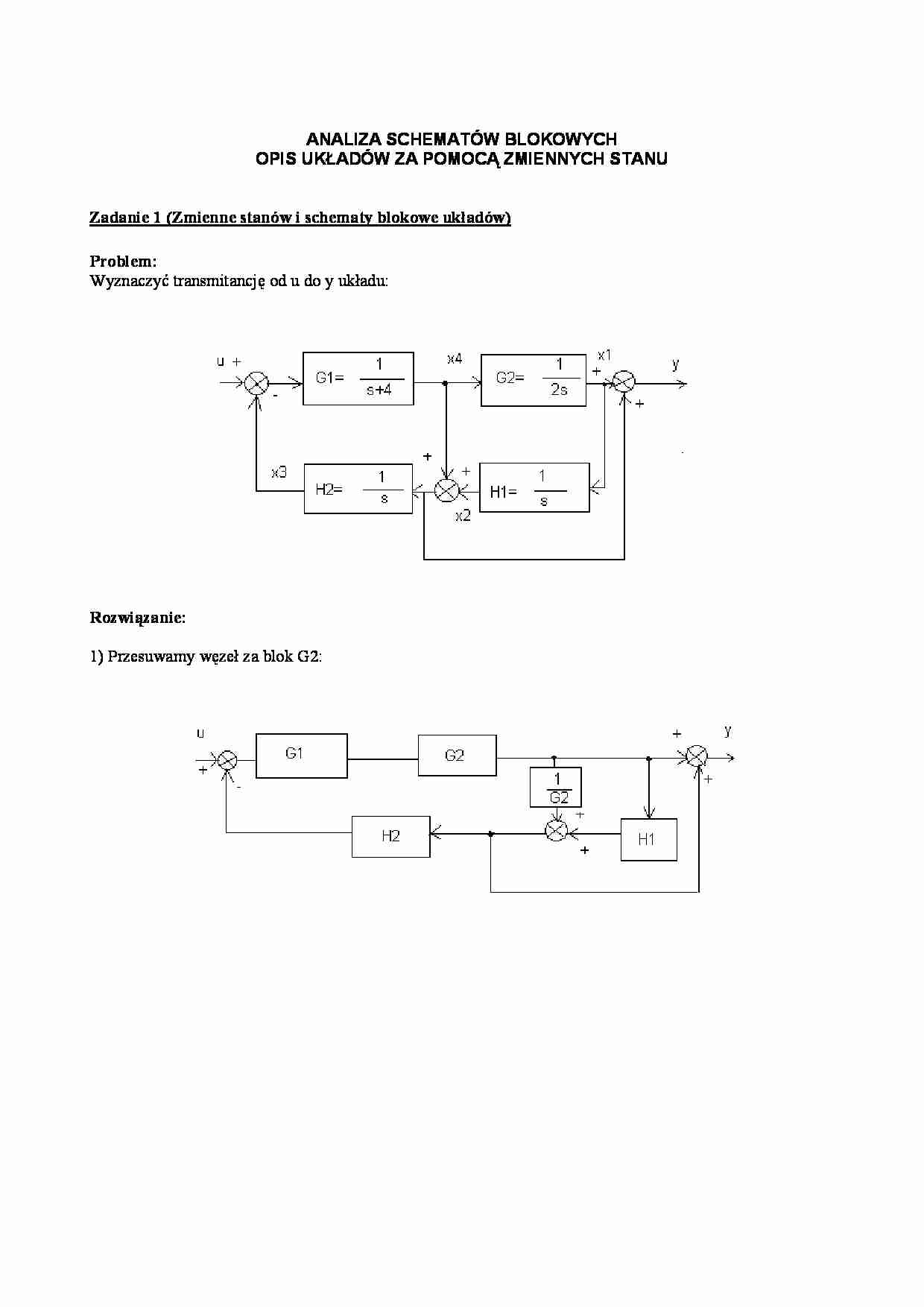

ANALIZA SCHEMATÓW BLOKOWYCH
OPIS UKŁADÓW ZA POMOCĄ ZMIENNYCH STANU
Zadanie 1 (Zmienne stanów i schematy blokowe układów)
Problem:
Wyznaczyć transmitancję od u do y układu:
Rozwiązanie:
1) Przesuwamy węzeł za blok G2:
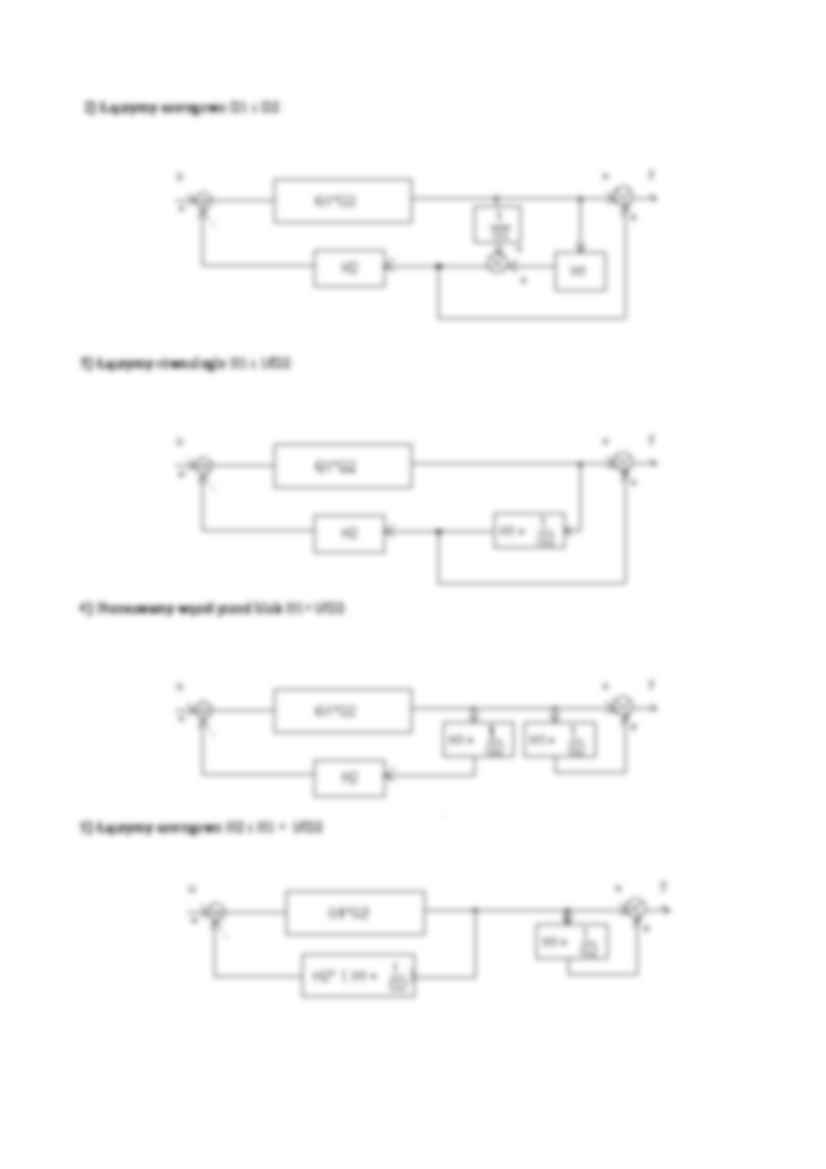
2) Łączymy szeregowo G1 i G2 :
3) Łączymy równolegle H1 i 1/G2:
4) Przesuwamy węzeł przed blok H1+1/G2:
5) Łączymy szeregowo H2 i H1 + 1/G2:
6) Upraszczamy połączenie równoległe po prawej stronie:
7) Upraszczamy sprzężenie zwrotne:
8) Łączymy szeregowo pozostałe dwa układy:
Po podstawieniu poszczególnych transmitancji do wzoru otrzymamy transmitancje wypadkową:
G ( s) =
2s 2 + s + 1
2s 4 + 3s 3 + 2 s 2 + 1
Zadanie 2 (Zmienne stanów i schematy blokowe układów)
Problem:
Napisać równanie stanu i równania wyjścia dla zmiennych stanu z rysunku:
Rozwiązanie:
1
⋅ x4
x1 = G2 ⋅ x4 =
2s
x = H ⋅ x = 1 ⋅ x
1
1
1
2
s
x = H ⋅ ( x + x ) = 1 ⋅ ( x + x )
2
2
4
2
4
3
s
1
x4 = G1 ⋅ (u − x3 ) =
⋅ (u − x3 )
s+4
1
s ⋅ x1 = 2 ⋅ x 4
s ⋅ x = x
2
1
s ⋅ x3 = x 2 + x 4
s ⋅ x 4 + 4 ⋅ x 4 = u − x3 ⇒ s ⋅ x 4 = − x3 − 4 ⋅ x 4 + u
1
⋅ x 4 (t )
2
x 2 (t ) = x1 (t )
(1)
(2)
x1 (t ) =
x3 (t ) = x 2 (t ) + x 4 (t )
x 4 (t ) = − x3 (t ) − 4 ⋅ x 4 (t ) + u (t )
(3)
Równanie stanu:
&
x1
x
&
2 =
x3
&
&
x4
1 x
0 0 0
1
2 x
1 0 0
0 * 2 +
1 x3
0 1 0
0 0 − 1 − 4 x4
1442443
4
4
A
0
0
*u
0
1
{
(4)
B
Równanie wyjścia:
y = C ⋅ x + D ⋅ u = x1 + x 2 + x 4
(5)
x1
x
y = [1 1 0 1] ⋅ 2
x3
x4
(6)
Przykłady przekształcania transmitancji na zmienne stanu
Metoda bezpośrednia
Przykład 1
G ( s) =
s
s +1
1
s s
1
Y ( s)
⋅ =
=
1 U ( s)
s +1 1
1+
s
s
U ( s) Y ( s)
=
= E ( s)
1
1
1+
s
Y (s) = E (s)
U ( s)
= E ( s)
1
1+
s
1
1
U ( s ) = E ( s ) ⋅ 1 + = E ( s ) + ⋅ E ( s )
s
s
1
E ( s) = U ( s) − ⋅ E ( s)
s
Równanie zmiennych stanu
•
x = − x1 + u
•
x = [− 1]⋅ [x1 ] + [1]⋅ [u ]
•
y = x = − x1 + u
[ y ] = [− 1]⋅ [x1 ] + [1]⋅ [u ]
Mnożąc licznik i mianownik transmitancji przez s-n
otrzymamy
G ( s) =
bn −1 s −1 + ... + b1 s 1− n + b0 s − n
Y (s)
prz
=
U ( s ) 1 + a n −1 s −1 + ... + a1 s 1− n + a0 s − n
y czym Y(s) i U(s) są odpowiednio transformatą
Laplace’a odpowiedzi i wymuszenia.
W zależności mamy:
Y ( s ) = (bn −1 s −1 + ... + b1 s 1−n + b0 s − n ) E ( s )
przy czym
E ( s) =
U ( s)
1 + a n −1 s + ... + a1 s 1− n + a0 s − n
−1
Zależność możemy również zapisać w postaci:
E ( s ) = U ( s ) − (a n −1 s −1 + ... + a1 s 1− n + a 0 s − n ) E ( s )
Y(s)
E(s) s-1
E(s)
U(s)
∫
x1
•
x
-1
Przykład 2
G (s) =
Równanie zmiennych stanu –
W następnych przykładach nie
będzie one wyprowadzone.
Y ( s)
2s + 3
=
s + s + 1 U ( s)
2
Y ( s)
2s + 3 s −2
2s −1 + 3s − 2
⋅ −2 =
=
2
−1
−2
U ( s)
s + s +1 s
1+ s + s
U ( s)
Y (s)
= −1
= E (s)
−1
−2
1+ s + s
2 s + 3s −2
Y ( s)
= E ( s)
−1
2s + 3s − 2
Y ( s ) = E ( s ) ⋅ 2s −1 + 3s − 2 = 2 ⋅ E ( s ) ⋅ s −1 + 3E ⋅ ( s ) ⋅ s − 2
U ( s)
= E ( s ) ⇒ U ( s ) = E ( s )
... zobacz całą notatkę






Komentarze użytkowników (0)