Analiza całek oznaczonych - ćwiczenia

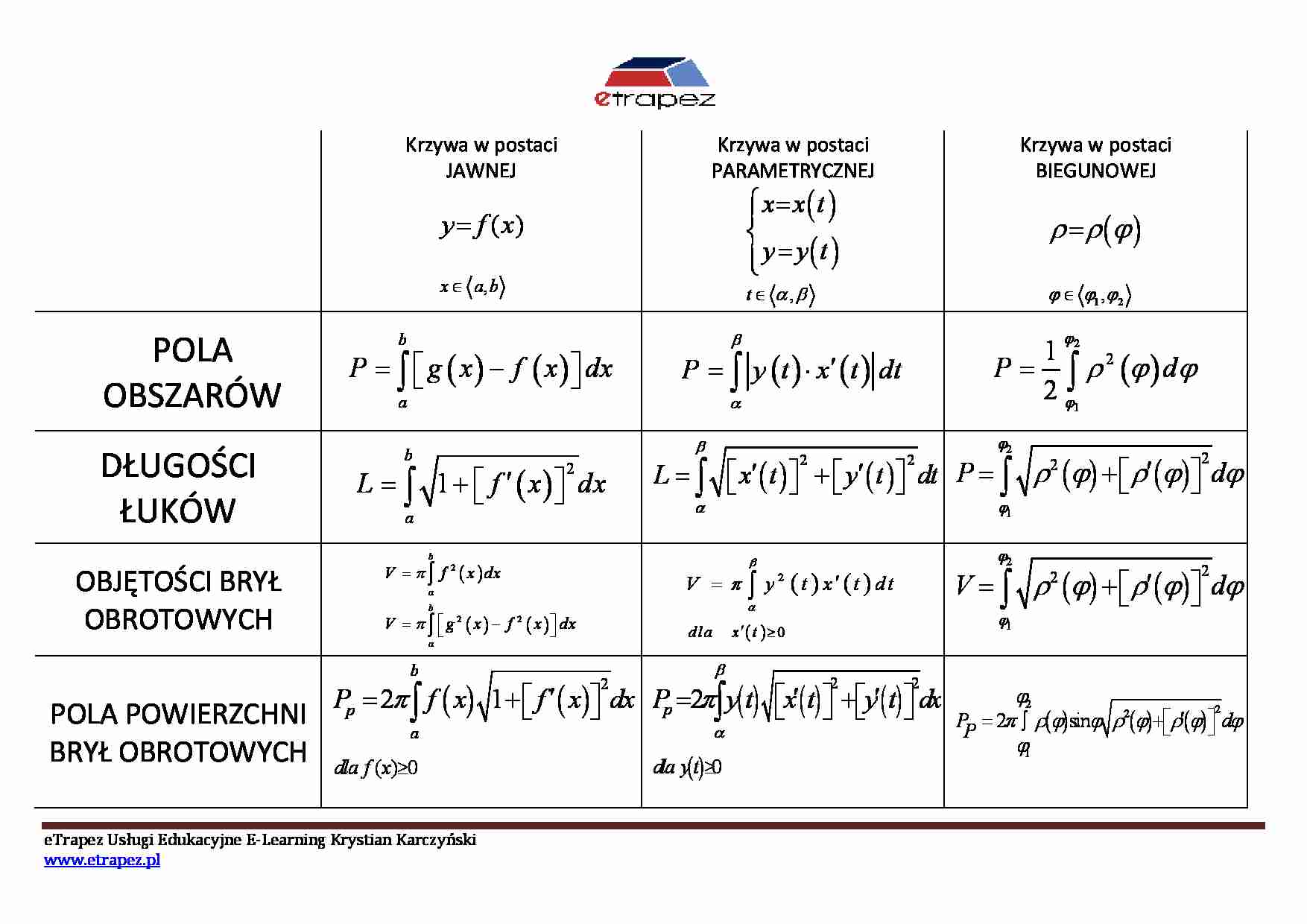
Krzywa w postaci
JAWNEJ
Krzywa w postaci
PARAMETRYCZNEJ
 x = x( t )


 y = y( t )

y = f ( x)
x ∈ a, b
POLA
OBSZARÓW
DŁUGOŚCI
ŁUKÓW
P = ∫  g ( x ) − f ( x )  dx


a
L = ∫ 1 +  f ′ ( x )  dx


2
a
OBJĘTOŚCI BRYŁ
OBROTOWYCH
2
α
b
2
∫
y
2
ϕ2
V = ∫ ρ 2 (ϕ ) + ρ′ (ϕ )  dϕ


(t ) x ′ (t ) d t
β
p
′  ′ 
 ′ 
POLA POWIERZCHNI Pp = 2π ∫ f ( x) 1+ f ( x) dx P =2π∫ y( t) x ( t)  +y ( t) dx
BRYŁ OBROTOWYCH
a
α
dla f ( x)≥0
dla y( t)≥0
eTrapez Usługi Edukacyjne E-Learning Krystian Karczyński
www.etrapez.pl
2
ϕ1
x ′ ( t )≥ 0
d la
2
2
ϕ1
α
a
b
2
α
( x ) dx

ϕ2
L = ∫  x′ ( t )  +  y′ ( t )  dt P = ∫ ρ 2 (ϕ ) + ρ′ (ϕ )  dϕ



 

2
V =π
a
ϕ
1 2 2
P = ∫ ρ (ϕ ) d ϕ
2 ϕ1
P = ∫ y ( t ) ⋅ x′ ( t ) dt
β
( x ) dx
V = π ∫ g2 (x) − f

ϕ ∈ ϕ1 , ϕ2
β
β
b
b
ρ = ρ (ϕ )
t ∈ α, β
b
V =π∫ f
Krzywa w postaci
BIEGUNOWEJ
2
2
ϕ2
2
P = 2π ∫ ρ(ϕ) sinϕ ρ2(ϕ)+ρ′(ϕ) dϕ


P
ϕ1
... zobacz całą notatkę