To tylko jedna z 9 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
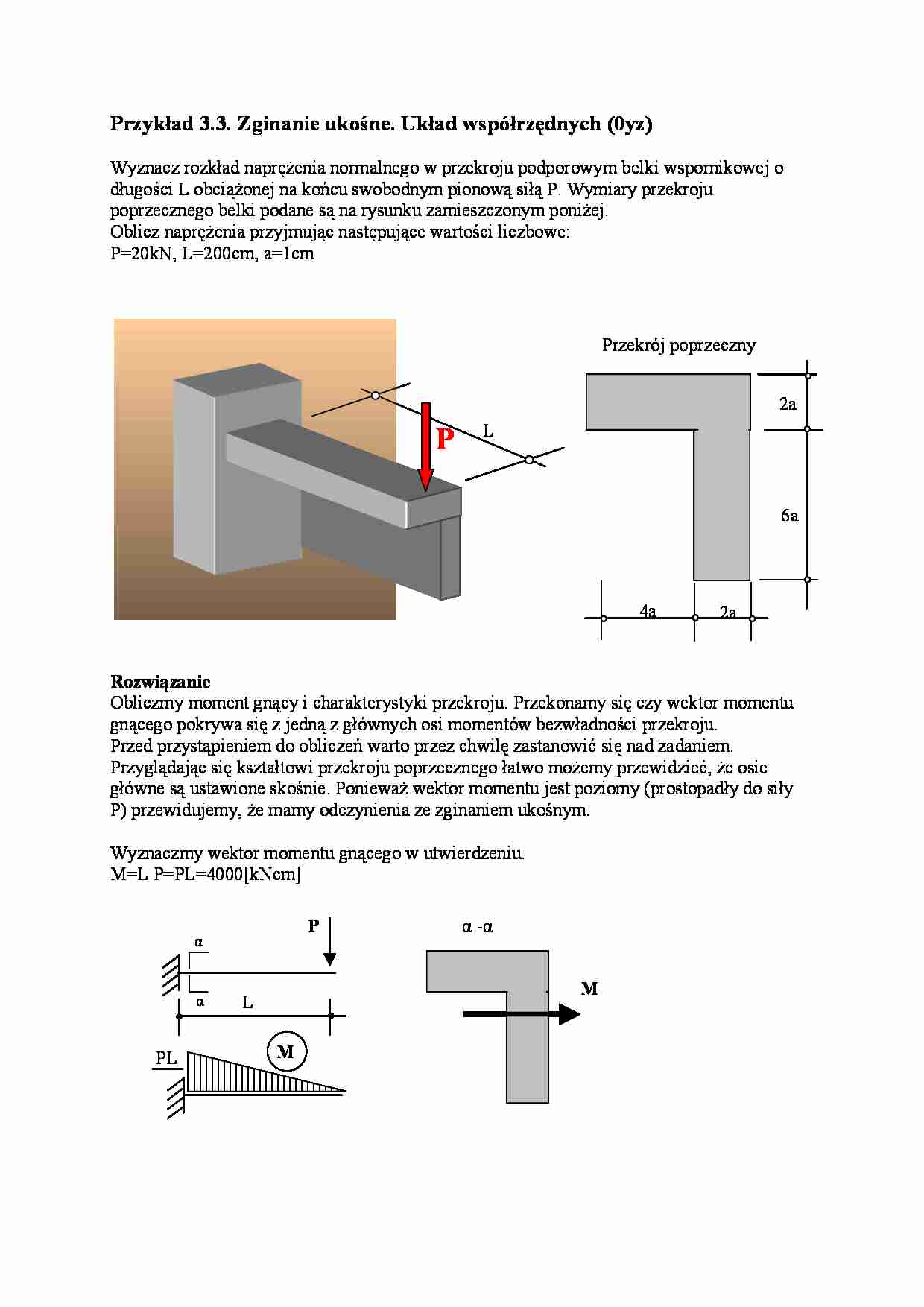


Przykład 3.3. Zginanie ukośne. Układ współrzędnych (0yz)
Wyznacz rozkład naprężenia normalnego w przekroju podporowym belki wspornikowej o
długości L obciążonej na końcu swobodnym pionową siłą P. Wymiary przekroju
poprzecznego belki podane są na rysunku zamieszczonym poniżej.
Oblicz naprężenia przyjmując następujące wartości liczbowe:
P=20kN, L=200cm, a=1cm
Przekrój poprzeczny
2a
P
L
6a
4a
2a
Rozwiązanie
Obliczmy moment gnący i charakterystyki przekroju. Przekonamy się czy wektor momentu
gnącego pokrywa się z jedną z głównych osi momentów bezwładności przekroju.
Przed przystąpieniem do obliczeń warto przez chwilę zastanowić się nad zadaniem.
Przyglądając się kształtowi przekroju poprzecznego łatwo możemy przewidzieć, że osie
główne są ustawione skośnie. Ponieważ wektor momentu jest poziomy (prostopadły do siły
P) przewidujemy, że mamy odczynienia ze zginaniem ukośnym.
Wyznaczmy wektor momentu gnącego w utwierdzeniu.
M=L P=PL=4000[kNcm]
P
α
α
PL
α -α
M
L
M
Obliczmy momenty bezwładności przekroju poprzecznego.
Podzielimy figurę na dwa prostokąty, wyznaczymy środek ciężkości i wartość momentów
bezwładności względem osi centralnych.
I
2a
Współrzędne środka ciężkości
wyznaczamy ze wzorów:
zc =
6a
II
y
4a
2a
Σ S yi
i
Σ Fi
,
i
yc =
Σ S zi
i
Σ Fi
.
i
z
Fi -oznacza pole powierzchni i-tej figury, na które podzielono cały przekrój.
S yi = Fi z i - jest momentem statycznym względem osi y i-tej figury, na które
podzielono cały przekrój. Moment statyczny względem osi y równy jest iloczynowi
pola powierzchni tej figury przez współrzędną zi jej środka ciężkości.
S zi = Fi y i - jest momentem statycznym względem osi z i-tej figury, na które
podzielono cały przekrój. Moment statyczny względem osi z równy jest iloczynowi
pola powierzchni tej figury przez współrzędną yi jej środka ciężkości.
Rachunki możemy szybko przeprowadzić wykorzystując arkusz kalkulacyjny.
Sz
Sy
F
y
moment
z
moment
nr figury
pole
statyczny
statyczny
powierzchni
I
12 [a2] 3 [a]
36 [a3] -7 [a]
-84 [a3]
II
12 [a2] 5 [a]
60 [a3] -3 [a]
-36 [a3]
24 [a2] 4 [a]
96 [a3] -5 [a] -120 [a3]
zc =
Σ S yi
i
Σ Fi
i
=
96a 3
= 4a
24a 2
yc =
Σ S zi
i
Σ Fi
i
=
− 120a 3
= −5a
24a 2
2
Obliczmy teraz korzystając ze wzorów Steinera wartości momentów bezwładności względem
osi centralnych y i z .Niech osie y1 i z1 oznaczają osie centralne dla poszczególnych figur, na
które podzielono cały przekrój.
I
2a
z1
y1
1a
z
II y1
z1 5a
y
4a
2a
Iz =
6a ⋅ ( 2 a ) 3
2a ⋅ (6a ) 3
+ (2a ) 2 ⋅ 12a +
+ (2a ) 2 ⋅ 12a = 136a 4
12
12
Iy =
2 a ⋅ ( 6a ) 3
6a ⋅ ( 2 a ) 3
+ ( − a ) 2 ⋅ 12a +
+ a 2 ⋅ 12a = 64a 4
12
12
I yz = 0 + (−2a) ⋅ (− a ) ⋅ 12a + 0 + 2a ⋅ a ⋅ 12a = 48a 4
Dalszą część zadania możemy rozwiązać na dwa sposoby.
Można wyznaczyć osie główne centralne, znaleźć współrzędne wektora momentu
gnącego w osiach głównych centralnych i wykorzystać wzór na naprężenia przy zginaniu dla
osi głównych centralnych.
Drugi sposób polega na wykorzystaniu wzoru na naprężenia przy zginaniu
(…)
… przy zginaniu dla
osi głównych centralnych.
Drugi sposób polega na wykorzystaniu wzoru na naprężenia przy zginaniu
wyprowadzonego dla osi centralnych.
Metoda druga jest krótsza, ale daje mniej możliwości sprawdzenia poprawności naszego
rozwiązania.
Rozwiązując metodą pierwszą znamy ustawienie osi głównych i możemy sprawdzić
czy wyznaczona przez nas oś obojętna dla zginania ukośnego jest odchylona od kierunku…
... zobacz całą notatkę






Komentarze użytkowników (0)