To tylko jedna z 9 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


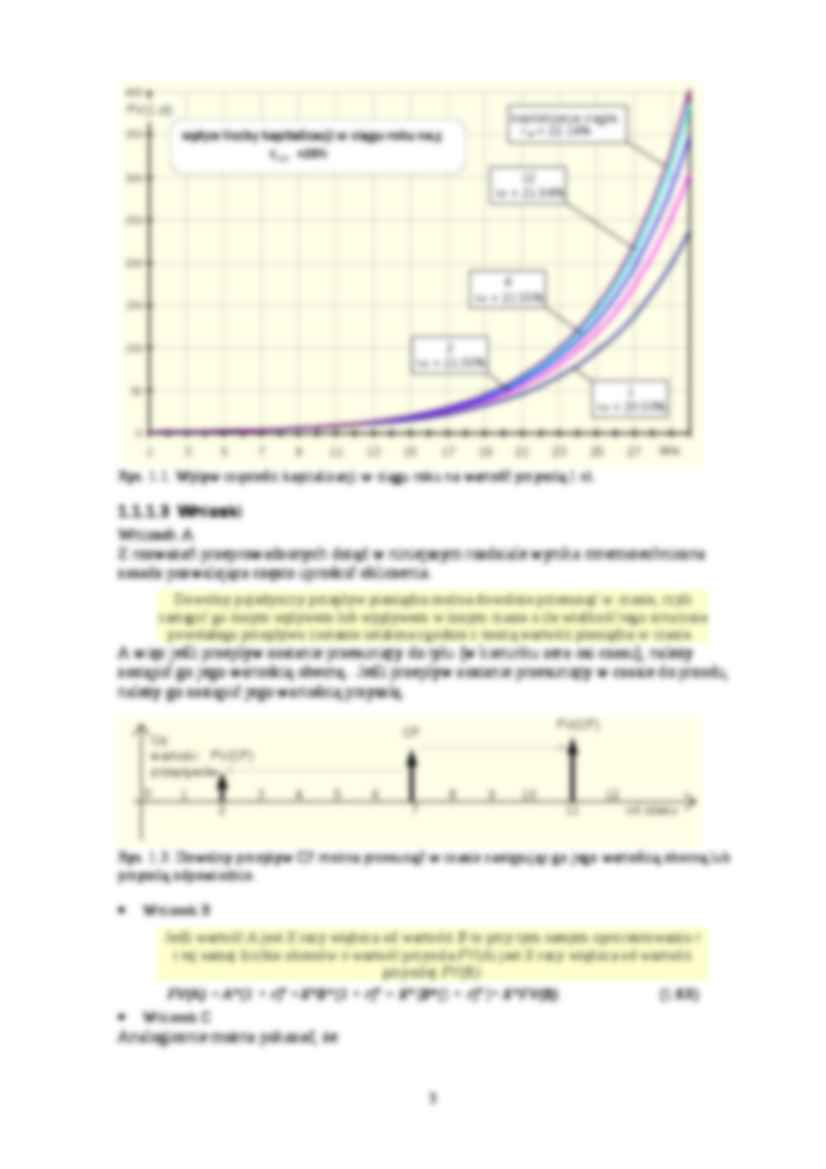
Stopa nominalna Utarło się, iż stopy procentowe podaje się w wartościach nominalnych, w domyśle rocznych (ang. − Annual Percentage Rate − APR ). Stopa nominalna r Nom jest to
r Nom = , gdzie (1.12)
PV − wartość kapitału na początku roku,
FV − wartość kapitału na końcu roku,
oraz okres kapitalizacji jest równy 1 rok.
Jest przyjęte, że oprocentowanie za jeden okres kapitalizacji t kap ustala się ze wzoru:
, gdzie ( 1.13 ) t kap − czas okresu kapitalizacji
t 1rok − czas jednego roku.
Stąd jeżeli liczba okresów kapitalizacji w ciągu roku jest liczbą całkowitą m , to
co po podstawieniu do wzoru 1.13 daje (1.14)
. ( 1.15 ) W zakresie ustalenia długości roku na świecie stosuje się różne ustalenia. W niektórych krajach istnieje dowolność i umowa definiuje długość roku, banki ustalają tę długość na
360 dni lub
365 dni lub
rzeczywistą długość roku kalendarzowego.
W Polsce, po okresie panowania dowolności w tym zakresie, został ustalony dla depozytów bankowych rok rzeczywisty,
dla kredytów bankowych zgodnie z umową kredytową,
dla obligacji rok rzeczywisty,
dla bonów skarbowych rok 360 dniowy.
Stopa efektywna Stopą efektywną nazywa się wielkość
Stopa efektywna= , gdzie
PV − wartość kapitału na początku okresu, dla którego jest liczona stopa efektywna,
FV − wartość kapitału na końcu okresu, dla którego jest liczona stopa efektywna,
oraz okres kapitalizacji jest dowolny, czym różni się ta definicja od definicji stopy nominalnej.
Stopy efektywnej używa się raczej rzadko, ponieważ przy porównywaniu stóp procentowych należy porównywać oprocentowania za ten sam okres. Z tego powodu wprowadzono często używane pojęcie rocznej stopy efektywnej (ang. Effective Annual Rate − EFF ).
, gdzie
PV − wartość kapitału na początku roku, FV − wartość kapitału na końcu roku, oraz okres kapitalizacji jest dowolny.
Jeżeli liczba kapitalizacji w ciągu roku jest równa m , to ze wzoru 1.5 dla czasu jednego roku równego m okresom kapitalizacji i mamy
, czyli
( 1 . 16 ) Zawsze zachodzi nierówność
, ponieważ (1.17)
,
co jest oczywiste jeśli tylko r Nom 0.
Wynika z tego, że kapitalizacja częstsza niż 1 rok zwiększa efektywność oprocentowania i to tym bardziej im większe jest m :
, jeśli m 2 m 1 oraz r Nom 0
Zamiast więc stosowania kapitalizacji częstszej niż roczna można używać stopy efektywnej i kapitalizacji rocznej.
(…)
… opcji. Okres kapitalizacji ciągłej to granica coraz krótszych okresów kapitalizacji: roku, miesiąca, tygodnia, dnia, sekundy, mikrosekundy itd. W granicy uzyskamy odcinek czasu o zerowej długości. Oprocentowanie efektywne przy kapitalizacji ciągłej ref,c uzyskujemy ze wzoru 1.16, przechodząc z liczbą kapitalizacji m w ciągu roku do nieskończoności:
, (1.21)
gdzie liczba e ≈ 2,718 jest podstawą logarytmów naturalnych.
**************
Rozważmy najpierw sytuację inwestora długoterminowego kupującego akcje z zamiarem trzymania ich w nieskończoność - oczekującego dochodu tylko w formie wypłacanych mu corocznie dywidend. W tej sytuacji wychodząc z określenia ceny akcji P0 jako nieskończonej sumy zdyskontowanych dywidend (6.3) i podstawiając za Dt wyrażenie (6.6) otrzymuje się
(1.7)
Oznaczmy
(1.8…
… logarytmów naturalnych.
**************
Rozważmy najpierw sytuację inwestora długoterminowego kupującego akcje z zamiarem trzymania ich w nieskończoność - oczekującego dochodu tylko w formie wypłacanych mu corocznie dywidend. W tej sytuacji wychodząc z określenia ceny akcji P0 jako nieskończonej sumy zdyskontowanych dywidend (6.3) i podstawiając za Dt wyrażenie (6.6) otrzymuje się
(1.7)
Oznaczmy
(1.8…
... zobacz całą notatkę






Komentarze użytkowników (0)