To tylko jedna z 14 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Zadania z kartkówek w latach 2004 – 2006
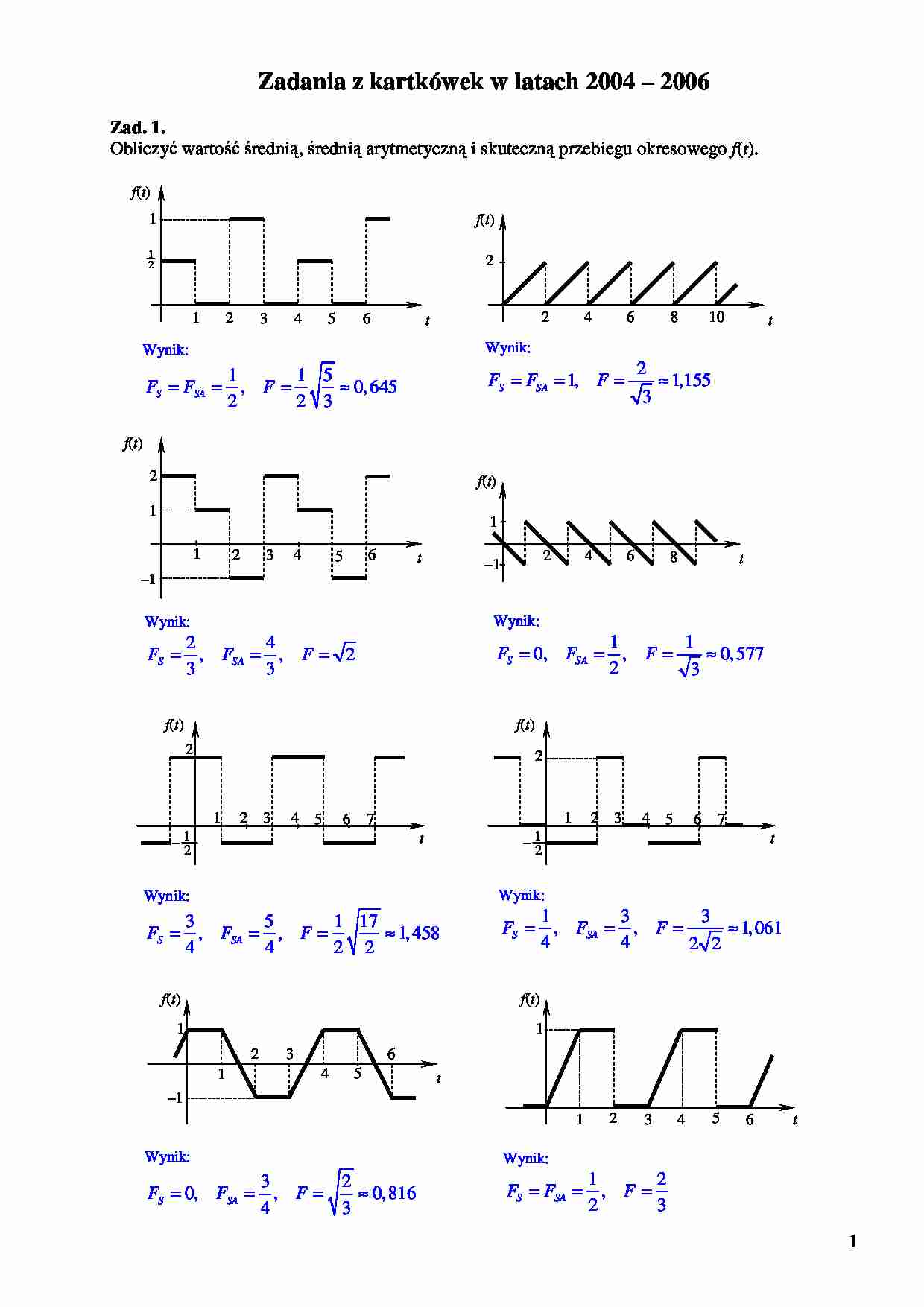
Zad. 1.
Obliczyć wartość średnią, średnią arytmetyczną i skuteczną przebiegu okresowego f(t).
f(t)
1
f(t)
1
2
2
1
2
3
4
5
6
2
t
4
6
Wynik:
FS = FSA = 1, F =
10
t
Wynik:
1
1 5
FS = FSA = , F =
≈ 0, 645
2
2 3
8
2
≈ 1,155
3
f(t)
2
f(t)
1
1
1
2
3
4
6
5
t
2
–1
4
6
8
t
–1
Wynik:
Wynik:
2
4
FS = , FSA = , F = 2
3
3
1
1
FS = 0, FSA = , F =
≈ 0, 577
2
3
f(t)
f(t)
2
2
1
2 3
4 5
6
1
7
−1
2
2 3
4 5
6
7
−1
2
t
t
Wynik:
Wynik:
3
5
1 17
FS = , FSA = , F =
≈ 1, 458
4
4
2 2
1
3
3
FS = , FSA = , F =
≈ 1, 061
4
4
2 2
f(t)
f(t)
1
1
2
1
3
6
4
5
t
–1
1
2
3
Wynik:
5
6
t
Wynik:
3
2
FS = 0, FSA = , F =
≈ 0,816
4
3
4
1
2
FS = FSA = , F =
2
3
1
f(t)
f(t)
„ćwiartka” sinusoidy
„ćwiartka” sinusoidy
1
1
1
2
3
4
0,1
t
0,2
0,3
0,1
t
Wynik:
Wynik:
FS = FSA =
1
1
≈ 0, 318, F =
π
2
FS = FSA =
1
1
≈ 0, 318, F =
π
2
f(t)
f(t)
1
1
1
2
–1
1
2
3
4
5
t
6
1
2
3
4
6
5
Wynik:
Wynik:
3
2
FS = FSA = , F =
≈ 0,816
4
3
t
3
5
FS = FSA = , F =
≈ 0, 559
8
4
f(t)
f(t)
„ćwiartka” sinusoidy
1
1
1
2
3
4
5
6
2
1
t
3
4
t
–1
–1
Wynik:
Wynik:
2
5
FS = 0, FSA = , F =
≈ 0, 745
3
4
FS = 0, FSA =
„połówka” sinusoidy
f(t)
f(t)
1
1
≈ 0,318, F =
π
2
1
1
1
2
3
4
5
6
7
8
1
2
t
Wynik:
FS = FSA =
3
2
2
t
Wynik:
1
1
FS = FSA = , F =
≈ 0,577
2
3
1
1
1
≈ 0, 318, F =
π
2
2
Zad. 2.
Obliczyć transformatę Laplace’a funkcji f(t), F(s) = L{ f(t)}:
f ( t ) = ( t + 1) e−2t 1 ( t − 1)
Wynik:
F (s) =
2s + 5
( s + 2)
e −( s + 2 )
2
f ( t ) = e− t sin t 1 ( t − 1)
Wynik:
F (s) =
( s + 1) sin1 + cos1 − ( s +1)
e
s 2 + 2s + 2
f ( t ) = ( t − 1) e
−( t − 2 )
1 ( t − 3)
Wynik:
( 2s + 3) e2 e−3( s +1)
F (s) =
2
( s + 1)
f ( t ) = t 2e − t 1 ( t − 1)
Wynik:
F (s) =
s 2 + 4s + 5
( s + 1)
(
3
e
−( s +1)
)
f ( t ) = t 2 + 1 e −10t 1 ( t )
Wynik:
F (s) =
s 2 + 20 s + 102
( s + 10 )
3
f ( t ) = ( t − 1) sin 5t 1 ( t )
Wynik:
F (s) = −
5s 2 − 10 s + 125
(s
2
+ 25
)
2
f ( t ) = e −2 t + ( t − 2 ) e − t 1 ( t )
Wynik:
F (s) = −
s 2 + 3s + 1
( s + 2 )( s + 1)
2
3
(
)
f ( t ) = e−2t + t cos t 1 ( t )
Wynik:
F (s) =
s+2
( s + 2)
+1
2
+
s2 −1
(s
2
)
+1
2
=
s 5 + 3s 4 + 6 s 3 + 8 s 2 − 3s − 3
(s
2
)(
)
+ 4s + 5 s 2 + 1
2
f ( t ) = e− t sin 2 t 1 ( t )
Wynik:
F (s) =
( s + 1) ( s
2
2
+ 2s + 5
)
f ( t ) = e−4t 1 ( t ) − 1 ( t − 1)
Wynik:
1 − e −( s + 4 )
F (s) =
s+4
(
)
f ( t ) = ( t − 1) e −2t − e − t 1 ( t )
Wynik:
F (s) =
s2 + s −1
( s + 1) ( s + 2 )
2
(
)
2
f ( t ) = t e−t + 1 1 ( t )
2
Wynik:
F (s) =
1
( s + 2)
2
+
2
( s + 1)
2
+
1 4 s 4 + 16 s 3 + 22 s 2 + 12 s + 4
=
2
2
s2
s 2 ( s + 2 ) ( s + 1)
f ( t ) = t 3 1 ( t − 1)
Wynik:
F (s) =
s 3 + 3s 2 + 6 s + 6 − s
e
s4
f ( t ) = e−2t cos 2 t 1 ( t )
Wynik:
F (s) =
s2 + 4s + 6
( s + 2 ) s 2 + 4s + 8
(
)
4
Zad. 3.
Obliczyć transformatę Laplace’a funkcji impulsowej
... zobacz całą notatkę






Komentarze użytkowników (0)