Wyznaczanie ciepła właściwego ciał stałych

Nasza ocena:

5
Pobrań: 518
Wyświetleń: 2555
Komentarze: 0
Notatek.pl

Pobierz ten dokument za darmo

Pobierz notatkę
Podgląd dokumentu
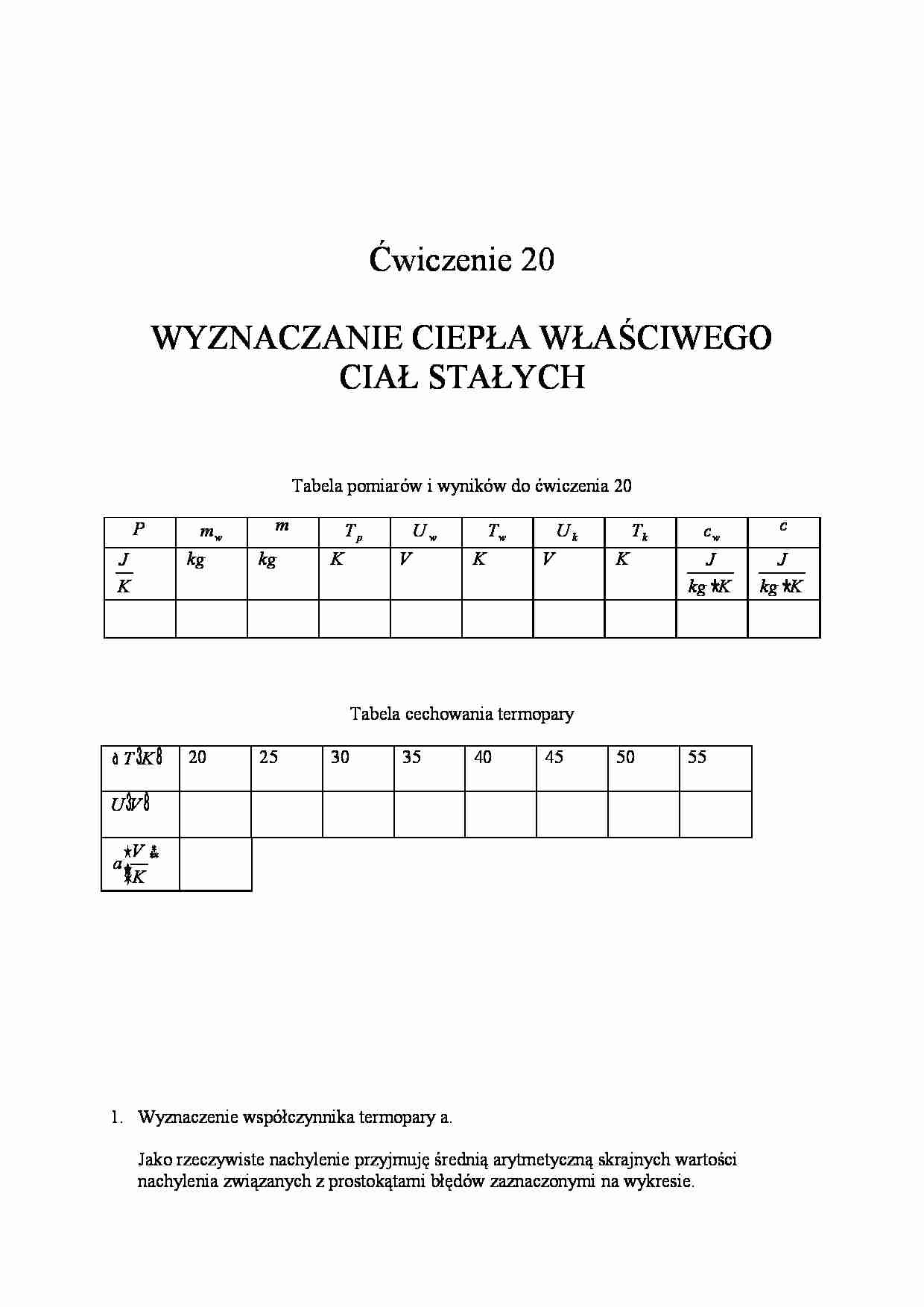
Wyznaczanie ciepła właściwego ciał stałych - strona 1 Wyznaczanie ciepła właściwego ciał stałych - strona 2 Wyznaczanie ciepła właściwego ciał stałych - strona 3

Fragment notatki:


Ćwiczenie 20 WYZNACZANIE CIEPŁA WŁAŚCIWEGO  CIAŁ STAŁYCH Tabela pomiarów i wyników do ćwiczenia 20 P w m m p T w U w T k U k T w c c K J kg kg K V K V K K kg J  K kg J  Tabela cechowania termopary   K T  20 25 30 35 40 45 50 55   V U ≈…     K V a 1. Wyznaczenie współczynnika termopary a. Jako rzeczywiste nachylenie przyjmuję średnią arytmetyczną skrajnych wartości  nachylenia związanych z prostokątami błędów zaznaczonymi na wykresie.                                                   T x T x U y U y T x T x U y U y a a a 1 2 1 2 1 2 1 2 2 1 2 1 2 1   ≈…                                 K V T x x U y y T x x U y y a a a 2 2 2 2 2 1 2 1 1 2 1 2 1 2 1 2 2 1 Wartości odczytane z wykresu wynoszą:    K x 5 , 295 1  ,    K x 5 , 325 2  ,    V y 3 1 10 6 , 0    ,    V y 3 2 10 635 , 1    . Po podstawieniu danych do wzoru otrzymujemy:                                         29 10 125 , 1 31 10 945 , 0 2 1 5 , 0 2 30 10 045 , 0 2 10 035 , 1 5 , 0 2 30 10 045 , 0 2 10 035 , 1 2 1 3 3 3 3 3 3 a ≈…        K V a 3 10 0346 , 0 2. Obliczenie temperatury   w T   oraz  k T  . Przy obliczaniu temperatur skorzystamy ze znajomości stałej termopary:  ≈…        K V a 3 10 0346 , 0 , wykorzystując wzór:  K a U T 273   .       K K K V V K a U T w w 3 , 290 273 10 0346 , 0 10 6 , 0 273 3 3   ≈…                  K K K V V K a U T k k 295 273 10 0346 , 0 10 76 , 0 273 3 3   ≈…

(…)

…, równanie prostej przybliżającej tą zależność można obliczyć stosując metodę regresji
liniowej opartą na rachunku prawdopodobieństwa (metodzie najmniejszych kwadratów).
Mianowicie:
n
 n  n

n xi y i   xi  y i 
i 1
 i  1  i  1  ,
a

n
n


  n  n

 xi2  y i    xi  xi y i 
 i  1  i  1   i  1  i  1
 , gdzie
b

n
2
n 
  n x   xi  .
i 1
 i 1…
…  1465,1 4,7  1321 J 
kg K
72,3   3 373  295
10
72,3   3 78
10

4. Rachunek jednostek.
 J

J 
J
K
  kg 
K

kg K 
J
c  
 K 

kg K
kg kg K



5. Dyskusja błędów.
Za błąd pomiaru temperatury podczas cechowania termopary przyjmujemy  T  0,5K  .
10
Za błąd pomiaru wagi przyjmujemy  m  1   3 kg  .
Błąd pomiaru napięcia obliczamy ze wzoru, biorąc pod uwagę…
... zobacz całą notatkę



Komentarze użytkowników (0)

Zaloguj się, aby dodać komentarz