WYRÓWNANIE SIECI NIWELACYJNEJ METODĄ NAJMNIEJSZYCH KWADRATÓW Z ZASTOSOWANIEM ESTYMACJI LINIOWEJ MODELU PARAMETRYCZNEGO. Dane: I H i [m] i hi A 231,314 1 2,710 B 227,597 2 -4,730 3 -2,013 4 1,111 5 3,120 6 -2,115 7 0,998 ZESTAWIENIE RÓWNAŃ MODELU PARAMETRYCZNOGO Wyznaczenie przybliżonych wartości wysokości H 0 j : H 0 1 = H A - h 1 = 228,604 m H 0 2 = H A + h 2 = 226,584 m H 0 3 = H B - h 6 = 229,712 m Wyznaczenie przybliżonych wartości obser wacji h 0 i : h 0 1 = H A - H 1 = 2,710 m h 0 2 = H 2 - H A = -4,730 m h 0 3 = H 2 - H 1 = -2,020 m h 0 4 = H 3 - H 1 = 1,108 m h 0 5 = H 3 - H 2 = 3,128 m h 0 6 = H B - H 3 = -2,115 m h 0 7 = H 1 - H B = 1,007 m Wyznaczenie wyrazów wolnych modelu L i = h i - h 0 i : Zestawienie ws półczynników modelu parametrycznego. ROZWIĄZANIE MODELU PARAMETRYCZNEGO Rozwiązanie układu równań normalnych. A + = (A T PA) -1 A T P Wyrównanie przybliżonych niewiadomych. Wyrównanie obserwacji na podstawie wyrównanych wysokości. ANALIZA DOKŁADNOŚCI Obliczenie odchyłek δ : Obliczenie estymatora wariancji resztowej:
(…)
…
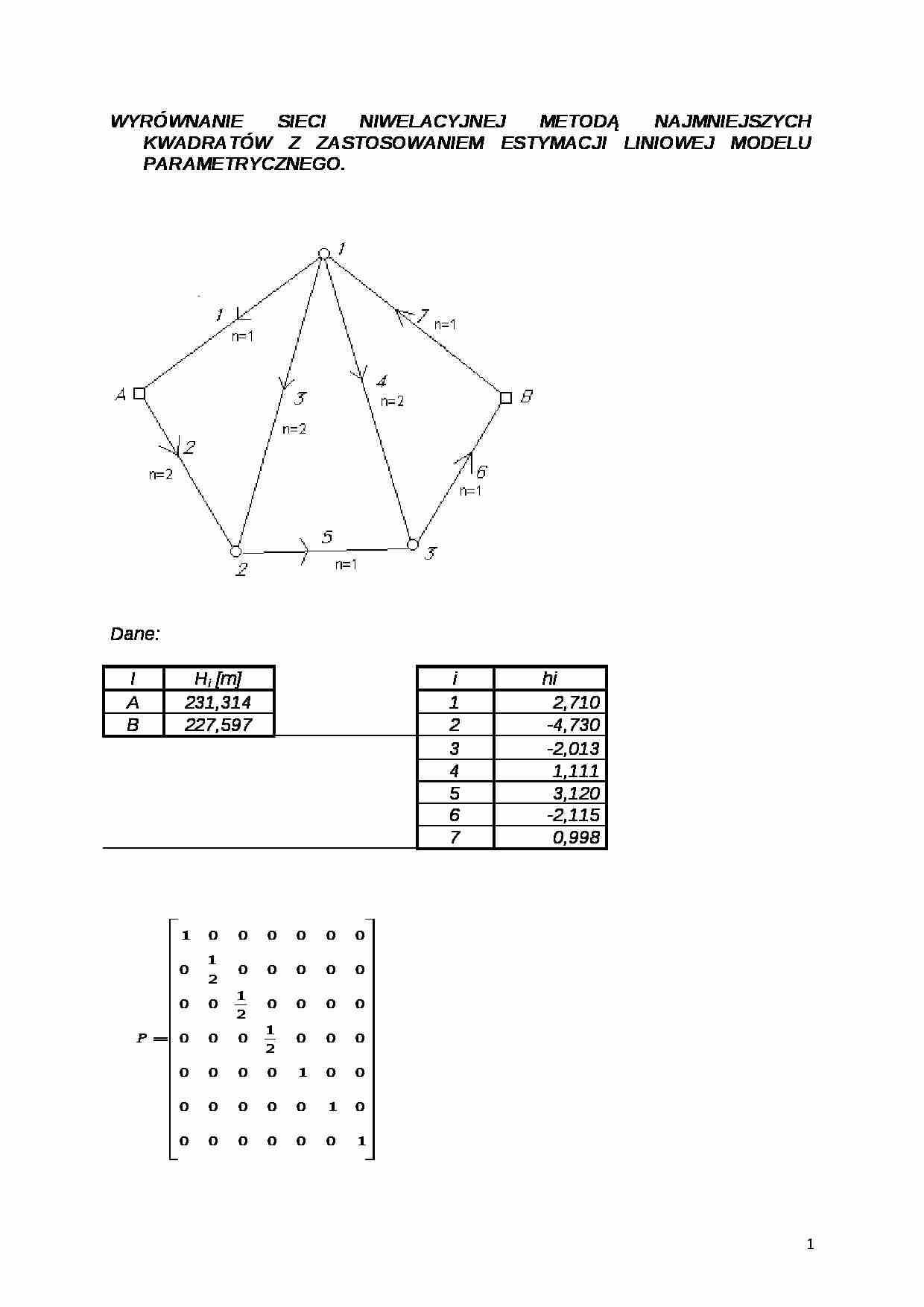
WYRÓWNANIE SIECI NIWELACYJNEJ METODĄ NAJMNIEJSZYCH KWADRATÓW Z ZASTOSOWANIEM ESTYMACJI LINIOWEJ MODELU PARAMETRYCZNEGO.
Dane: I
Hi [m]
i
hi
A
231,314
1
2,710
B
227,597
2
-4,730
3
-2,013
4
1,111
5
3,120
6
-2,115
7
0,998
ZESTAWIENIE RÓWNAŃ MODELU PARAMETRYCZNOGO
Wyznaczenie przybliżonych wartości wysokości H0j :
H01 = HA - h1 = 228,604 m
H02 = HA + h2 = 226,584 m
H03 = HB - h6 = 229,712 m
Wyznaczenie przybliżonych wartości obserwacji h 0i :
h01 = HA - H1= 2,710 m
h02 = H2 - HA= -4,730 m
h03 = H2 - H1= -2,020 m
h04 = H3 - H1= 1,108 m
h05 = H3 - H2= 3,128 m
h06 = HB - H3= -2,115 m
h07 = H1 - HB= 1,007 m
Wyznaczenie wyrazów wolnych modelu Li = hi - h0i :
Zestawienie współczynników modelu parametrycznego.
ROZWIĄZANIE MODELU PARAMETRYCZNEGO
Rozwiązanie układu równań normalnych.
A+ = (ATPA)-1 AT P
Wyrównanie przybliżonych niewiadomych.
Wyrównanie obserwacji na podstawie wyrównanych wysokości.
ANALIZA DOKŁADNOŚCI
Obliczenie odchyłek δ :
Obliczenie estymatora wariancji resztowej:
δTPδ = 26,8313 n-u=4
Wyznaczenie macierzy kowariancji rozwiązań modelu.
- wariancje odpowiednich wysokości Wyznaczenie macierzy kowariancji wyrównanych obserwacji.
- wariancje odpowiednich przewyższeń
Estymacja punktowa dla obliczonych wysokości.
Estymacja punktowa dla przewyższeń.
Estymacja przedziałowa na poziomie ufności p=90%
Model II - rozkład studenta
p=0,90 k= n - u =4
= t(0,95, 4)= 2,132
dla niewiadomych
dla wyrównanych obserwacji
OBLICZENIE ŚREDNIEGO POZIOMU TERENU
Hśr = Hśr = 228,299m.
V(Hśr) = 3,6732 [mm2]
σ(Hśr) = 1,9 mm2
Hśr = 228,299m ± 0,002m
OBLICZENIE WSPÓŁCZYNNIKÓW KORELACJI MIĘDZY WYRÓWNANYMI…
… P
Wyrównanie przybliżonych niewiadomych.
Wyrównanie obserwacji na podstawie wyrównanych wysokości.
ANALIZA DOKŁADNOŚCI
Obliczenie odchyłek δ :
Obliczenie estymatora wariancji resztowej:
δTPδ = 26,8313 n-u=4
Wyznaczenie macierzy kowariancji rozwiązań modelu.
- wariancje odpowiednich wysokości Wyznaczenie macierzy kowariancji wyrównanych obserwacji.
- wariancje odpowiednich przewyższeń
Estymacja…
... zobacz całą notatkę





Komentarze użytkowników (0)