To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


1 ( ) ( ) ( ) ( )( ) 0 0 0 , , 0 0 x x x f x f x f x x b a x x − ′ + ∀ ⇔ ≠ ∧ ∈ ( ) ( ) ( ) ( )( ) 0 0 0 , , 0 0 x x x f x f x f x x b a x x − ′ + ′ ∈ f b a C f Dowód: ( ) ( ) ( ) ( )( ) ( )( ) ( ) ( ) ( )( ) 0 0 0 2 0 0 0 0 0 0 2 , , x x x f x f x f x x c f x x x f x f x f x x b a x x − ′ + − ′ + − ′ + = ≠ ∧ ∈ z czego wynika, e funkcja jest wypukła. Analogicznie: Twierdzenie: ( ) ( 0 , 2
(…)
… WYPUKŁO
Nadwykres funkcji f:
{
N f := (x, y ), x ∈ D f , y ≥ f (x ) }
A ⊂ R n - nazywamy zbiorem wypukłym, je li dla ka dych dwóch punktów nale cych
do A – odcinek je ł cz cy jest zawarty w A.
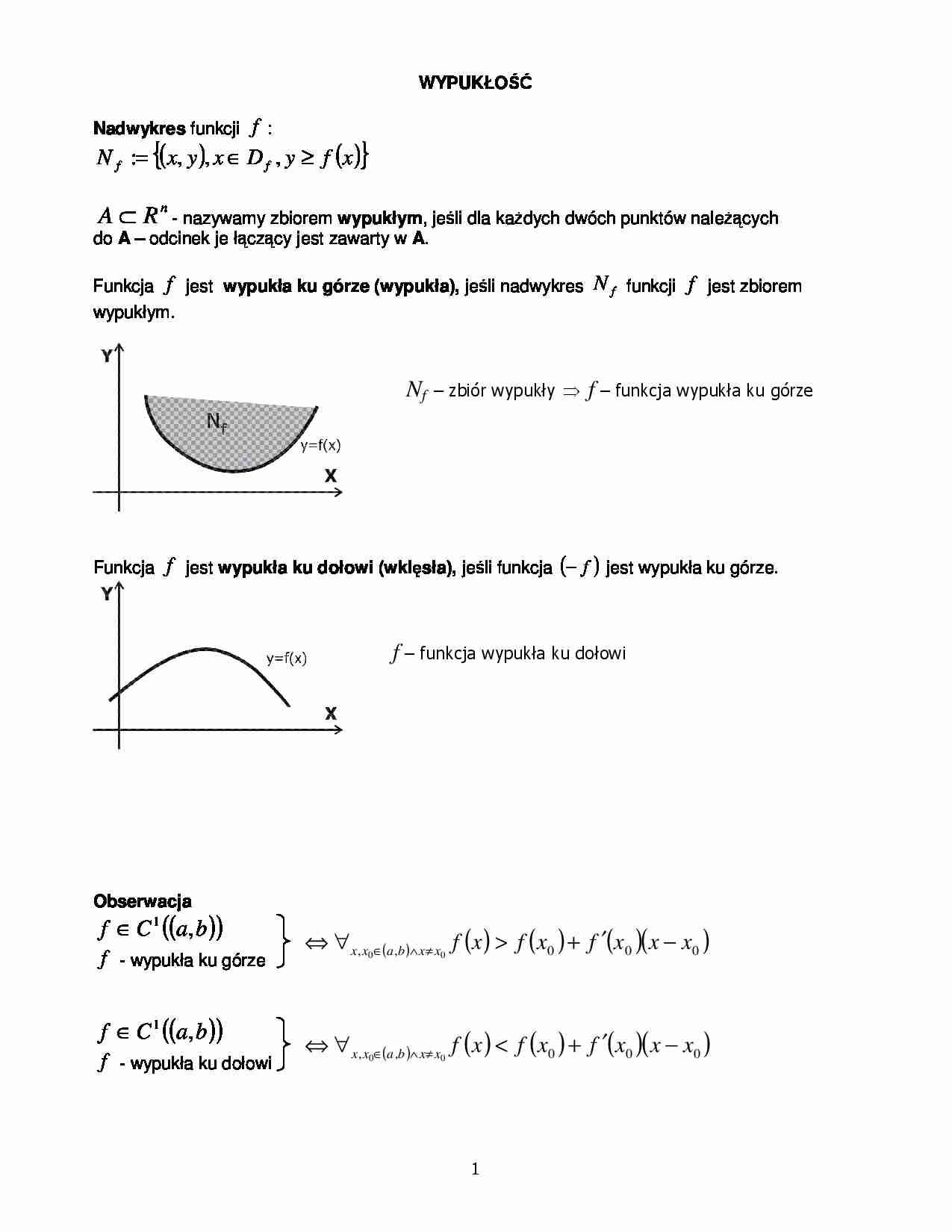
Funkcja f jest wypukła ku górze (wypukła), je li nadwykres N f funkcji f jest zbiorem
wypukłym.
Nf f
Funkcja f jest wypukła ku dołowi (wkl sła), je li funkcja (− f ) jest wypukła ku górze.
f
Obserwacja
f…
... zobacz całą notatkę






Komentarze użytkowników (0)