To tylko jedna z 20 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

WYPŁYWY PRZEZ OTWÓR I PRZYSTAWKI
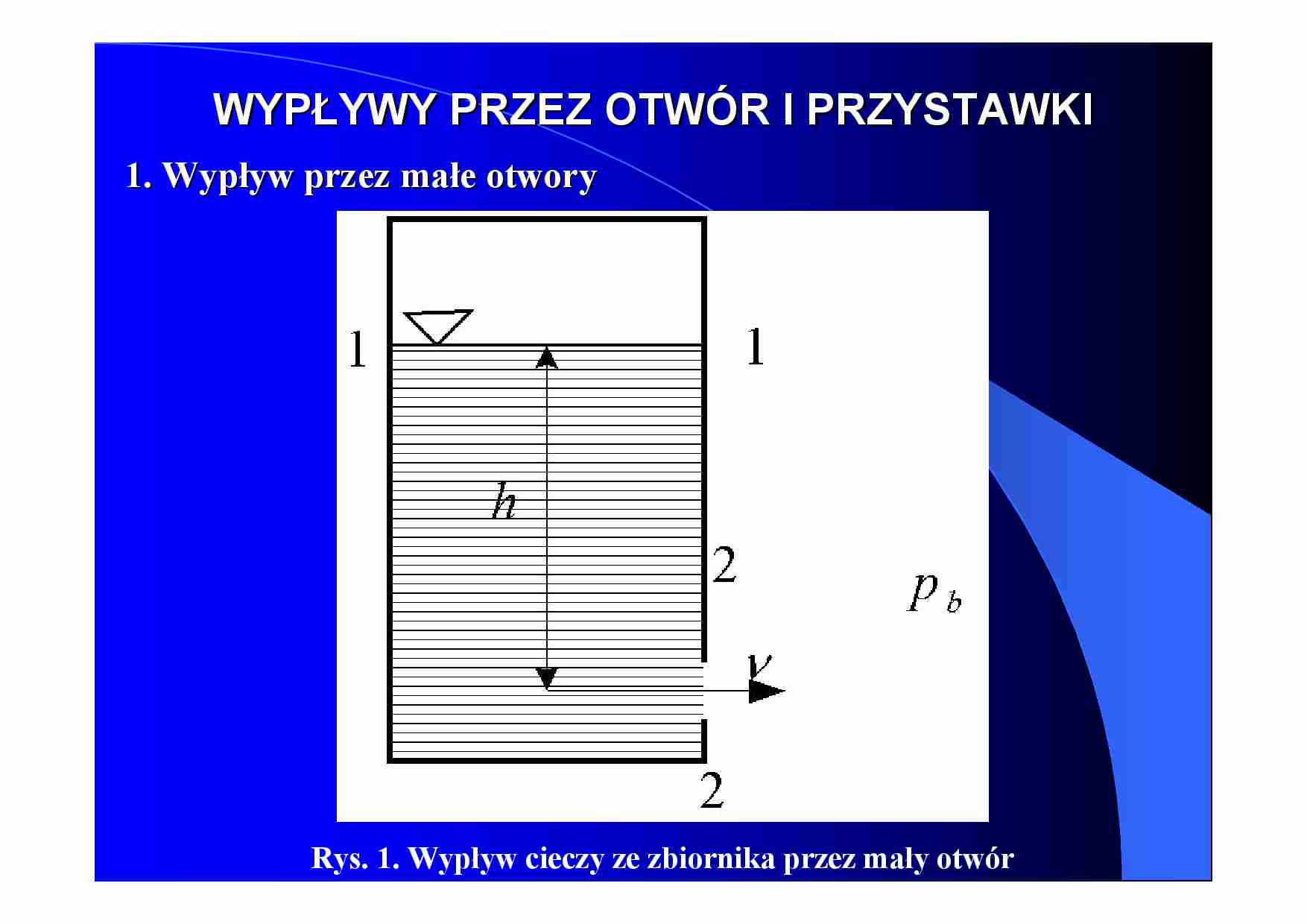
1. Wypływ przez małe otwory
Rys. 1. Wypływ cieczy ze zbiornika przez mały otwór
Z równania Bernoulliego dla przekroju 1-1 i 2-2 otrzymamy:
pn + pb
pb ν 2
+h =
+
,
ρg
ρ g 2g
(1)
skąd
⎛p
⎞
ν = 2g ⎜ n + h ⎟.
⎝ ρg
⎠
(2)
Dla zbiornika otwartego, gdy pn = 0, a p=pb otrzymujemy zwór Torricellego w
postaci:
ν = 2gh.
(3)
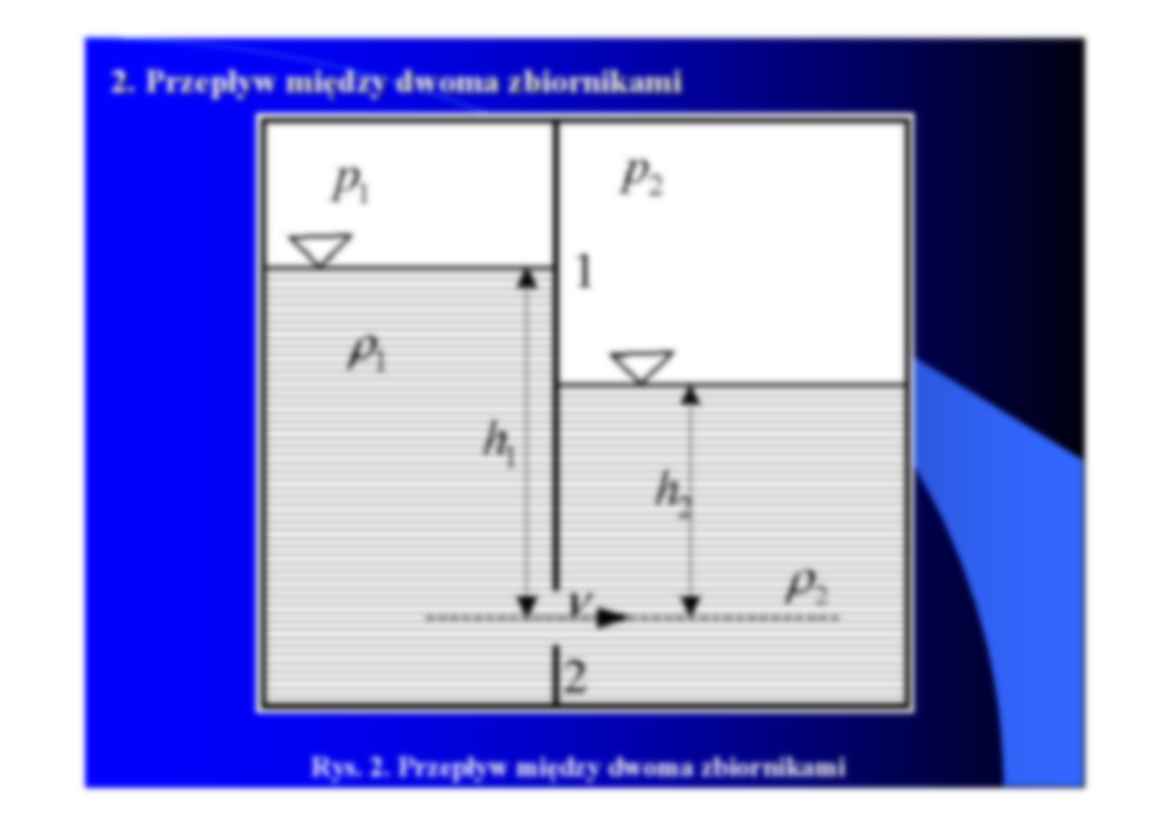
2. Przepływ między dwoma zbiornikami
Rys. 2. Przepływ między dwoma zbiornikami
Równanie Bernoulliego dla przekroju 1-1 i 2-2 przybiera postać
p1
p2 + ρ2gh2 ν 2
+ h1 =
+
,
2g
ρ1g
ρ1g
(4)
skąd
⎡ p1
p2 + ρ2gh2 ⎤
ν = 2g ⎢
+ h1 −
⎥.
ρ1g
ρ1g
⎣
⎦
(5)
Rzeczywista prędkość wypływu jest mniejsza od teoretycznej ze względu na
opory wypływu i wynosi:
ν r = ϕν
Współczynnik ϕ , jest współczynnikiem prędkości, i ma wartość zależną o
liczby Reynoldsa (Tabela 1.).
(6)
Rys. 3. Formowanie się strugi cieczy podczas wypływu przez otwór o ostrych
krawędziach
Wskutek oddziaływania na cząstki płynu sił bezwładności struga ulega
zwężeniu (kontrakcji), a ciśnienie osiąga wartość ciśnienia otoczenia właśnie w
miejscu maksymalnego przewężenia, gdzie występuje prędkość określona
wzorem (2), to rzeczywisty strumień wypływu wynosi:
qvr = ν r A c = ϕκν A,
gdzie: κ = A c A - jest współczynnikiem kontrakcji,
kontrakcji
µ = ϕκ - współczynnikiem wypływu.
Tabela 1.
(7)
3. Przystawki – ssące działanie strugi
Rys. 4. Wypływ cieczy ze zbiornika przez przystawkę walcową
Równanie Bernoulliego dla przekroju 1-1 i 2-2 przybiera postać
2
2
pb ν 2
p1 ν 1
+
=
+
,
ρ g 2g ρ g 2g
(8)
a równanie ciągłości
2
⎛ d2 ⎞
πd
πd
= ν2
⇒ ν1 = ν1 ⎜ ⎟ .
ν1
4
4
⎝ d1 ⎠
2
1
2
2
(9)
Po podstawieniu (9) i (8) i wyznaczeniu p1 otrzymamy
⎛ ⎛ d ⎞4
⎞
ρν
2
⎜ ⎜ ⎟ − 1⎟ ,
p1 = pb −
⎟
2 ⎜ ⎝ d1 ⎠
⎝
⎠
2
2
gdzie ν 2 = ϕ 2gh.
(10)
Wartość współczynników ϕ , κ , µ dla różnych przystawek przedstawiono
w tabeli 2.
4. Wypływ ustalony cieczy przez duży otwór
Rys. 5. Wypływ przez duży otwór
Prędkość wypływu cieczy w odległości z od zwierciadła określa wzór
Torricellego
ν = 2gz.
(11)
Przez elementarną powierzchnię
dA = b ( y ) dy = b ( z )
dz
,
sin α
(12)
Wypływa ciecz o elementarnym strumieniu objętości
dqv =
b (z)
sin α
2gzdz.
(13)
Strumień objętości wypływającej przez powierzchnię A wynosi
2g
qv = µ ∫ dqv = µ
sin α
A
h2
∫ b (z)
h1
zdz.
(14)
Dla otworu prostokątnego w pionowej ścianie
b ( z ) = b = const, sinα =1, zatem
h2
qv = µb 2g ∫
h1
(
3
3
2
2
zdz = µb 2g h2 − h1 2
3
)
(15)
Dla b ( z ) = b = const, sinα =1, h1 = 0, h2 = h otrzymamy wzór dla
przelewu
2
qv = µbh 2gh.
3
Rys. 6
(16)
Rys. 7. Charakterystyka przepływu przelewu
5. Czas wypływu przez mały otwór
Rys. 8. Wypływ przez mały otwór
Chwilowy strumień objętości cieczy wypływającej wynosi
Q ( z ) = µ A0 2gh.
(17)
Z porównania objętości cieczy wypływającej w czasie dt otrzymamy
µ A0 2gzdt = −A ( z ) dz
skąd
dt =
a czas wypływu
h2
t = −∫
h1
A ( z ) dz
µ A0 2gz
A ( z ) dz
µ A0 2gz
=
h1
,
(19)
A ( z ) dz
∫ µA
h2
(18)
0
2gz
(20)
6.
(…)
… 2gz
=
h1
,
(19)
A ( z ) dz
∫ µA
h2
(18)
0
2gz
(20)
6. Wypływ gazu przez otwór zaokrąglony
Rys. 9. Wypływ gazu
Załóżmy, że wypływ odbywa się przy przemianie adiabatycznej (bez wymiany
ciepła ) więc proces rozprężania opisuje równanie
p0
p
= κ
κ
ρ0
ρ
Równanie Bernoulliego przybiera wówczas postać
ν2
κ
+
p
2 κ −1 ρ
zatem dla wypływu ze zbiornika
κ
p0
κ − 1 ρ0
=
ν2
2
(25)
= const,
+
κ
p
κ −1 ρ
,
(26…
... zobacz całą notatkę






Komentarze użytkowników (0)