To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


WYKŁAD 5_1
Przemiany fazowe I-go rodzaju – równanie Clausiusa-Clapeyrona.
1. G=f(p,T) - przypomnienie.
dG=dH-TdS-SdT
dG=dU+pdV+Vdp-TdS-SdT
dG=TdS-pdV+pdV+Vdp-TdS-SdT
ZałoŜenia: -przemiana pVT jednej ściśle określonej fazy i to przemiana odwracalna
- praca tylko objętościowa
dG=Vdp-SdT
∂G
∂G
∂G
∂G
dG =
⇒
∂p dp + ∂T dT
∂p = V oraz ∂T = −S
p
p
T
T
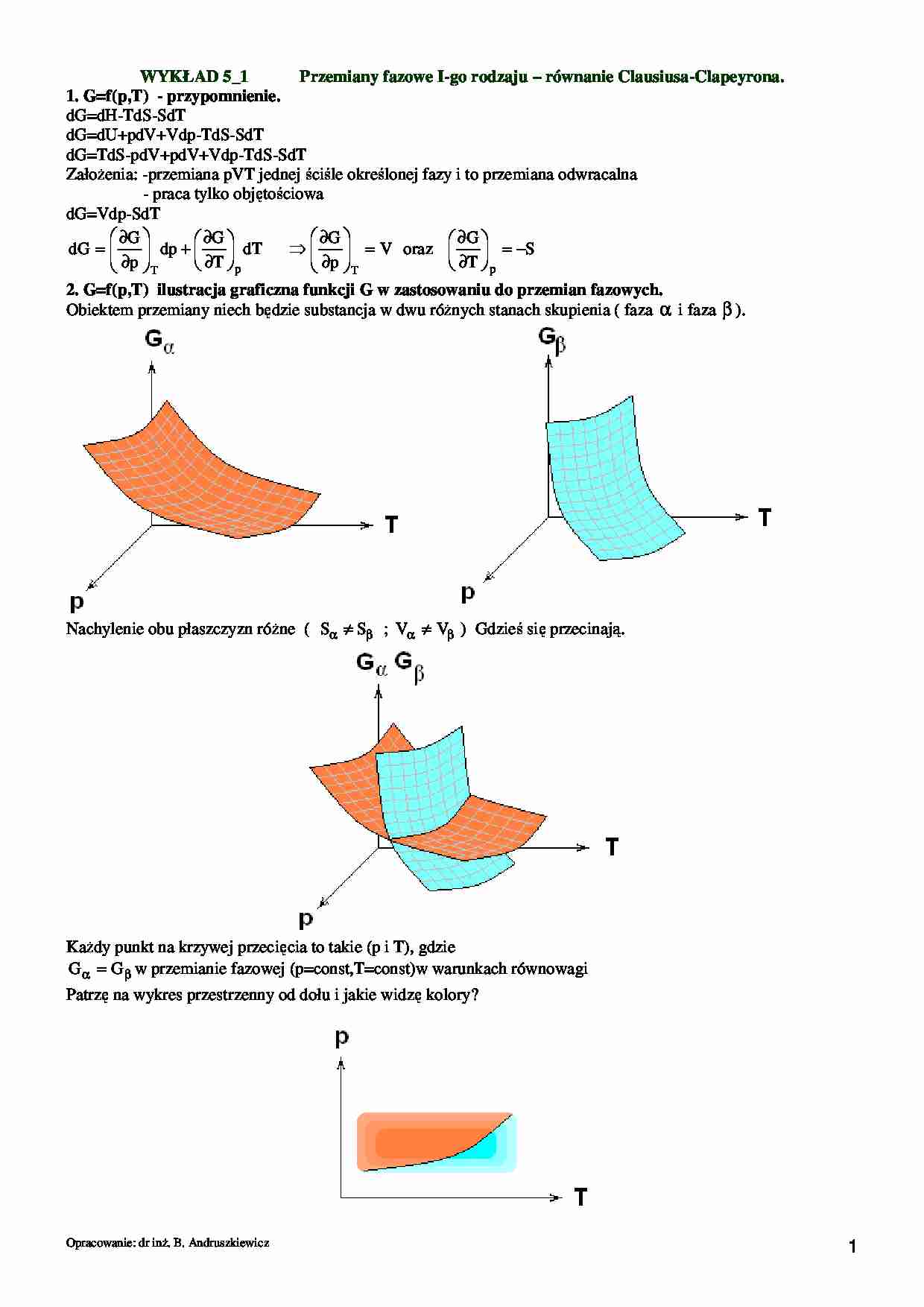
2. G=f(p,T) ilustracja graficzna funkcji G w zastosowaniu do przemian fazowych.
Obiektem przemiany niech będzie substancja w dwu róŜnych stanach skupienia ( faza α i faza β ).
Nachylenie obu płaszczyzn róŜne ( Sα ≠ Sβ ; Vα ≠ Vβ ) Gdzieś się przecinają.
KaŜdy punkt na krzywej przecięcia to takie (p i T), gdzie
G α = G β w przemianie fazowej (p=const,T=const)w warunkach równowagi
Patrzę na wykres przestrzenny od dołu i jakie widzę kolory?
Opracowanie: dr inŜ. B. Andruszkiewicz
1
3. Wyprowadzenie równania Clausiusa-Clapeyrona.
RozwaŜam dwa bliskie stany równowagi
czyli dwa bliskie punkty na krzywej
Krzywe te dzielą płaszczyznę (p,T) na trzy obszary –
równowagi.
trwałości fazy stałej, trwałości fazy ciekłej i trwałości fazy
G α = G β pierwszy punkt na krzywej
gazowej.
G α + dG α = G β + dG β drugi, bliski
pierwszemu punkt na krzywej
Zgodnie z rozwaŜaniami (p. 1 wykładu)
G α + Vα dp − SεdT = G β + Vβdp − SβdT
Vα dp − Sε dT = Vβdp − SβdT
Porządkuję według zmiennych
Vα dp − Vβdp = Sα dT − SβdT
(
(
)
)
Sα − Sβ
dp
=
dT
Vα − Vβ
dp ∆S
=
;
dT ∆V
czyli
a
skoro kaŜda przemiana fazowa jest izobaryczna
to
∆H pf
dp
=
dokładne równanie na
dT T ∗ ∆Vpf
krzywą równowagi fazowej
( parowania, topnienia lub sublimacji).
4. Nachylenie krzywych równowagi.
FAZY
NAZWA PRZEMIANY
∆H pf
∆Vpf
dp/dT
ciecz-para
parowanie
+
+
+
para-ciecz
skraplanie
-
-
+
ciało stałe-gaz
sublimacja
+
+
+
gaz-ciało stałe
resublimacja
-
-
+
ciało stałe-ciecz
topnienie
+
+(-)
+(-)
ciecz-ciało stałe
krzepnięcie
-
-(+)
+(-)
ciało stałe-ciało stałe
?
?
?
róŜnie
5. Krzywa parowania - scałkowane równanie Clausiusa-Clapeyrona.
dp ∆Spar
=
dT ∆Vpar
a)Przyjmuję, Ŝe ∆Spar =
∆H par
T
bo przemiana fazowa biegnie przy T=const i przy p=const
b)Przyjmuję, Ŝe ∆Vpar = Vpary − Vciecz ≈ Vpary
objętość cieczy jest pomijalnie mała w porównaniu z objętością pary.
RT
para jest gazem doskonałym.
c)Przyjmuję, Ŝe Vpary =
p
Wracając do równania wyjściowego:
Opracowanie: dr inŜ. B. Andruszkiewicz
2
dp ∆H par ∗ p
dp ∆H par ∗ dT
=
⇒
=
2
dT
p
RT
RT 2
Wykonuję całkowanie, gdy stanem początkowym jest punkt 1 na krzywej parowania ( p1 , T1 )
a stanem końcowym inny, niezbyt oddalony, punkt 2 na krzywej parowania ( p2 , T2 ).
Zakładam przy tym, Ŝe entalpia parowania nie zmienia się z temperaturą.
∆H par 1
p
1
ln 2 = −
∗ −
T
p1
R
2 T1
6. Parowanie kropel o róŜnych promieniach - WZÓR KELVINA
p
2 γ Vciecz
ln r =
∗
p∞
r
RT
gdzie pr pręŜność pary nad powierzchnią o promieniu krzywizny r
(dodatnim dla kropel, ujemnym dla powierzchni pęcherzyka pary wewnątrz cieczy)
p∞ pręŜność
(…)
… o promieniu krzywizny r
(dodatnim dla kropel, ujemnym dla powierzchni pęcherzyka pary wewnątrz cieczy)
p∞ pręŜność pary nad płaską powierzchnią - promień krzywizny nieskończenie duŜy,
γ napięcie powierzchniowe cieczy mierzone w N/m lub w J/m2 .
2γ
= ∆p wzniesienie kapilarne,
r
Vciecz objętość molowa cieczy.
Przykładowo:
dla wody w temp.298K γ = 0,07275Nm −1
18,1g ∗ m3
m3
mol
mol ∗ 106 g
pręŜność pary…
…-desorpcja ale z takim ciałem stałym, które ma tylko pory
otwarte z obu stron (rurki). Wzór opisujący przebieg desorpcji (parowania) róŜni się współczynnikiem 2 od wzoru
opisującego adsorpcję (wykraplanie).
Opracowanie: dr inŜ. B. Andruszkiewicz
4
Najpierw wypełnią się cieczą pory maleńkie, dla których pr najmocniej róŜni się od p∞ .
Potem wypełnia się pory o duŜym promieniu
W czasie odpompowywania (desorpcja, odparowywanie z pełnych początkowo porów)
paruje ciecz z menisków kulistych, chociaŜ pory są cylindryczne!
Wobec tego uzyskane krzywe (ilość cieczy w zaleŜności od pręŜności pary) adsorpcji i desorpcji
nie będą się pokrywały.
Wzór Kelvina jest podstawą pomiarów ilości porów i ich średnic i jeszcze dodatkowo pozwala mierzyć jaką
częścią wszystkich są pory otwarte obustronnie.
8. Przemiany fazowe…
… kolejno wypełniać się będą pory większe.
Teraz poprowadzimy doświadczenie w drugą stronę - stopniowo obniŜając pręŜność pary (wypompowywanie).
Ciecz obecna w porach będzie wrzała.
Zacznie się to oczywiście najpierw w porach duŜych,
a ostatnie porcje wypompowywanej pary pochodzić będą z
najmniejszych porów, gdzie siły trzymające uciekające cząsteczki
są największe.
ADSORPCJA (kondensacja) PRZY PORACH…
... zobacz całą notatkę






Komentarze użytkowników (0)