Wykład - nadwyższka temperatury pręta w stosunku do temperatury otoczenia

Nasza ocena:

3
Pobrań: 21
Wyświetleń: 952
Komentarze: 0
Notatek.pl

Pobierz ten dokument za darmo

Pobierz notatkę
Podgląd dokumentu
Wykład - nadwyższka temperatury pręta w stosunku do temperatury otoczenia - strona 1 Wykład - nadwyższka temperatury pręta w stosunku do temperatury otoczenia - strona 2 Wykład - nadwyższka temperatury pręta w stosunku do temperatury otoczenia - strona 3

Fragment notatki:

WYKŁAD 4
 - nadwyższka temperatury pręta w stosunku do temperatury otoczenia;
Wartość nadwyższki temperatury na końcu pręta wyraża się wzorem:
 L  0
1
ch(mL)
Strumień ciepła doprowadzony do pręta wyraża się wzorem:
d
x 0
dx
d
shmL  x    m 
 0
dx
ch (mL)
*
Q  x 0   A  
*
Q  x 0   A     0 (m)  tgh(mL)  A     0  m  tgh (mL)
*
Q  x 0   0 O    A    tgh (mL)

 
zawsze
od 1
mniejszy
20
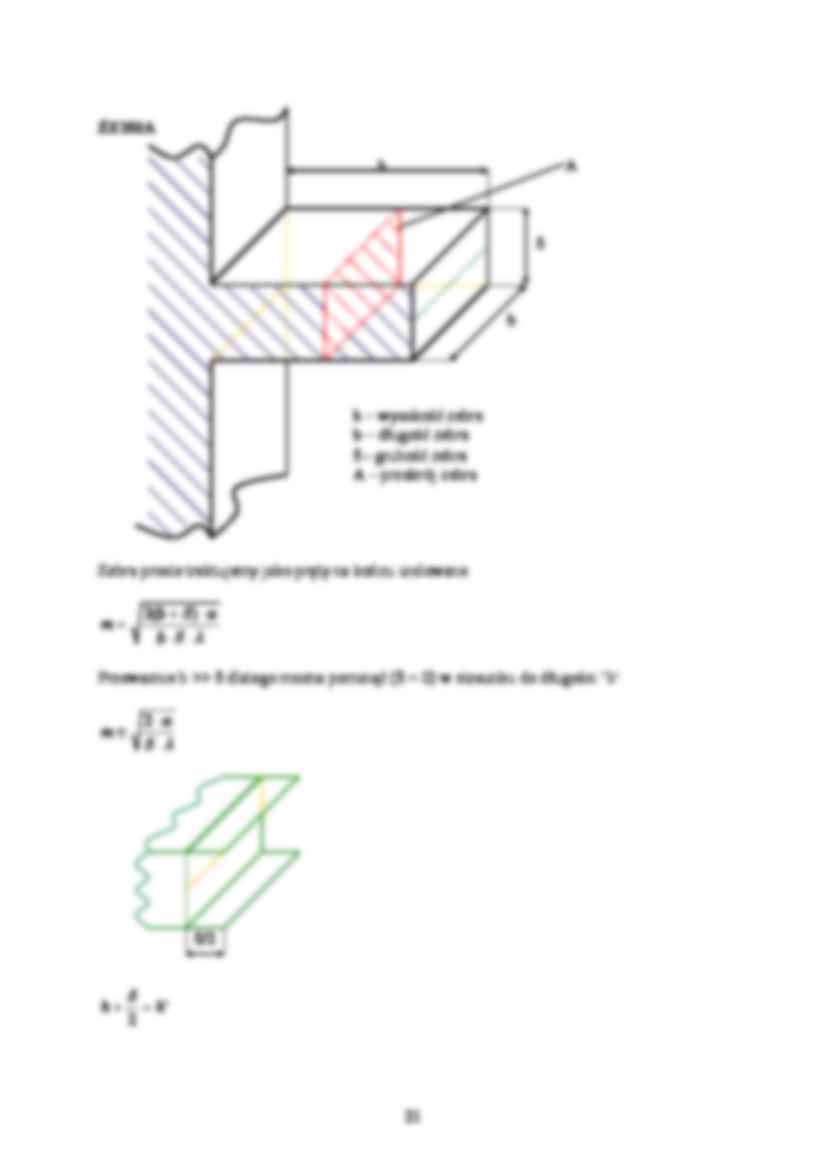
ŻEBRA
h
A

b
h – wysokość żebra
b – długość żebra
 - grubość żebra
A – przekrój żebra
Żebra proste traktujemy jako pręty na końcu izolowane.
2(b   )  
b   
m
Przeważnie b  dlatego można pominąć ( = 0) w stosunku do długości ‘b’.
2 
 
m
/2
h

2
 h'
21
POWIERZCHNIE OŻEBROWANE
h
t1, 1
A1Ż
1
A1

b
A1OŻ
2
s
s
s
m
t2, 2
s
-
powierzchnia żebra i powierzchnia między żebrowa
-
powierzchnia nałożenia żebra
-
powierzchnia żebra
s – podziałka żeber (odległość między żebrami)
s – grubość ścianki
m – średnia temperatura żebra
n – ilość żeber
Dla jednego żebra:
*
1)
Q 1  A1   1 (t1 1 )
2)
Q 1  A1
*
1  2
s
s
22
*
Q 1  ( A1OŻ  A1Ż )   2 ( 2  t 2 )  A1Ż   2 ( m  t 2 ) 
3)
  1   Ż ( 1   2 )  A1Ż  ( A1OŻ  A1Ż )   2 ( 2  t 2 ) 
  A1OŻ  A1Ż   A1Ż   Ż    2 ( 2  t 2 ) 


A
A
 A1OŻ 1  1Ż  1Ż   Ż    2 ( 2  t 2 ) 
 A1OŻ A1OŻ

 A1OŻ   OŻ   2 ( 2  t 2 )
gdzie:
Ż 
 m  t2 m
- sprawność żebra

 2  t2 2

 OŻ  1 


A1Ż
(1   Ż ) - sprawność powierzchni żebra
A1OŻ

Z powyższych równań wynikają zależności:
*
1)
Q 1
t1   1  1 
A1  1
2)
Q 
1  2  1  s
A1  s
3)
Q
1
 2  t2  1 
A1OŻ  OŻ   2
*
*
Stopień ożebrowania powierzchni:

A1OŻ
A
 OŻ
A1
A
Po zsumowaniu stronami otrzymamy wyrażenie:
*

Q  1 
1

t1  t 2  1   s 
A1   1  s    OŻ   2 


Po przekształceniu wyrażenia otrzymamy wzór na strumień ciepła przekazywany przez
ściankę ożebrowaną:
t1  t 2
*
QC  A
1
1

s
1

 s    OŻ   2
23
Sprawność żebra prostego:
*
Ż 

Q
 m  t 2  m   2  A1Ż

 *0 
 2  t 2  2   2  A1Ż Q
) MAX
2
O  2
 tgh (mh)
  1
A

  tgh (mh) 
 2   2  A1Ż
2  2 h
tgh (mh)
mh
Ż
1
wykres sprawności żebra prostego
mh
Żebra o innych kształtach – sprawność dobiera się z gotowych wykresów.
Żebra stosujemy, gdy są duże różnice współczynników 1 i 2 w celu zwiększenia wymiany
ciepła.
1, 1, Ż1
2, 2, Ż2
Ogólny wzór ma postać:
t1  t 2
*
QA
1
1   1OŻ   1

s
1

 s  2   1OŻ   2
24
WYBRANE ZAGADNIENIA PRZEWODZENIA CIEPŁA
PRZEWODENIE CIEPŁA Z WEWNĘTRZNYMI ŹRÓDŁAMI CIEPŁA
Dla ścianki płaskiej

1
 = idem
qx
qv = idem
qx+dx
dQv
2
x
dx

Źródła ciepła:
*
W 
 m 3  - gęstość źródeł ciepła
 
Q
qv  v
V
*
d Qx
Q x  dx  Q x 
 dx
dx
*
d
Q x   A  
dx
*
*
*
*
Q x  dQ v  Q x  dx
*
*
d Qx
d 2
 A  2
dx
dx
*
d Q v  A  dx  q v ... zobacz całą notatkę



Komentarze użytkowników (0)

Zaloguj się, aby dodać komentarz