To tylko jedna z 13 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Wielomian jednej zmiennej – funkcja określona wzorem f(x)=anxn + an-1xn-1 + ... + a1x + a0 gdzie an, an-1,..., a1, a0 są danymi liczbami, wykładnik n jest liczbą naturalną. Wielomian jest sumą jednomianów. Przedstawienie wielomianu w postaci sumy jednomianów może nie być jednoznaczne, gdy niektóre jednomiany mają ten sam stopień. Wykonuje się wtedy redukcję wyrazów podobnych, polega ona na zastąpieniu jednomianów podobnych jednym jednomianem będącym ich sumą i przedstawia się wielomian w takiej postaci, w której każde dwa jednomiany mają różne stopnie. Współczynniki kolejnych jednomianów nazywa się współczynnikami wielomianu, maksymalny stopień jednomianu – stopniem wielomianu. Stopień wielomianu - maksymalny stopień jednomianu, oznacza się go st f(zgodnie z określeniem stopnia jednomianu wielomian stały, ale niezerowy ma stopień 0, wielomian zerowy nie ma stopnia). Wielomian zerowy - jest to funkcja stała W(x) = 0. Wielomian zerowy nie ma określonego stopnia. Równość wielomianów – dwa wielomiany są równe wtedy i tylko wtedy, gdy mają równe stopnie oraz równe współczynniki przy jednomianach tych samych stopni, a więc wtedy i tylko wtedy, gdy ciągi współczynników tych wielomianów są równe. Pierwiastki wielomianu – miejsca zerowe wielomianu, liczby dla których dany wielomian przyjmuje wartość zero. Ważną charakterystykę pierwiastków wielomianów podaje twierdzenie Bezout. Pierwiastek wielokrotny wielomianu - Liczbę r nazywamy k - krotnym pierwiastkiem wielomianu W(x) stopnia n (k, n N i k n) wtedy i tylko wtedy, gdy wielomian W(x) jest podzielny przez (x - r)k i nie jest podzielny przez (x - r)k+1 Działania na wielomianach – w zbiorze wielomianów określa się działania dodawania i mnożenia. Wielomiany dodaje się tak jak liczby, po dodaniu grupuje się odpowiednie składniki. Sumą wielomianu jest wielomian którego współczynniki otrzymuje się przez dodanie współczynników jednomianów tego samego stopnia. W zbiorze wielomianów określa się też działanie odwrotne do dodawania tj. odejmowanie. Odejmowanie wielomianów sprowadza się do dodawania wielomianów, którego współczynniki otrzymuje się ze współczynników odejmowanego wielomianu po zamianie znaków na przeciwne. Wielomiany mnoży się tak jak liczby, po wymnożeniu grupuje się odpowiednie składniki. Iloczynem wielomianu jest wielomian, którego współczynniki otrzymuje się mnożąc kolejno każdy jednomian pierwszego wielomianu przez każdy jednomian drugiego wielomianu, a następnie wykonując redukcję wyrazów podobnych. W zbiorze wielomianów nie jest określone działanie odwrotne do mnożenia tj. dzielenie.
(…)
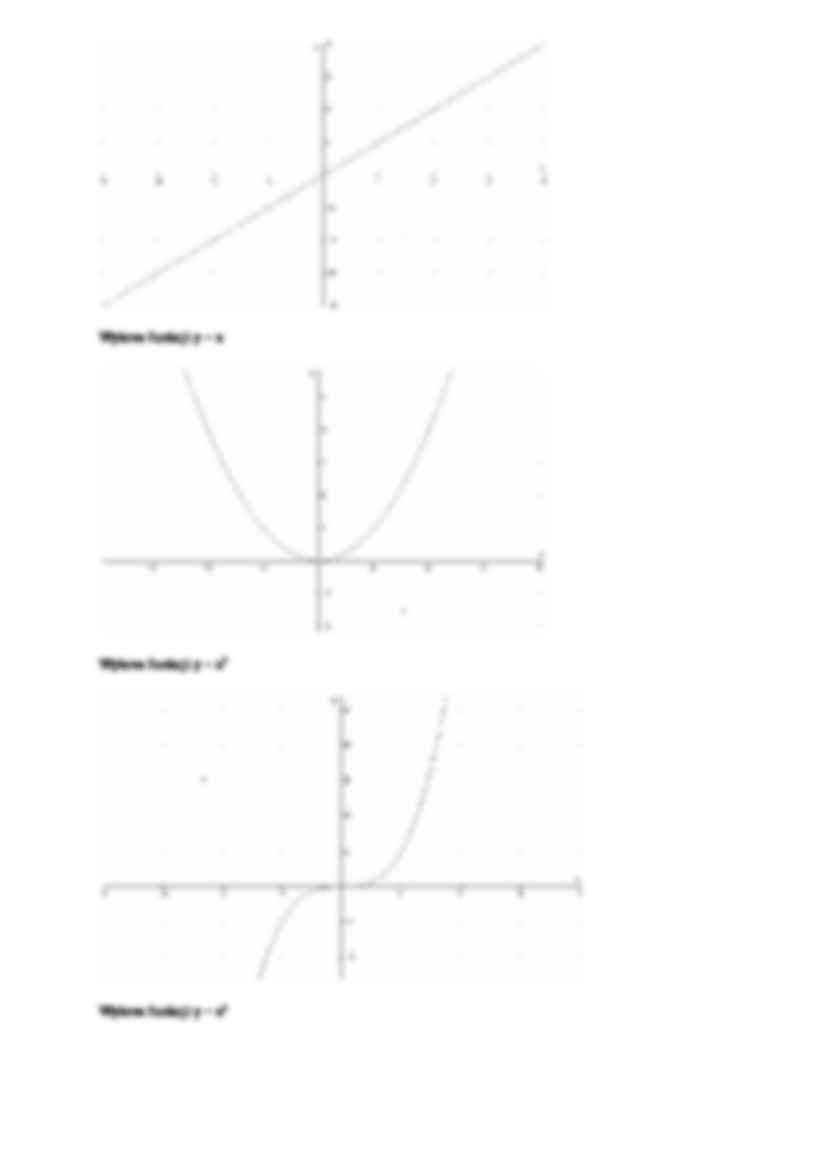
…. Wykres jest symetryczny
względem osi OY gdy p = 0.
Wzory Wiete'a - między pierwiastkami x1, x2 równania kwadratowego, a jego współczynnikami zachodzą związki: x1 +
x2= -b/a, x1x2=c/a.
ZADANIA
Twierdzenie 1: Jeżeli
, to reszta z dzielenia
dwumian
równa jest
Wniosek (twierdzenie Bezout)
.
Twierdzenie 2: Jeżeli liczba wymierna
jest miejscem zerowym (pierwiastkiem) wielomianu
o współczynnikach całkowitych…
…
Odpowiedźx należy do (-?,-7) (-7,-1) (2, ?)
? - nieskończoność
FUNKCJE
Funkcja liniowa
Wykres funkcji liniowej
Funkcja liniowa - jest to funkcja f określona wzorem f(x) = ax + b, gdzie a,b są ustalonymi liczbami. Liczba a jest
nazywana współczynnikiem kierunkowym, a liczba b - wyrazem wolnym. Wykresem funkcji liniowej jest prosta
przecinająca oś OY w punkcie (0,b). Współczynnik kierunkowy jest tg kąta…
... zobacz całą notatkę






Komentarze użytkowników (0)