To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
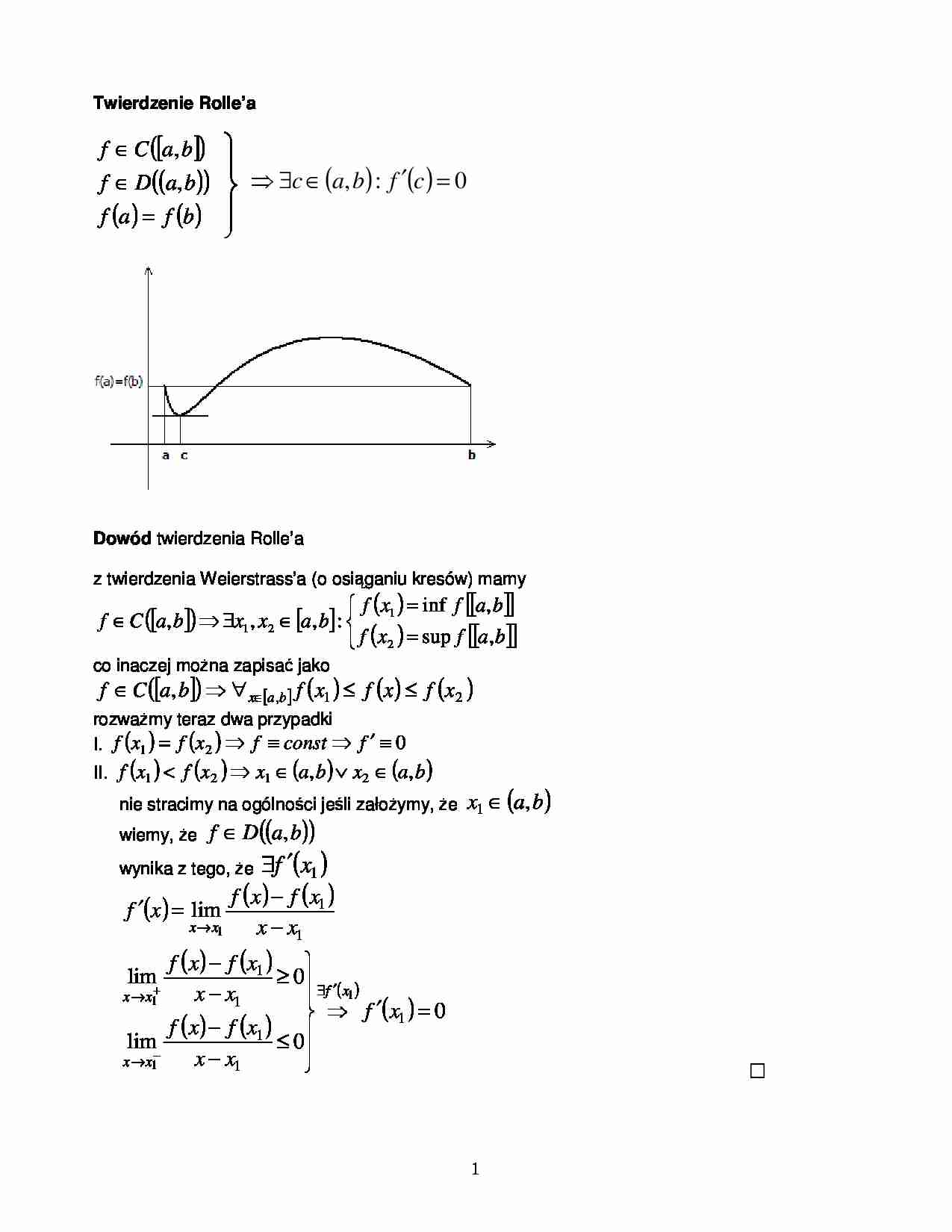


1 Twierdzenie Rolle’a [ ] ( ) ( ) ( ( ) ( ) b f a f b a D f b a C f = ∈ ∈ , , Dowód twierdzenia Rol e’a z twierdzenia Weierstrass’a (o osi ganiu kresów) mamy [ ] ( ) [ ] ( ) [ ] [ ( ) [ ] [ = = ∈ ∃ ∈ b a f x f b a f x f b a x x b a C f , sup , inf : , , , 2 1 2 1 co inaczej mo na zapisa jako [ ] ( ) [ ] ( ) ( ) ( ) 2 1 , , x f x f x f b a C f b a x ≤ ≤ ∀ ∈ ∈ rozwa my teraz dwa przypadki I. ( ) ( ) 0 2 1 ≡ ′ ≡ = f const f x f x f II. ( ) ( ) ( ) ( ) b a x b a x x f x f , , 2 1 2 1 ∈ ∨ ∈
(…)
… ])
f ∈ D((a, b ))
∃c ∈ (a, b ) : f ′(c ) =
f (b ) − f (a )
b−a
Prosta s to styczna do wykresu funkcji w punkcie styczno ci c, a prosta p ł czy ze sob punkty
(a, f (a )) oraz (b, f (b)) .
Wtedy obie proste wyra aj si nast puj cymi wzorami
f (b ) − f (a )
(x − a )
b−a
s : y = f (c ) + f ′(c )( x − c )
p : y = f (a ) +
Z tw. Lagrange’a wynika, e
s II p .
Dowód twierdzenia Lagrange’a
W celu ułatwienia…
... zobacz całą notatkę






Komentarze użytkowników (0)