To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
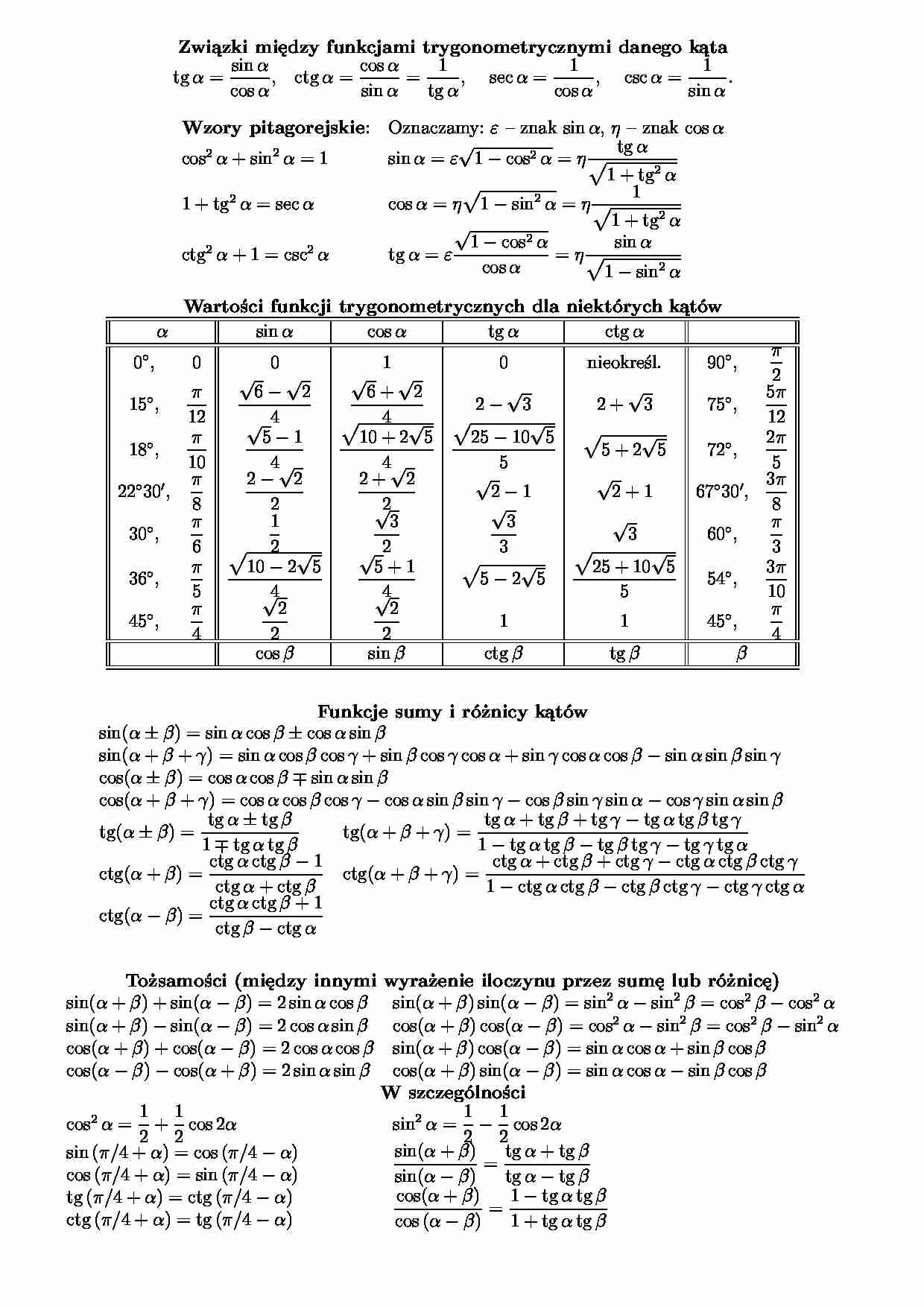

Związki między funkcjami trygonometrycznymi danego kąta
sin α
cos α
1
1
1
tg α =
, ctg α =
=
, sec α =
, csc α =
.
cos α
sin α
tg α
cos α
sin α
Wzory pitagorejskie:
cos2 α + sin2 α = 1
1 + tg2 α = sec α
ctg2 α + 1 = csc2 α
Oznaczamy: ε – znak sin α, η – znak cos α
√
tg α
sin α = ε 1 − cos2 α = η
1 + tg2 α
1
cos α = η 1 − sin2 α = η
1 + tg2 α
√
2α
1 − cos
sin α
tg α = ε
=η
cos α
1 − sin2 α
Wartości funkcji trygonometrycznych dla niektórych kątów
α
sin α
cos α
tg α
ctg α
0◦ ,
0
π
15 ,
12
π
18◦ ,
10
π
◦
22 30 ,
8
π
◦
30 ,
6
π
36◦ ,
5
π
◦
45 ,
4
◦
√
0
√
6− 2
√ 4
5−1
4√
2− 2
2
1
2 √
10 − 2 5
4
√
2
2
cos β
√
1
√
6+ 2
4 √
10 + 2 5
4√
2+ 2
2
√
3
√ 2
5+1
4
√
2
2
sin β
0
√
2− 3
√
25 − 10 5
5
√
2−1
√
3
3
√
5−2 5
nieokreśl.
√
2+ 3
√
5+2 5
√
2+1
√
3
√
25 + 10 5
5
1
1
ctg β
tg β
π
2
5π
◦
75 ,
12
2π
72◦ ,
5
3π
◦
67 30 ,
8
π
◦
60 ,
3
3π
54◦ ,
10
π
◦
45 ,
4
β
90◦ ,
Funkcje sumy i różnicy kątów
sin(α ± β) = sin α cos β ± cos α sin β
sin(α + β + γ) = sin α cos β cos γ + sin β cos γ cos α + sin γ cos α cos β − sin α sin β sin γ
cos(α ± β) = cos α cos β sin α sin β
cos(α + β + γ) = cos α cos β cos γ − cos α sin β sin γ − cos β sin γ sin α − cos γ sin α sin β
tg α + tg β + tg γ − tg α tg β tg γ
tg α ± tg β
tg(α + β + γ) =
tg(α ± β) =
1 tg α tg β
1 − tg α tg β − tg β tg γ − tg γ tg α
ctg α ctg β − 1
ctg α + ctg β + ctg γ − ctg α ctg β ctg γ
ctg(α + β) =
ctg(α + β + γ) =
ctg α + ctg β
1 − ctg α ctg β − ctg β ctg γ − ctg γ ctg α
ctg α ctg β + 1
ctg(α − β) =
ctg β − ctg α
Tożsamości (między innymi
sin(α + β) + sin(α − β) = 2 sin α cos β
sin(α + β) − sin(α − β) = 2 cos α sin β
cos(α + β) + cos(α − β) = 2 cos α cos β
cos(α − β) − cos(α + β) = 2 sin α sin β
1 1
+ cos 2α
2 2
sin (π/4 + α) = cos (π/4 − α)
cos (π/4 + α) = sin (π/4 − α)
tg (π/4 + α) = ctg (π/4 − α)
ctg (π/4 + α) = tg (π/4 − α)
cos2 α =
wyrażenie iloczynu przez sumę lub różnicę)
sin(α + β) sin(α − β) = sin2 α − sin2 β = cos2 β − cos2 α
cos(α + β) cos(α − β) = cos2 α − sin2 β = cos2 β − sin2 α
sin(α + β) cos(α − β) = sin α cos α + sin β cos β
cos(α + β) sin(α − β) = sin α cos α − sin β cos β
W szczególności
1 1
sin2 α = − cos 2α
2 2
sin(α + β)
tg α + tg β
=
sin(α − β)
tg α − tg β
cos(α + β)
1 − tg α tg β
=
cos (α − β)
1 + tg α tg β
Podwojenie kąta
sin 2α = 2 sin α cos α
cos 2α = 2 cos2 α − 1 = cos2 α − sin2 α = 1 − 2 sin2 α
2 tg α
sin 2α =
1 + tg2 α
1 − tg2 α
cos 2α =
1 + tg2 α
2 tg α
tg 2α =
1 − tg2 α
ctg2 α − 1
ctg 2α =
2 ctg2 α
Potrojenie kąta
sin 3α = sin α(3 cos2 α − sin2 α) = sin α(3 − 4 sin2 α)
cos 3α = cos α(cos2 α − 3 sin2 α) = cos α(4 cos2 α − 3)
3 − tg2 α
sin 3α = sin α
1 + tg2 α
1 − 3 tg2 α
cos 3α = cos α
1 + tg2 α
3 − tg2 α
tg 3α = tg α
1 − 3 tg2 α
ctg2 α − 3
ctg 3α = ctg α
3 ctg2 α − 1
Kąty połówkowe
1 + cos α
| cos α | =
2
2
1 − cos α
| sin α | =
2
2
1 − cos α
| tg α | =
2
1 + cos α
1 − cos α
sin α
=
tg α =
2
1 + cos α
sin α
Wyrażenie funkcji kąta α przez tg α
2
2 tg α
2
sin α =
1 + tg2 α
2
1 − tg2 α
2
cos α =
1 + tg2 α
2
2 tg α
2
tg α =
1 − tg2 α
2
1 − tg2 α
2
ctg α =
2 tg
... zobacz całą notatkę




Komentarze użytkowników (0)