To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
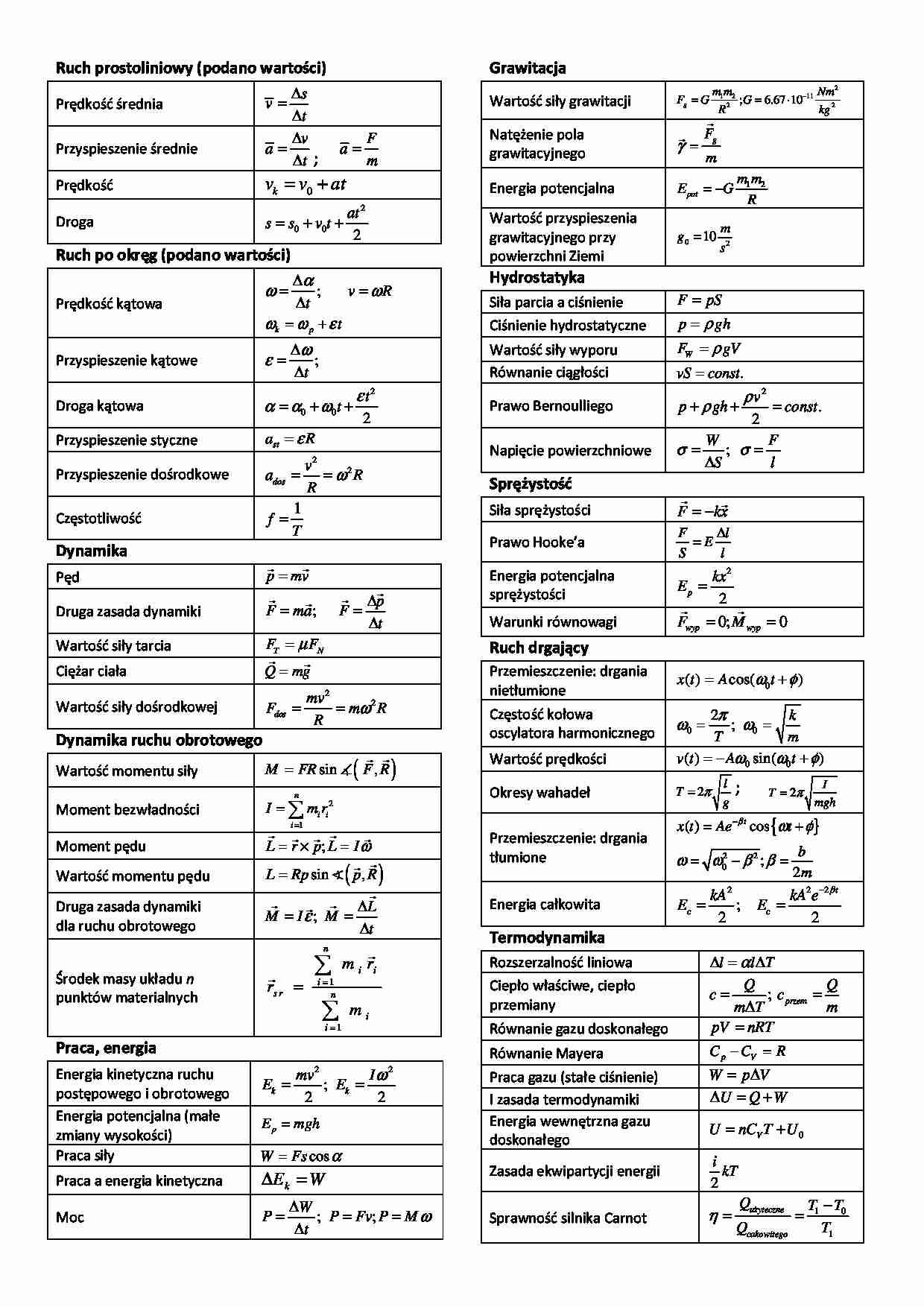

Ruch prostoliniowy (podano wartości) Grawitacja s
∆
2m mNm
1
2
1
− 1
Prędkość średnia v =
Wartość siły grawitacji F = G
;G = 6.67 ⋅
10g
2
2t
∆ Rkgv
∆F
Natężenie pola Fg
Przyspieszenie średnie a =a =
γ =
grawitacyjnego t
∆ ; m m
Prędkość v = v + at m mk
0
Energia potencjalna
1
2E
= G
−
potR
2at
Droga s = s + v t +
Wartość przyspieszenia
0
0m
2
grawitacyjnego przy g = 10
0
2Ruch po okręg (podano wartości) s
powierzchni Ziemi
αHydrostatyka
ω ∆
=
;v = ωR
Prędkość kątowa t
∆
Siła parcia a ciśnienie F = pS
ω = ω + εt
= ρ
kp
Ciśnienie hydrostatyczne pgh
ω
Wartość siły wyporu F = ρ gV
Przyspieszenie kątowe
ε ∆
=
;
W
∆t
Równanie ciągłości vS = const.
2
εt
2
ρv
Droga kątowa
α = α +ω t +
Prawo Bernoulliego p + ρ gh +
= const.
0
0
2
2
Przyspieszenie styczne a = ε R stWF
Napięcie powierzchniowe
σ =
; σ =
2vS
∆l
Przyspieszenie dośrodkowe
2a
=
= ω R dosRSprężystość
1
Siła sprężystości
= −
Częstotliwość Fkxf =
TFl
∆
Prawo Hooke’a
= E
Dynamika Sl
Pęd p = mv
Energia potencjalna
2kxE =pp
∆
sprężystości
2
Druga zasada dynamiki F = ma;F =
t
∆
Warunki równowagi F
= 0;M
= 0wypwyp
Wartość siły tarcia F = µ F TNRuch drgający
Ciężar ciała Q = mg
Przemieszczenie: drgania x(t) = Acos(ω t + φ)
2
nietłumione
0mv
Wartość siły dośrodkowej
2F
=
= mω Rdos
πR
Częstość kołowa
2k
ω =
; ω =
Dynamika ruchu obrotowego
oscylatora harmonicznego
0
0Tm
Wartość prędkości v(t) = − Aω sin(ω t + φ)
0
0
Wartość momentu siły M = FR sin ∡ ( F, R) l
= π
; I
= π
n
Okresy wahadeł T
2T
2gmgh
Moment bezwładności
2I = ∑ m r i i
−βi 1
=
( )tx t = Ae
cos{ωt +φ}
Przemieszczenie: drgania
Moment pędu L = r × p; L = Iω
tłumione b
2
2
ω = ω − β β =
;
0
Wartość momentu pędu L = Rp sin ∢( p, R)
2m
2
2
2
− βtkAkA e
Druga zasada dynamiki L
Energia całkowita E =
;E =
MIε
∆
= ; M =
c
2c
2
dla ruchu obrotowego t
∆Termodynamika n
∑ m r
Rozszerzalność liniowa
∆l = αl∆T ii
Środek masy układu n i = 1r
=
Ciepło właściwe, ciepło QQ
punktów materialnych s rnc =
; c
=
∑ m
przemiany m T
∆przemmii = 1
Równanie gazu doskonałego pV = nRT Praca, energia
Równanie Mayera C − C = R pV
Energia kinetyczna ruchu
2
2mvIω
Praca gazu (stałe ciśnienie) W = p V
∆ E =
; E =
postępowego i obrotowego k
2k
2
I zasada termodynamiki U
∆ = Q +W
Energia potencjalna (małe E = mgh
Energia wewnętrzna gazu
... zobacz całą notatkę




Komentarze użytkowników (0)