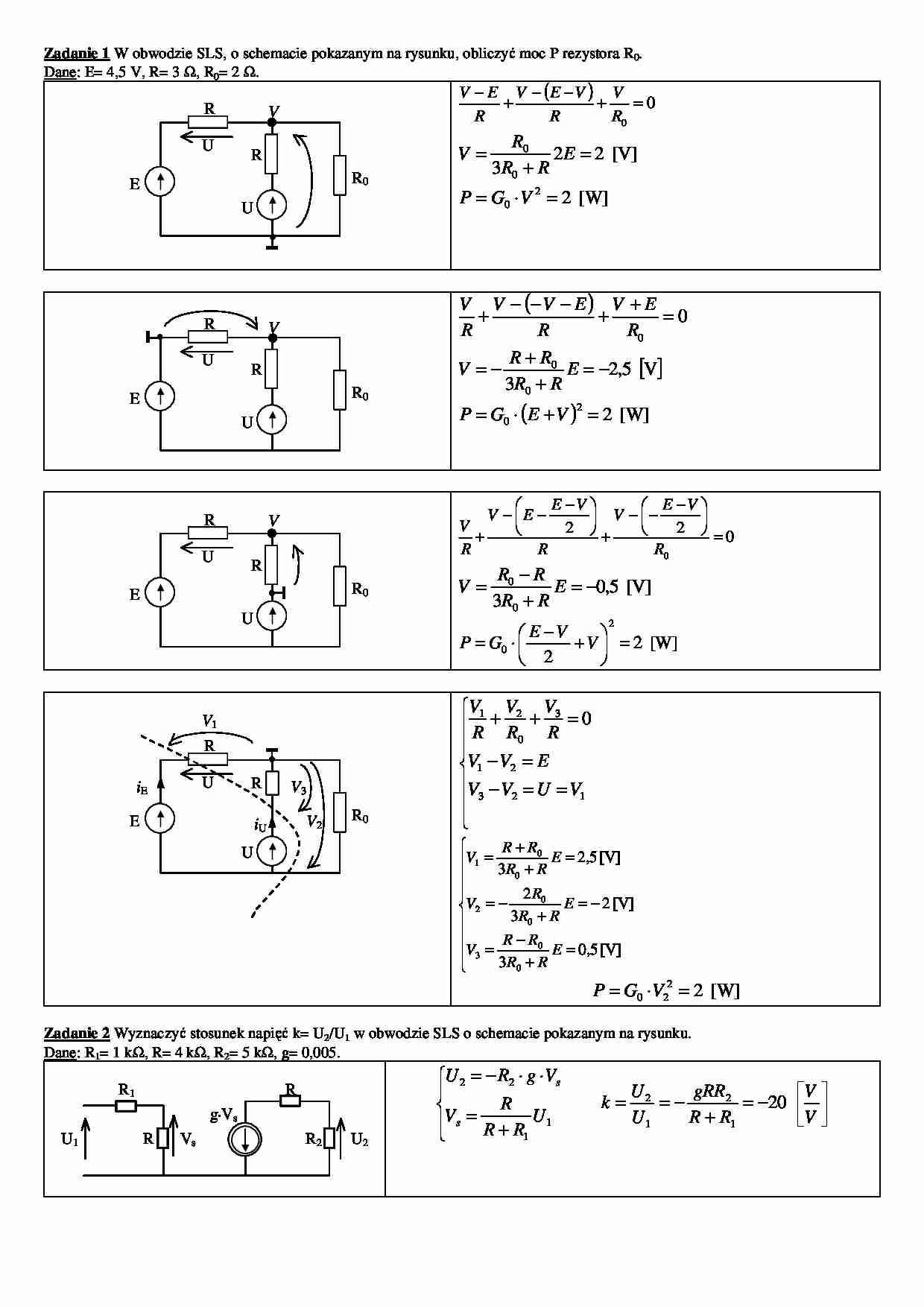
Zadanie 1 W obwodzie SLS, o schemacie pokazanym na rysunku, obliczyć moc P rezystora R0.
Dane: E= 4,5 V, R= 3 Ω, R0= 2 Ω.
R
U
V − E V − (E − V ) V
+
+
=0
R
R
R0
V
V=
R
R0
E
U
R
U
V
R
R0
E
R0
2 E = 2 [V]
3R0 + R
P = G0 ⋅ V 2 = 2 [W]
V V − (− V − E ) V + E
+
+
=0
R
R
R0
R + R0
V =−
E = −2,5 [V]
3R0 + R
P = G0 ⋅ (E + V ) = 2 [W]
2
U
R
U
V
V
+
R
R
R0
E
U
R
E
R0 − R
E = −0,5 [V]
3R0 + R
2
R
U
E −V
V − −
2
+
=0
R0
E −V
P = G0 ⋅
+ V = 2 [W]
2
V1
iE
V=
E −V
V −E −
2
R
V3
V2
iU
R0
V1 V2 V3
R + R + R = 0
0
V1 − V2 = E
V − V = U = V
1
3 2
R + R0
V1 = 3R + R E = 2,5 [V]
0
2 R0
E = − 2 [V]
V2 = −
3R0 + R
R − R0
E = 0,5 [V]
V3 =
3R0 + R
U
P = G0 ⋅ V22 = 2 [W]
Zadanie 2 Wyznaczyć stosunek napięć k= U2/U1 w obwodzie SLS o schemacie pokazanym na rysunku.
Dane: R1= 1 kΩ, R= 4 kΩ, R2= 5 kΩ, g= 0,005.
R
R1
g⋅Vs
U1
R
Vs
R2
U2
U 2 = − R2 ⋅ g ⋅ Vs
R
Vs = R + R U1
1
k=
U2
gRR2
=−
= −20
U1
R + R1
V
V
Zadanie 3 Oblicz moc elementu przyłączonego na prawo od zacisków A-B
1 kΩ
80 mA
I x = 80 ⋅ 10 −3 − 30 ⋅ 10 −3 − 2 I x
50
50
Ix =
mA
U x = 103 ⋅ I x =
V
3
3
50
50
5
P = U x ⋅ 2I x =
⋅ 2 ⋅ ⋅ 10 −3 = W = 0,556 W – pobiera energię
3
3
9
PPK:
A
2⋅Ix
30 mA
Ux
Ix
B
Zadanie 4 W obwodzie SLS, o schemacie pokazanym na rysunku, obliczyć moc P rezystora R0. Dane: E= 4,5 V, R= 3 Ω, R0= 2 Ω.
(zastosować Tw. „O źródle zastępczym”)
Prąd zwarcia
R
R
U
R
U
R0
E
R
Iz
E
U
U
Iz =
Napięcie jałowe
R
A I=0
U
Rezystancja zastępcza
Rw =
R
U0
E
U0 − E U0 − U
+
=0
R
R
Rw
R0
U 0 − E U 0 − (E − U 0 )
+
=0
R
R
U0 =
U0 1
= R = 1 [Ω ]
Iz 3
Schemat zastępczy
U
PPK dla w. A:
E U
E
+ = 2 = 3 [A]
R R
R
Iz
U0
2
E = 3 [V ]
3
2
R0
P = G0
R + R U 0 = 2 [W ]
w
0
R0
Rw
2
G0
P = R0
G + G I z = 2 [W ]
w
0
Zadanie 5 W obwodzie SLS o schemacie pokazanym na rysunku woltomierz pokazuje zero. Obliczyć wartość napięcia źródłowego E
oraz moce obu źródeł. Dane: J = 1 mA i R1 =R2 = 1 kΩ, R3 = 100 kΩ
I =0 A ⇒
V
R1
I
R3
J
U
R2
E
U=E
E =U = R⋅J =1 V
PE = E ⋅ I = 0 W
PJ = U J ⋅ J = (R1 + R2 ) ⋅ J 2 = 2 mW
Zadanie 6 W obwodzie SLS o schemacie pokazanym na rysunku obliczyć wartość rezystancji rezystora R0, przy której moc P0 tego
elementu będzie maksymalna oraz wyznaczyć wartość prądu I0 odpowiadający tej rezystancji. Dane: R = 0,25 Ω, E = 10 V
R
R
R
E
R
i
R
R
2⋅i
E
R0
V
i
R
U0
R
2⋅i
I0
R
R
E
i
R
V
Iz
R
2⋅i
E −U0
V − E V − U 0
R + R −2⋅ R = 0
U 0 + 2V = 3E
3U 0 − V = E
U 0 + U 0 − V + U 0 − E = 0
R
R
R
U
5
50
1
R0 = Rw = 0 =
U0 = E =
[V]
Ω
7
7
I z 14
Rw
I0
V −E V
E
+ − 2⋅ = 0
R
R
R
Iz =
V=
3
E = 15 [V]
2
U0
R0
I0 =
E V E 3E 5E
+ = +
=
= 100 A
R R R 2R 2R
1
I z = 50 [A]
2
Zadanie 7
1
SLS
40 Ω
E
1,2 = R + 60
w
E
3,0 =
Rw + 20
E
I =
Rw + 40
A
2
20 Ω
„1”
otwarty
zamknięty
otwarty
„2”
otwarty
otwarty
zamknięty
Amperomierz
1,2 A
3,0 A
???
E = 80 V
20
(…)
…
± (R1 + R2 + R )
R1
P +5
=
V
R − 15
P
− R2 E1
R
Zadanie 1 Obwód SLS złoŜony z idealnej cewki indukcyjnej o indukcyjności L = 66,2 mH i opornika R = 12 Ω jest zasilany
napięciem sinusoidalnie zmiennym o wartości skutecznej U = 120 Vsk i częstotliwości 50 Hz.
Obliczyć: wskazania przyrządów, moc pozorną i bierną, współczynnik mocy oraz narysować wykres wskazowy napięć i prądu.
R
I
A
W
U
L
ϕ
1
1…
… przyłączyć równolegle do dwójnika {R, L},
aby uzyskać współczynnik mocy czynnej: cosϕ1= 0,91.
A
*
* W
R=
I
C
R
U
IC
ϕ1 IRLC
ϕ
2
cos ϕ =
L
V
P
=
1200
= 10 Ω;
121
R 1
=
Z 2
ϕ=
Z =
U
I
220
= 20 Ω
11
π
[rad ] = 60 0
3
I RL ⋅ cos ϕ = I RLC ⋅ cos ϕ 1
I RLC = I RL ⋅
cos ϕ
cos ϕ1
cos ϕ
I C = I RL ⋅ sin ϕ − I RLC ⋅ sin ϕ1 = I RL ⋅ sin ϕ −
⋅ sin ϕ 1
cos ϕ1
cos ϕ
I C = I RL ⋅ 1 − cos 2 ϕ −
⋅ 1…
…| = |IR|
IR
A
R
XC
IC
I
U
Przed zamknięciem łącznika: |I| = |IC|
IC
I = 2 ⋅ IC
U
Zadanie 7. Układ złoŜony z kondensatora o pojemności C = 318 µF i opornika o oporności R = 5 Ω jest zasilany napięciem
sinusoidalnie zmiennym o wartości skutecznej U = 127 V i częstotliwości 50 Hz. Obliczyć: wskazania przyrządów, moc pozorną i
bierną, współczynnik mocy oraz narysować wykres wskazowy napięć i prądu.
P…
… zwarcia (napięcie wyjściowe u2 = 0):
iz = −α ⋅ i1 = −α ⋅
i1
α⋅i1
u1
= −0,1 ⋅ 10 −3 = − 0,1 mA
R1
Rezystancja wyjściowa:
k⋅u2
u1
u2 = −
i1
Rwy
R1
u1 − k ⋅ u2
R
1 24
41 3
iz
Rwy =
u2
R1 R2
=
= 25 kΩ
iz
R1 − R2 ⋅ α ⋅ k
Zadanie 19 Obliczyć wzmocnienie napięciowe Ku= u2/u1.
R2
R1
R1
–
–
∞
+
u1
u1
u
=− 2
R1
R2
R2
0V
u1
u2
Ku =
u2
+
u2
R
=− 2
u1
R1
Zadanie 20 Obliczyć moc czynną oporu R0.
R2
R1
u1
u1
u
=− 2
R1…
… na wartościach skutecznych.
2
2
127
16129
Q L = + X L I = +8 ⋅
2 =
Var
9
12
16129 16129 16129
Q = QL + QC =
−
=
Var
9
36
12
U
127
127
(1 − j ) A
I=
=
=
RL + j ( X L − X C ) 6 + j 6 12
127
I =
2 A
12
Zadanie 4 W obwodzie SLS w SUS o schemacie pokazanym na rysunku przyrządy wskazują: watomierz 1200 W, amperomierz 11
Ask, woltomierz 220 Vsk. Obliczyć reaktancję i moc bierną kondensatora, który naleŜy…
... zobacz całą notatkę





Komentarze użytkowników (0)