To tylko jedna z 10 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Bernat Jakub. Notatka składa się z 10 stron.
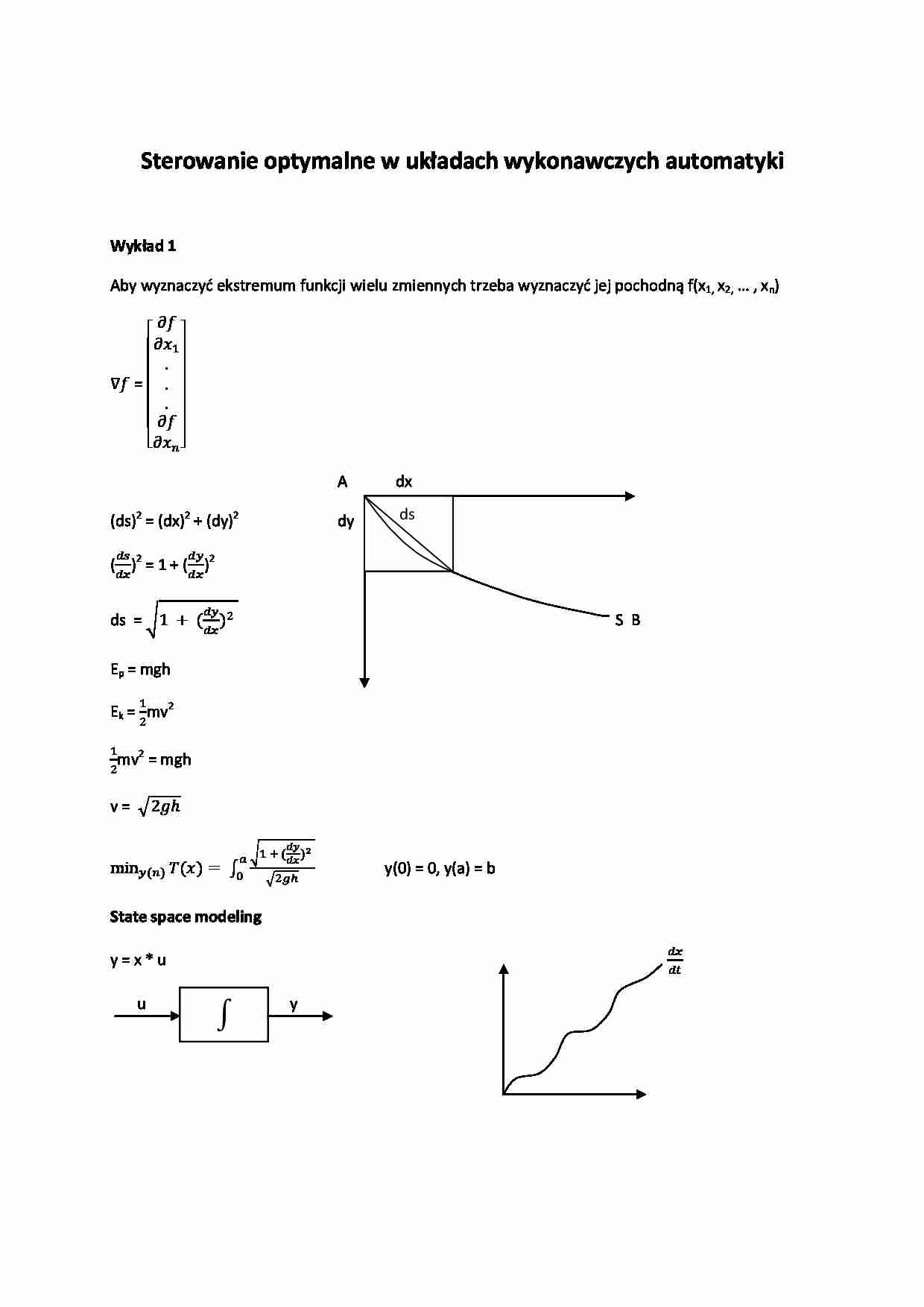
Sterowanie optymalne w układach wykonawczych automatyki Wykład 1 Aby wyznaczyd ekstremum funkcji wielu zmiennych trzeba wyznaczyd jej pochodną f(x1, x2, … , xn) = A dx (ds) 2 = (dx)2 + (dy)2 dy ( ) 2 = 1 + ( ) 2 ds = S B Ep = mgh Ek = mv 2 mv 2 = mgh v = y(0) = 0, y(a) = b State space modeling y = x * u u y ds x niesie ze sobą informację o tym co się dzieje aktualnie z układem i jak będzie się ona zachowywad w najbliższej przyszłości. Ponadto x powinien wyrażad zmiany energetyczne naszego systemu, zmienną stanu będzie taka wielkośd, która wyraża zmianę energii kinetycznej w naszym systemie. = Ax + Bu Y = Cx + Du Sterowanie optymalne Polega na wyborze takiego sterowania u ze zbioru sterowao dopuszczalnych, które jest w stanie przeprowadzid system dynamiczny z pewnego x(t0) w czasie t0 do pewnego stanu koocowego x(T) w ustalonym czasie T tak, aby zapewnid minimalizację bądź maksymalizację pewnej funkcji celu. Wykład 2 Sterowanie – zadaniem sterowania optymalnego jest znalezienie takiej funkcji sterowania u*, która należy do klasy sterowao dopuszczalnych i przeprowadza układ o równaniu stanu sterowania i czasu według trajektorii optymalnej x’. x’ – ekstrema lizuje określoną funkcję celu J = h(x(T),T) + Rozpatrzymy system opisany równaniami stanu w których kryje się dynamika tego systemu i przyjmijmy, że funkcja F jest klasy C 2( f C2 ) (istnieje 2 pochodna) w której też występują zmienne stanu pochodnej zmiennej x. W celu optymalizacji wykorzystamy oraz . Mogą wystąpid przypadki szczególne, w których stan nie występuje w sposób niejawny. Warunkiem koniecznym ekstremalizacji wskaźnika J = gdzie funkcja F C 2 o punkcie początkowym xt0 = A i koocowym x(T) = B jest spełnieniem równania Eulera-Lagrange’a
(…)
… (*) przy
czym w ogólnym przypadku równanie to może byd równaniem liniowym niestacjonarnym zależnym
liniowo od macierzy A.
Rozwiązanie tego równania znajduje się poprzez wykorzystanie metody Newtona numerycznego
rozwiązania równao nieliniowych.
Wykład 7
Zasada maksimum Pontiagina
Dotychczas rozpatrywaliśmy funkcję sterowania optymalnego jako funkcję ciągłą. W niektórych
jednak przypadkach może okazad…
…) =
=Q,
Q=const
x(0), x(T) – dane, ustalone
Musimy zamienid ograniczenia całkowe na ograniczenia różniczkowe:
z’ = q
z=
z(0) = 0 , z(T) = Q
Ja(x) =
=0
T
=0
Wykład 4
Sterowanie optymalne:
Niech obiekt sterowania będzie dany równaniem
,
, ponadto
przyjmijmy, że początek trajektorii stanu jest podany x(0), a koniec trajektorii x(T) = free. Będziemy
poszukiwad takiego sterowania optymalnego…
… BTp
p’ = -
= -Qx – ATp
p=K*x
p’= K’x + Kx’ = -Qx - ATKx
K’x + K(Ax+Bu*) + Qx + ATKx = 0
K’x + KAx + ATKx + KBu* + Qx = 0
K’x + KAx + ATKx - KBR-1 BTKx + Qx = 0
K’ + KA + ATK - KBR-1 BTK + Q = 0 Równanie Riccatiego
Najczęściej rozwiązuje się je numerycznie stosując np. dyskretyzację Eulerowską taką, że
K’ =
= -KiA - ATKi + KiBR-1BTKi – Q
Ki+1 = Ki +
( -KiA - ATKi + KiBR-1BTKi – Q )
T 0 Ki+1 = Ki T…
… z równaniem dynamiki obiektu przeprowadzamy ze stanu
początkowego x(0) do koocowego x(T). Istnieje jeszcze rodzaj rozwiązania LQR z tzw. Nieskooczonym
horyzontem czasowym, w którym czas referencyjny jest asymptotą stanu osiągniętego przez obiekt.
Wykład 6
Sterowanie LQR z nieskooczonym horyzontem czasowym
J(n) =
,
p.o. x’ = Ax+Bu
+ pT(Ax+Bu)
H= (
= 0 Ru + BTp = 0
u = -R-1BTp = -R-1BTRx
p’=K’x+Kx’
K=const…
... zobacz całą notatkę






Komentarze użytkowników (0)