To tylko jedna z 9 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
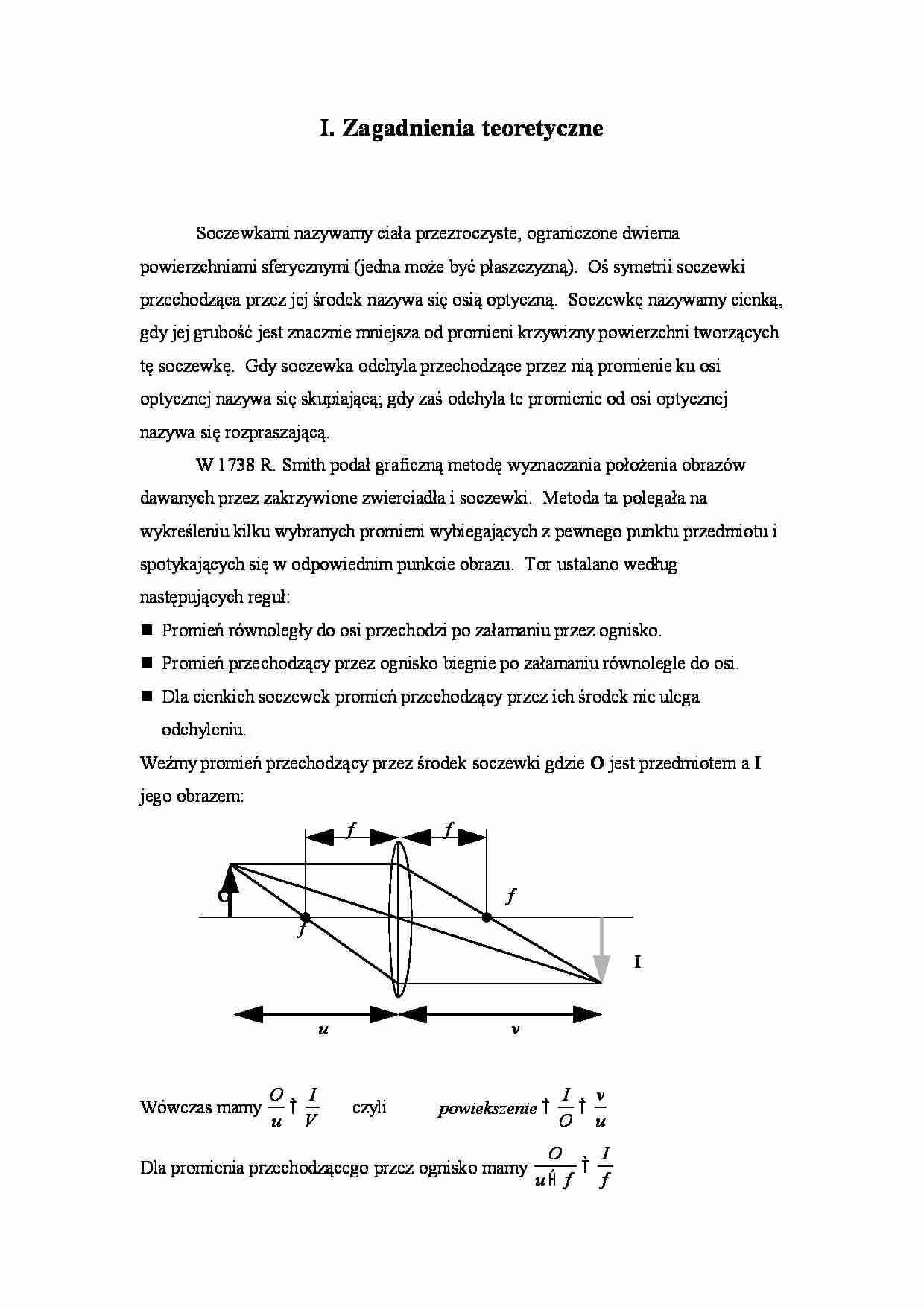


I. Zagadnienia teoretyczne Soczewkami nazywamy ciała przezroczyste, ograniczone dwiema powierzchniami sferycznymi (jedna może być płaszczyzną). Oś symetrii soczewki przechodząca przez jej środek nazywa się osią optyczną. Soczewkę nazywamy cienką, gdy jej grubość jest znacznie mniejsza od promieni krzywizny powierzchni tworzących tę soczewkę. Gdy soczewka odchyla przechodzące przez nią promienie ku osi optycznej nazywa się skupiającą; gdy zaś odchyla te promienie od osi optycznej nazywa się rozpraszającą. W 1738 R. Smith podał graficzną metodę wyznaczania położenia obrazów dawanych przez zakrzywione zwierciadła i soczewki. Metoda ta polegała na wykreśleniu kilku wybranych promieni wybiegających z pewnego punktu przedmiotu i spotykających się w odpowiednim punkcie obrazu. Tor ustalano według następujących reguł: n Promień równoległy do osi przechodzi po załamaniu przez ognisko. n Promień przechodzący przez ognisko biegnie po załamaniu równolegle do osi. n Dla cienkich soczewek promień przechodzący przez ich środek nie ulega odchyleniu. Weźmy promień przechodzący przez środek soczewki gdzie O jest przedmiotem a I jego obrazem: f f O f f I u v Wówczas mamy O u I V czyli powiekszenie I O v u Dla promienia przechodzącego przez ognisko mamy O u f I f Eliminując O oraz I za pomocą wzoru na powiększenie otrzymujemy 1 u f v uf a stąd 1 1 1 f v u Przekształcając nieco to wyrażenie, otrzymamy wzór na ogniskową soczewki: f uv u v Korzystając z definicji i wzorów na załamanie światła można otrzymać wzór: 1 1 1 1 1 1 1 2 f u v R R
(…)
… było doświadczalne zmierzenie długości
ogniskowej trzech różnych soczewek (dwóch skupiających i jednej rozpraszającej) za
pomocą ławy optycznej, korzystając z trzech metod obliczeń: liniowej, Bessela, i z
wielkości powiększonego obrazu. W tym celu odpowiednio pomierzono pozycje
soczewek przy kilku wybranych odległościach ekranu od źródła światła dla
powiększonego i pomniejszonego obrazu tworzonego na ekranie…
…. We wszystkich
przypadkach, w celu uzyskania ogniskowej soczewki rozpraszającej, połączono ją z
jedną z soczewek skupiających a następnie w obliczeniach skorzystano ze wzoru na
ogniskową kombinacji soczewek, podanego wcześniej.
III Opracowanie wyników pomiarów
a) Metoda liniowa:
W celu lepszego przybliżenia odległości środka soczewek od źródła światła,
zmierzono jej odległość jak i jej odległość po odwróceniu o 180 stopni, przy stałej
odległości ekranu od źródła światła. Wówczas można było już sporządzić poniższą
tabelę, gdzie wartość ogniskowej została automatycznie wyliczona wg. następującego
algorytmu opartego na wzorze f
uv
, gdzie u jest średnią odległością soczewki
u v
od przedmiotu a v odległością ekranu od soczewki (odl. ekranu odjąć poz. soczewki):
Wszystkie w artości w centymetrach
obraz pomniejszony
odl. ekranu…
…: promienie różnobarwne załamują się różnie w zależności
od długości fali światła i współczynnika załamania. Swiatło fioletowe załamuje
się bardziej od np. czerwonego. Można zmniejszyć efekty abberacji
chromatycznej stosując układ soczewek z różnego szkła (o innym współczynniku
załamania).
n Astygmatyzm: specyficzne odchylenie od homocentryczności z powodu asymetrii
powierzchni ograniczającej soczewkę od osi…
… załamania światła, a R1 i R2 są promieniami krzywizny
obu powierzchni soczewki. Wzór ten jest wyprowadzony jednak jedynie dla promieni
bardzo bliskich osi i bardzo cienkich soczewek.
Dla soczewek wypukłych f (odległość ogniskowa soczewki) jest dodatnia, dla
wklęsłych ujemna. Ten wzór, jak i wzór na powiększenie tłumaczą rodzaje obrazów
dawanych przez soczewki wklęsłe i wypukłe. Gdy przedmiot znajduje…
…(2)=12.40 cm; f(3+2)=17.12 cm. Analogicznie otrzymujemy wartość ogniskowej
soczewki rozpraszającej 3: f(3)=-44.98 cm.
IV Opracowanie błędów
Obliczamy błędy metodą różniczki zupełnej dla trzech metod wyznaczania
ogniskowej:
a)
metoda liniowa ze wzoru f
uv
:
u v
v ( u v ) uv
u(u v ) uv
f
f
u
v
u
v
2
(u v )
(u v ) 2
u
v
b)
metoda Bessela dla wzoru f
1 l 2 d 2
:
4…
... zobacz całą notatkę






Komentarze użytkowników (0)