To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


RUCH HARMONICZNY 1. Równanie ruchu harmonicznego Jako przykład rozpatrzmy ruch ciała o masie m zawieszonego na sprężynie (czerwona kulka). Siła przywracająca ciało do położenia równowagi zależna jest od wielkości odchylenia i jeśli odkształcenia są doskonale sprężyste, wyrażona jest przez znane nam już prawo Hooke'a (patrz wzór (3.28) oraz animacja powyżej.) (6.1) W zależności tej F jest siłą, x - odchyleniem, czyli aktualnym położeniem ciała określonym względem położenia równowagi; k jest współczynnikiem proporcjonalności charakteryzującym własności sprężyny. Jeżeli współczynnik ten nie zmienia się w czasie ruchu, to wartość siły jest wprost proporcjonalna do wielkości odchylenia od położenia równowagi. Ruch odbywający się pod wpływem takiej siły nazywamy ruchem harmonicznym, a siły o tej własności nazywamy siłami harmonicznymi. Proporcjonalność siły do odchylenia jest najbardziej charakterystyczną własnością, wspólną dla wszystkich sił harmonicznych, mimo że siły te nie ograniczają się wyłącznie do sił sprężystości. Znak minus oznacza, że kierunek siły jest przeciwny do kierunku odchylenia. 2.Równanie Newtona dla siły harmonicznej Korzystając z drugiego prawa dynamiki możemy równanie ruchu ciała o masie m pod działaniem siły (6.1) zapisać następująco:
(6.2) Przepiszemy to równanie w postaci (6.2a) gdzie wprowadziliśmy wielkość w zdefiniowaną jako (6.3) Równanie (6.2a) jest równaniem różniczkowym drugiego rzędu. Niewiadomą w tym równaniu jest odchylenie od położenia równowagi x, a ściślej mówiąc, zależność tego odchylenia od czasu t. Poszukujemy więc takiej funkcji x=f(t), której druga pochodna d2x/dt2 równa jest jej samej wziętej ze znakiem minus i pomnożonej przez pewną stałą, którą oznaczyliśmy przez w2.
Jaka funkcja ma taką właściwość? Oczywiście - funkcje, sinus i cosinus. Nietrudno sprawdzić, że podany wyżej warunek zostanie zachowany także jeśli funkcje te pomnożymy przez stały czynnik, a do argumentu dodamy dowolną stałą. 3.Postać rozwiazania Sprawdźmy więc, czy podany wyżej warunek będzie spełniony zakładając, że rozwiązanie ma postać: (6.4) gdzie A oraz j, to wartości stałe, nie zmieniające się w czasie.
(…)
… nie zależy ani od x, ani od u i jest w każdej chwili (a więc i w każdym punkcie) taka sama, wprost proporcjonalna do kwadratu amplitudy. Wynik ten nie dziwi nas; jest prostą konsekwencją zasady zachowania energii. Odchylenie ciała od położenia równowagi, to dostarczenie mu energii potencjalnej. Jeżeli potem nie ingerujemy w ruch ciała, to uzyskiwana w czasie ruchu do położenia równowagi energia kinetyczna…
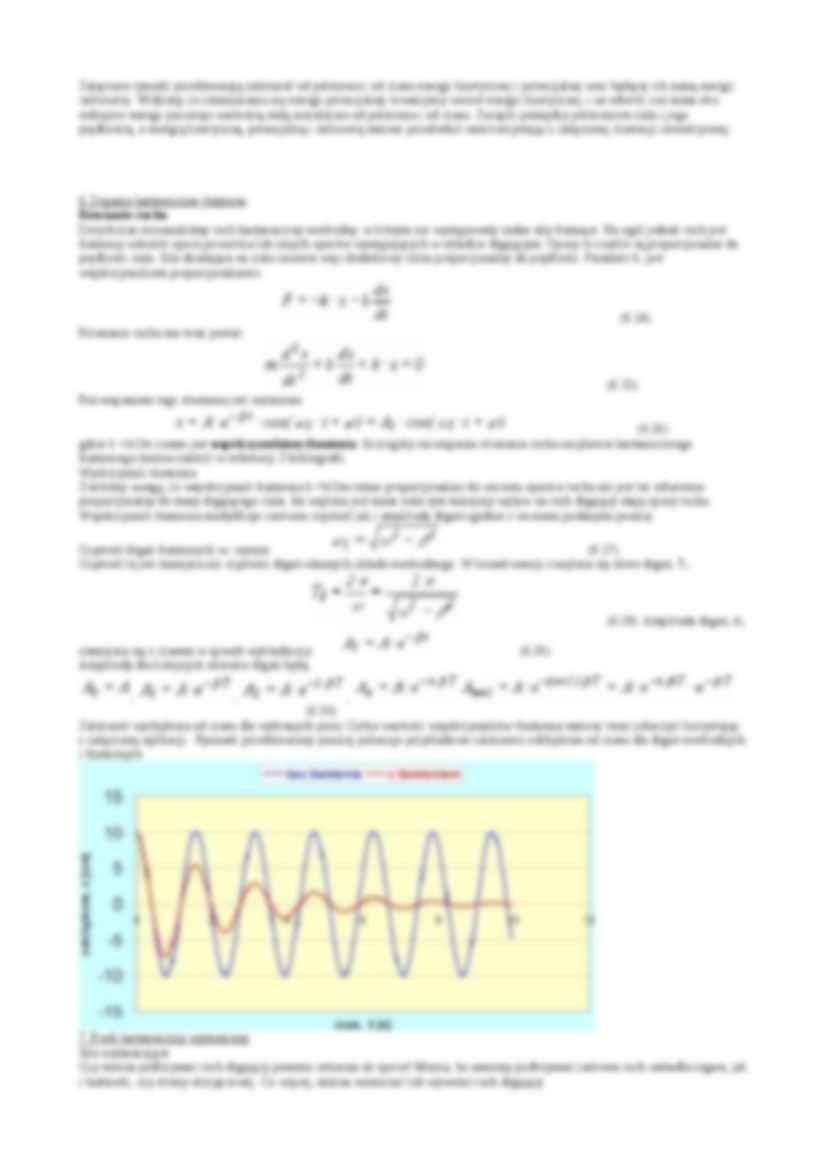
… na ruch drgający mają opory ruchu. Współczynnik tłumienia modyfikuje zarówno częstość jak i amplitudę drgań zgodnie z wzorami podanymi poniżej. Częstość drgań tłumionych w1 wynosi: (6.27) Częstość ta jest mniejsza niż częstości drgań własnych układu swobodnego. W konsekwencji zwiększa się okres drgań, T1. (6.28) Amplituda drgań, A1 zmniejsza się z czasem w sposób wykładniczy: (6.29) Amplitudy…
... zobacz całą notatkę






Komentarze użytkowników (0)