To tylko jedna z 20 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
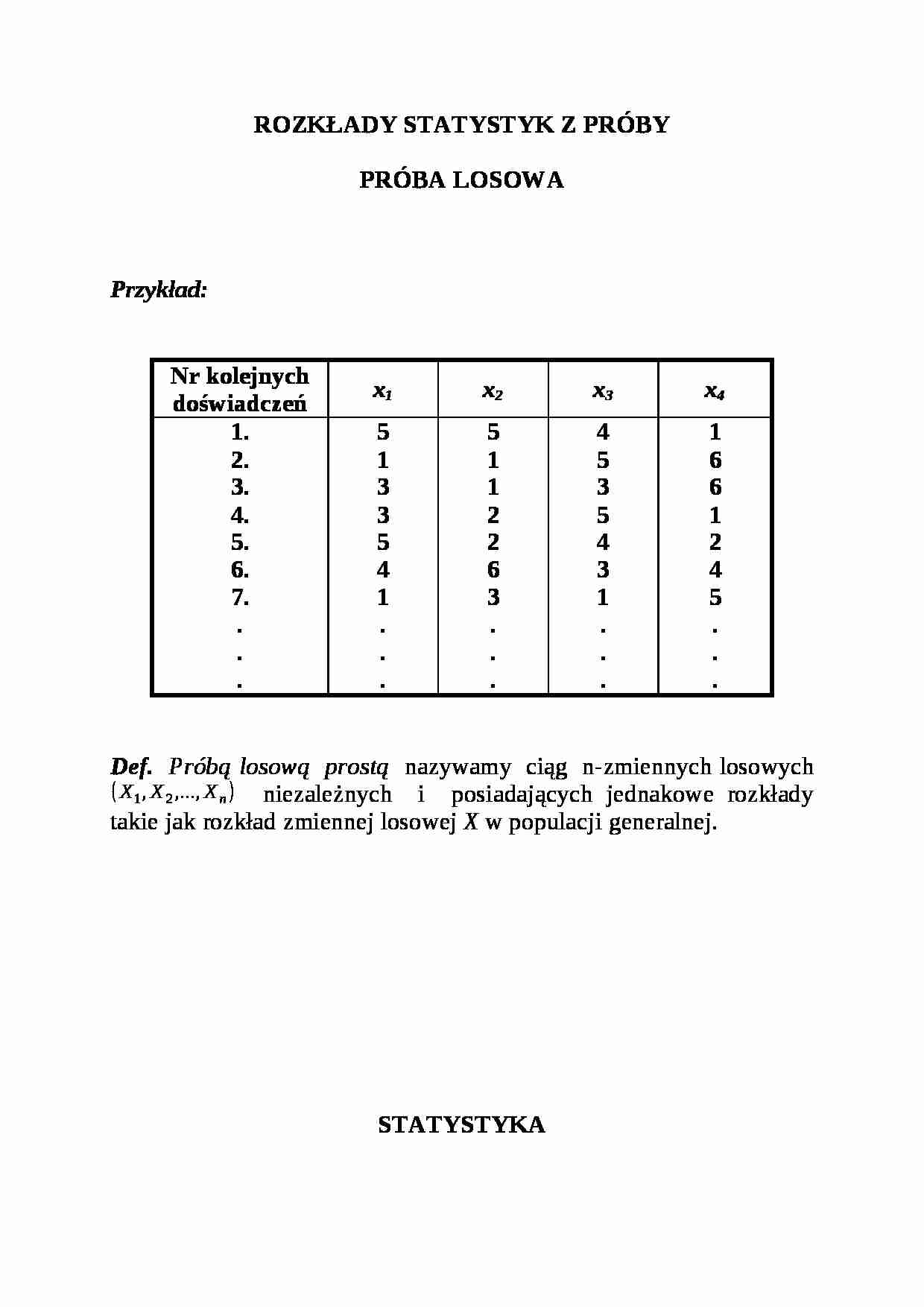


ROZKŁADY STATYSTYK Z PRÓBY PRÓBA LOSOWA Przykład: Nr kolejnych doświadczeń x 1 x 2 x 3 x 4 1. 2. 3. 4. 5. 6. 7. . . . 5 1 3 3 5 4 1 . . . 5 1 1 2 2 6 3 . . . 4 5 3 5 4 3 1 . . . 1 6 6 1 2 4 5 . . . Def. Próbą losową prostą nazywamy ciąg n-zmiennych losowych niezależnych i posiadających jednakowe rozkłady takie jak rozkład zmiennej losowej X w populacji generalnej.
STATYSTYKA Def. Statystyką (z próby) nazywamy zmienną losową Z n będącą funkcją zmiennych losowych stanowiących próbę losową.
Przykład: - statystyka jako funkcja zmiennych losowych sama jest zmienną losową, która posiada pewien rozkład
- rozkład statystyki nazywa się rozkładem z próby
ROZKŁAD ŚREDNIEJ ARYTMETYCZNEJ Z PRÓBY DLA POPULACJI NORMALNEJ ZE ZNANYM ODCHYLENIEM STANDARDOWYM Założenia - cecha X ma w populacji rozkład normalny ze średnią m i odchyleniem standardowym , - z populacji pobieramy n-elementową próbę losową prostą (X 1 , X 2 ,...,X n ). Średnia arytmetyczna z próby posiada przy powyższych założeniach rozkład normalny ze średnią i odchyleniem standardowym :
Dowód: ROZKŁAD ŚREDNIEJ ARYTMETYCZNEJ Z PRÓBY DLA POPULACJI NORMALNEJ Z NIEZNANYM ODCHYLENIEM STANDARDOWYM
(…)
… lub funkcji gęstości.
Integralne twierdzenia graniczne - twierdzenia mówiące o zbieżności ciągu dystrybuant.
TWIERDZENIE DE MOIVRE`A - LAPLACE`A
Twierdzenie (integralne)
Niech {Xn} będzie ciągiem zmiennych losowych o rozkładzie dwumianowym z parametrami n i 0<p<1 oraz niech {Un} będzie ciągiem wystandaryzowanych zmiennych :
Wtedy dla ciągu dystrybuant zmiennych losowych Un zachodzi:
dla każdej wartości u.
Wniosek
Ciąg dystrybuant zmiennych losowych {Xn} o rozkładzie dwumianowym z parametrami n i p (niestandaryzowanych) jest zbieżny do rozkładu normalnego .
Wniosek
Jeśli rozpatrzymy ciąg zmiennych , to z twierdzenia de Moivre'a-Laplace'a wynika, że zmienna ta ma asymptotyczny rozkład normalny .
CENTRALNE TWIERDZENIE GRANICZNE LINDEBERGA-LEVY`EGO
Założenia
Rozpatrujemy ciąg niezależnych zmiennych losowych…
... zobacz całą notatkę






Komentarze użytkowników (0)