To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

ROZKŁAD POISSONA
Dyskretny rozkład prawdopodobieństwa stosowany przy wielokrotnym powtarzaniu doświadczenia w przypadku, gdy prawdopodobieństwo oczekiwanego zdarzenia jest bardzo małe. Ma zastosowanie dla n ≥ 30 i p ≤ 0,2.
Funkcja gęstości prawdopodobieństwa wyraża się wzorem:
Zbiór wartości funkcji: Parametry:
λ - jest dodatnią liczbą rzeczywistą, równą oczekiwanej liczbie zdarzeń w danym przedziale. k - liczba wystąpień zdarzenia.
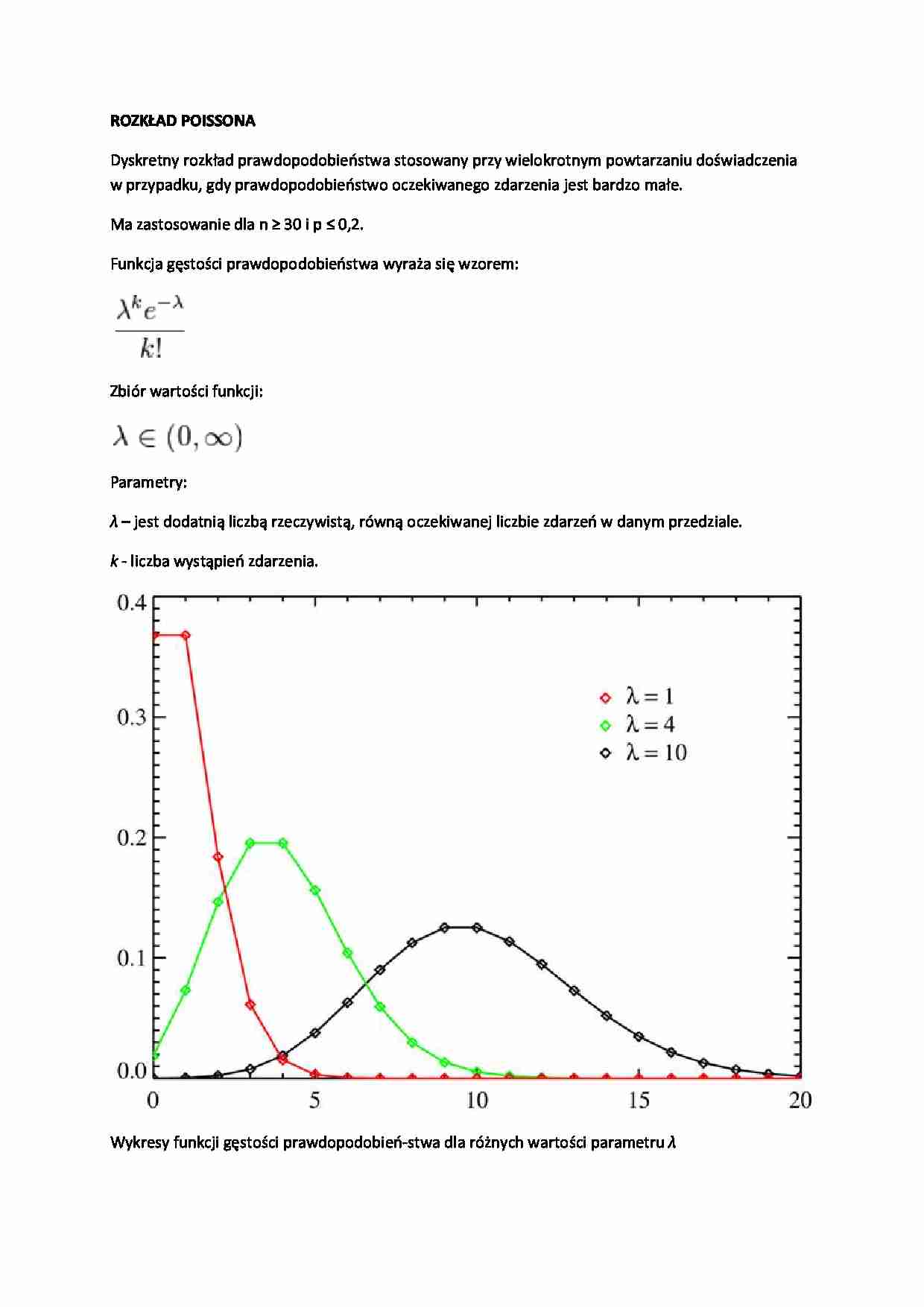
Wykresy funkcji gęstości prawdopodobień-stwa dla różnych wartości parametru λ ZASTOSOWANIE
Główne zastosowania:
Stosowany w układach mechanicznych, gdzie poziom wytrzymałości jest znacznie wyższy od poziomu występujących losowych naprężeń,
Opisanie liczby awarii występujących w procesie produkcyjnym,
Liczbę zabitych przez kopnięcie konia każdego roku w korpusie kawalerii w Prusach. (Władysław Józefowicz Bortkiewicz (1868-1931). Przykład:
W pudełku jest 400 żarówek. Jakie jest prawdopodobieństwo, że wśród nich jest 5 żarówek wadliwych, jeśli wadliwość produkcji takich żarówek wynosi 0,5%?
Jaka jest najbardziej prawdopodobna liczba uszkodzonych żarówek w tym pudełku?
Zastosowanie przybliżenia Poissona: Z tablicy rozkładu Poissona: Również z tablicy Poissona można odczytać, że najbardziej prawdopodobna liczba uszkodzonych żarówek w pudełku wynosi 1 lub 2 (dla obu tych liczb prawdopodobieństwo jest równe 0,2707).
... zobacz całą notatkę




Komentarze użytkowników (0)