To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
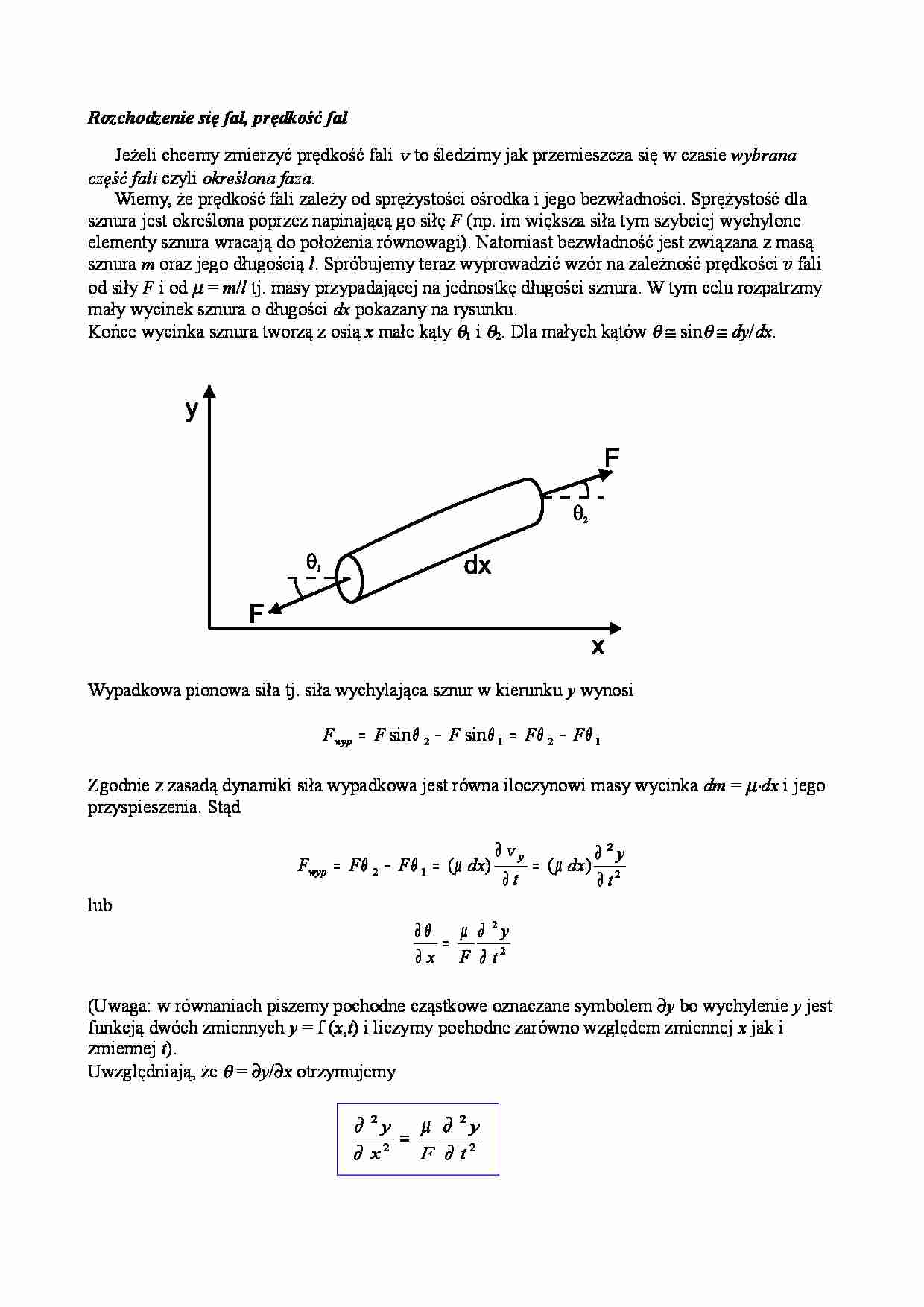

Rozchodzenie się fal, prędkość fal Jeżeli chcemy zmierzyć prędkość fali v to śledzimy jak przemieszcza się w czasie wybrana część fali czyli określona faza . Wiemy, że prędkość fali zależy od sprężystości ośrodka i jego bezwładności. Sprężystość dla sznura jest określona poprzez napinającą go siłę F (np. im większa siła tym szybciej wychylone elementy sznura wracają do położenia równowagi). Natomiast bezwładność jest związana z masą sznura m oraz jego długością l . Spróbujemy teraz wyprowadzić wzór na zależność prędkości v fali od siły F i od µ = m / l tj. masy przypadającej na jednostkę długości sznura. W tym celu rozpatrzmy mały wycinek sznura o długości dx pokazany na rysunku. Końce wycinka sznura tworzą z osią x małe kąty θ1 i θ2. Dla małych kątów θ ≅ sinθ ≅ dy / dx . Wypadkowa pionowa siła tj. siła wychylająca sznur w kierunku y wynosi 1 2 1 2 θ θ θ θ F F F F F wyp − = − = sin sin Zgodnie z zasadą dynamiki siła wypadkowa jest równa iloczynowi masy wycinka dm = µ⋅ dx i jego przyspieszenia. Stąd 2 1 2 ) ( ) ( t y dx t dx F F F y wyp ∂ ∂ = ∂ ∂ = − = 2 µ µ θ θ v lub 2 2 t y F x ∂ ∂ µ θ = ∂ ∂ (Uwaga: w równaniach piszemy pochodne cząstkowe oznaczane symbolem ∂ y bo wychylenie y jest funkcją dwóch zmiennych y = f ( x , t ) i liczymy pochodne zarówno względem zmiennej x jak i zmiennej t ). Uwzględniają, że θ = ∂ y /∂ x otrzymujemy 2 2 2 2 t y F x y ∂ ∂ µ ∂ ∂ = Jest to równanie falowe dla sznura (struny). Podstawmy teraz do tego równania odpowiednie pochodne funkcji ) sin( ) , f( t x k A t x y ω − = = ) sin( t x k A t y ω ω ∂ ∂ − − = 2 2 2 oraz ) sin( t x k Ak x y ω ∂ ∂ − − = 2 2 2 W wyniku podstawienia otrzymujemy 2 2 ω µ F k = skąd możemy obliczyć prędkość fali µ ω F k = = v Zwróćmy uwagę, że sinusoidalna fala może być przenoszona wzdłuż struny z prędkością niezależną od amplitudy i częstotliwości. Jeżeli teraz przepiszemy równanie struny w postaci 2 2 2 2 2 1 t y x y ∂ ∂ ∂ ∂ v = to otrzymamy równanie falowe , które stosuje się do wszystkich rodzajów rozchodzących się fal, takich jak fale dźwiękowe czy elektromagnetyczne. Document Outline Rozchodzenie się fal, prędkość fal
... zobacz całą notatkę




Komentarze użytkowników (0)