To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
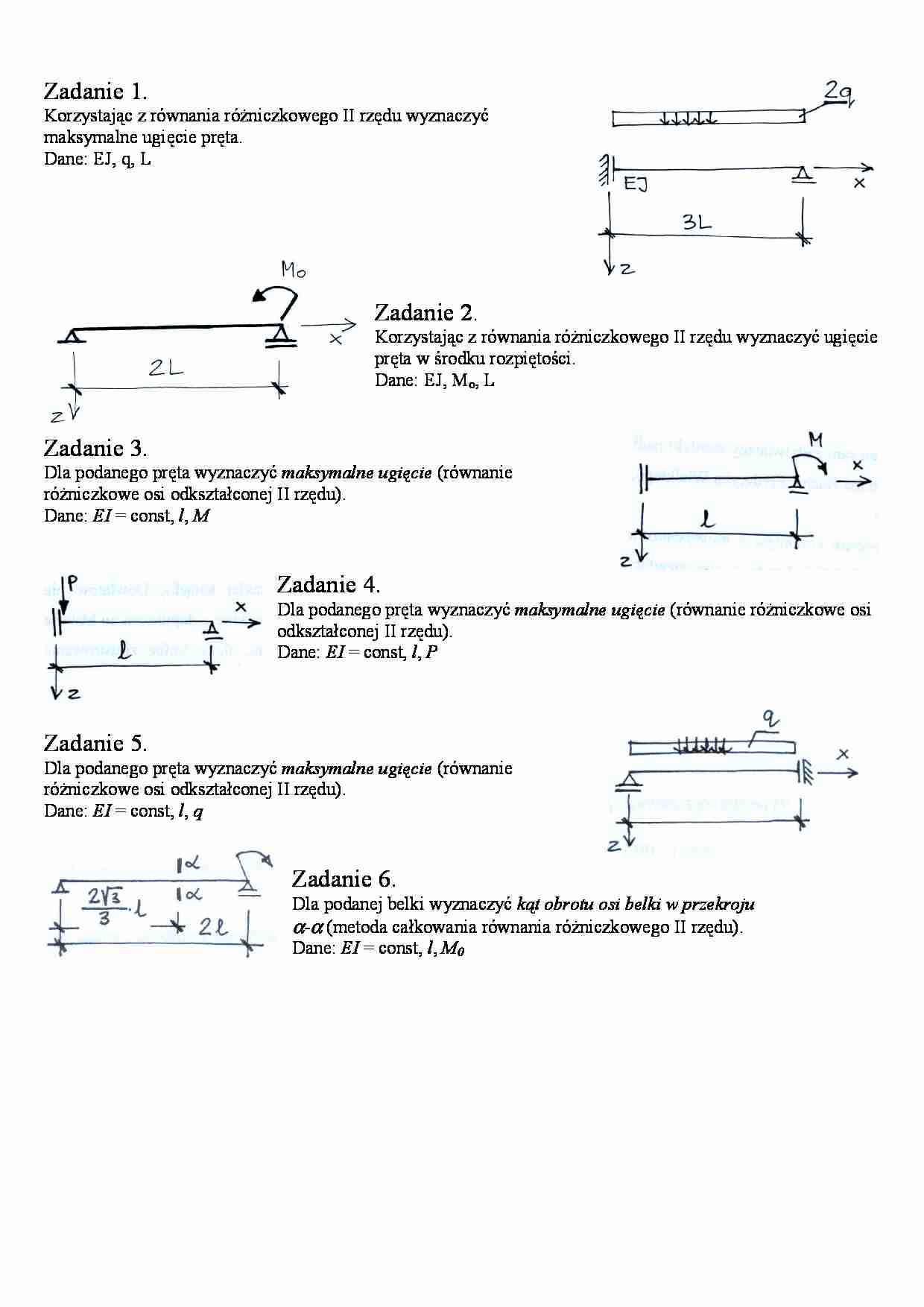
Zadanie 1.
Korzystając z równania różniczkowego II rzędu wyznaczyć
maksymalne ugięcie pręta.
Dane: EJ, q, L
Zadanie 2.
Korzystając z równania różniczkowego II rzędu wyznaczyć ugięcie
pręta w środku rozpiętości.
Dane: EJ, Mo, L
Zadanie 3.
Dla podanego pręta wyznaczyć maksymalne ugięcie (równanie
różniczkowe osi odkształconej II rzędu).
Dane: EI = const, l, M
Zadanie 4.
Dla podanego pręta wyznaczyć maksymalne ugięcie (równanie różniczkowe osi
odkształconej II rzędu).
Dane: EI = const, l, P
Zadanie 5.
Dla podanego pręta wyznaczyć maksymalne ugięcie (równanie
różniczkowe osi odkształconej II rzędu).
Dane: EI = const, l, q
Zadanie 6.
Dla podanej belki wyznaczyć kąt obrotu osi belki w przekroju
α-α (metoda całkowania równania różniczkowego II rzędu).
Dane: EI = const, l, M0
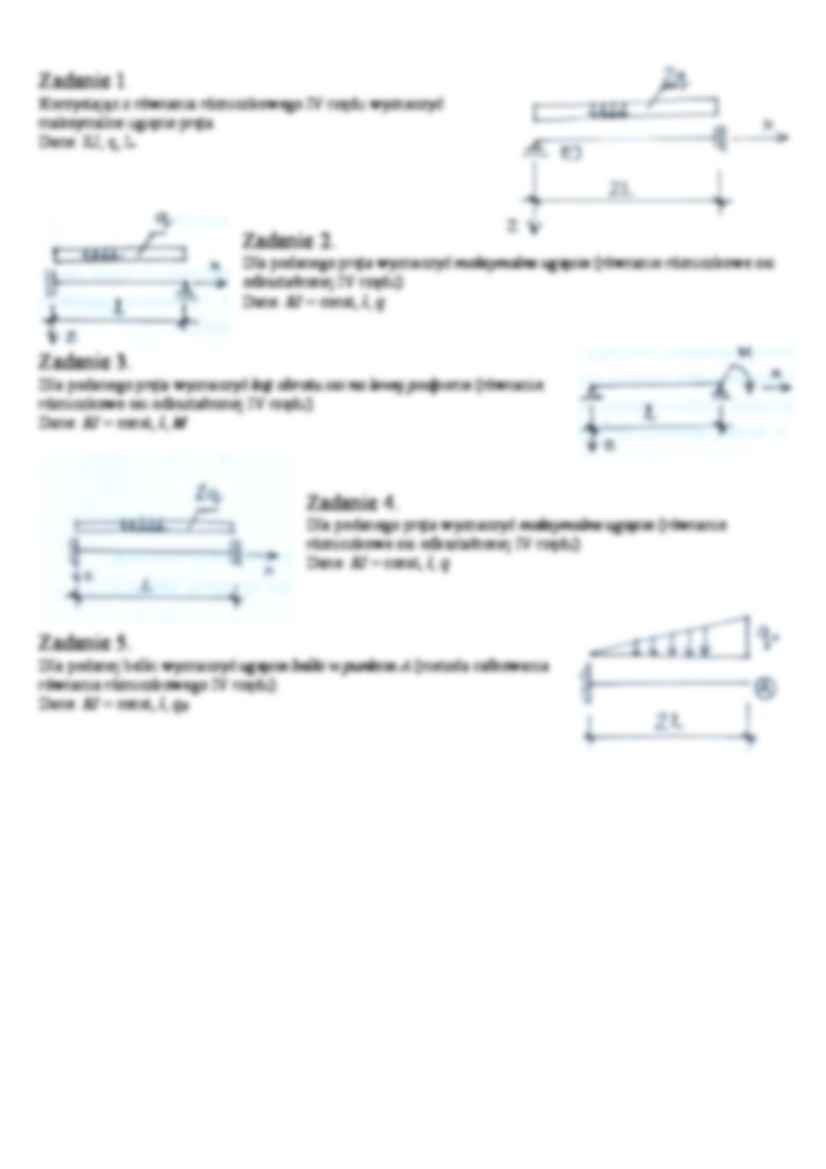
Zadanie 1.
Korzystając z równania różniczkowego IV rzędu wyznaczyć
maksymalne ugięcie pręta.
Dane: EJ, q, L
Zadanie 2.
Dla podanego pręta wyznaczyć maksymalne ugięcie (równanie różniczkowe osi
odkształconej IV rzędu).
Dane: EI = const, l, q
Zadanie 3.
Dla podanego pręta wyznaczyć kąt obrotu osi na lewej podporze (równanie
różniczkowe osi odkształconej IV rzędu).
Dane: EI = const, l, M
Zadanie 4.
Dla podanego pręta wyznaczyć maksymalne ugięcie (równanie
różniczkowe osi odkształconej IV rzędu).
Dane: EI = const, l, q
Zadanie 5.
Dla podanej belki wyznaczyć ugięcie belki w punkcie A (metoda całkowania
równania różniczkowego IV rzędu).
Dane: EI = const, l, q0
... zobacz całą notatkę




Komentarze użytkowników (0)