To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
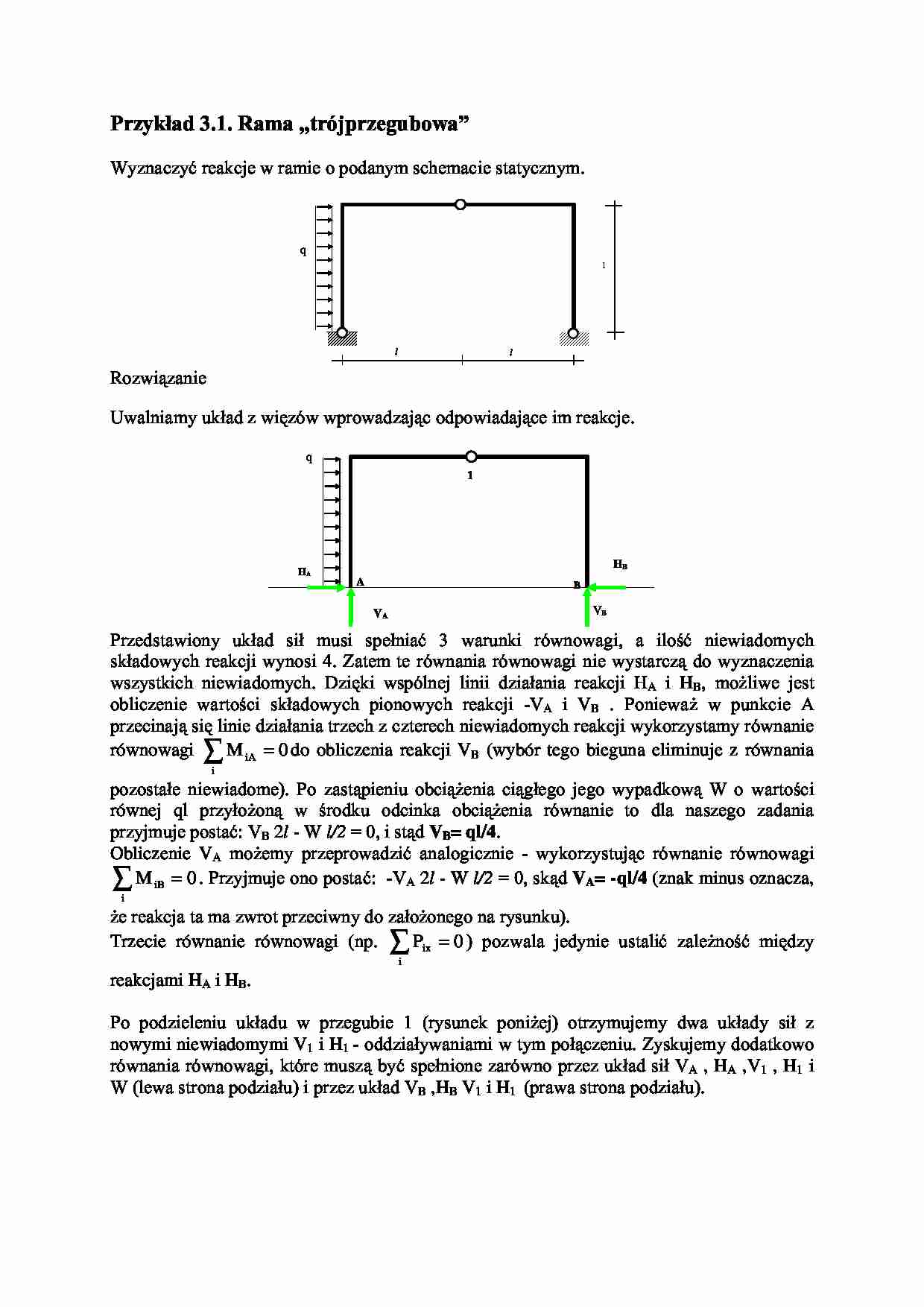


3U]\NáDG5DPDÄWUyMSU]HJXERZD´ :\]QDF]\üUHDNFMHZUDPLHRSRGDQ\PVFKHPDFLHVWDW\F]Q\P q l l l 5R]ZL]DQLH 8ZDOQLDP\XNáDG]ZL
]yZZSURZDG]DMFRGSRZLDGDMFHLPUHDNFMH q HA HB VA VB 1 A B 3U]HGVWDZLRQ\ XNáDG VLá PXVL VSHáQLDü ZDUXQNL UyZQRZDJL D LORü QLHZLDGRP\FK VNáDGRZ\FK UHDNFML Z\QRVL =DWHP WH UyZQDQLD UyZQRZDJL QLH Z\VWDUF] GR Z\]QDF]HQLD ZV]\VWNLFK QLHZLDGRP\FK ']L
NL ZVSyOQHM OLQLL G]LDáDQLD UHDNFML +A i HB PR*OLZH MHVW REOLF]HQLH ZDUWRFL VNáDGRZ\FK SLRQRZ\FK UHDNFML 9A i VB 3RQLHZD* Z SXQNFLH $ SU]HFLQDMVL
OLQLHG]LDáDQLDWU]HFK]F]WHUHFKQLHZLDGRP\FKUHDNFMLZ\NRU]\VWDP\UyZQDQLH równowagi M iA i ∑ = 0 do obliczenia reakcji V B (wybór tego bieguna eliminuje z równania SR]RVWDáH QLHZLDGRPH 3R ]DVWSLHQLX REFL*HQLD FLJáHJR MHJR Z\SDGNRZ : R ZDUWRFL równej TO SU]\áR*RQ Z URGNX RGFLQND REFL*HQLD UyZQDQLH WR GOD QDV]HJR ]DGDQLD SU]\MPXMHSRVWDü9B 2 l - W l/2 LVWG VB= ql/4 . Obliczenie VA PR*HP\ SU]HSURZDG]Lü DQDORJLF]QLH Z\NRU]\VWXMF UyZQDQLH UyZQRZDJL M iB i ∑ = 0 3U]\MPXMHRQRSRVWDü9 A 2 l - W l/2 VNG VA= -ql/4 (znak minus oznacza, *HUHDNFMDWDPD]ZURWSU]HFLZQ\GR]DáR*RQHJRQDU\VXQNX Trzecie równanie równowagi (np. P ix i ∑ = 0 SR]ZDOD MHG\QLH XVWDOLü ]DOH*QRü PL
G]\ reakcjami HA i HB. 3R SRG]LHOHQLX XNáDGX Z SU]HJXELH U\VXQHN SRQL*HM RWU]\PXMHP\ GZD XNáDG\ VLá ] nowymi niewiadomymi V1 i H1 RGG]LDá\ZDQLDPLZW\PSRáF]HQLX=\VNXMHP\GRGDWNRZR UyZQDQLDUyZQRZDJL NWyUH PXV] E\ü VSHáQLRQH ]DUyZQR SU]H] XNáDG VLá 9A , HA ,V1 , H1 i :OHZDVWURQDSRG]LDáXLSU]H]XNáDG9B ,HB V1 i H1 SUDZDVWURQDSRG]LDáX 2 W HA HB ql/4 ql/4 1 A B V1 V1 H1 H1 0DMFQDFHOXZ\]QDF]HQLHUHDNFML+A i HBZ\NRU]\VWDP\W\ONRWH]UyZQDUyZQRZDJLZ NWyU\FKQLHZ\VWSLQRZHQLHZLDGRPH91 i H13XQNWHPJG]LHSU]HFLQDMVL
OLQLHG]LDáDQLD W\FK UHDNFML MHVW SU]HJXE SU]\MPLMP\ ZL
F MDNR ELHJXQ REOLF]DQLD PRPHQWyZ WHQ SXQNW =DWHPUyZQDQLHUyZQRZDJLGODF]
FLSUDZHMSU]\MPLHSRVWDü M i prawa i 1 0 ∑ = ⇒ V B l - HB l VNG HB=ql/4 , DGODF]
FLOHZHM M i lewa i 1 0 ∑ = ⇒ ql/4 l + H A l + Wl/2 VNG HA= - 3/4q . 5R]ZL]DQLHSU]HGVWDZLDVL
QDVW
SXMFR q 3/4ql ql/4 ql/4 ql/4 C 'RVSUDZG]HQLDSRSUDZQRFLREOLF]HPR*HE\ü X*\WH QLHZ\NRU]\VWDQH ZF]HQLHMUyZQDQLH UyZQRZDJLGODFDáHJRXNáDGX3R]RVWDá\UyZQDQLD P i i η ∑ = 0RηQLHPR*HE\üSURVWRSDGáD do linii AB) lub M iC i ∑ = 0 SXQNW&QLHPR*HOH*HüQDOLQLL$% 6SUDZG]LP\F]\REOLF]RQHZDUWRFLUHDNFMLVSHáQLDMUyZQDQLHUyZQRZDJLQS M iC i ∑ = 0 . M iC i ∑ = VA 2 l - HA l- HB l+Wl/2 = ql/4 2 l – 3/4ql l - ql/4 l +ql l/2= 0. 5R]ZL]DQLHWHJR]DGDQLDPR*HSU]HELHJDüQDZLHOHVSRVREyZ,VWRWQHMHVWVSRVWU]H*HQLH*H
... zobacz całą notatkę






Komentarze użytkowników (0)