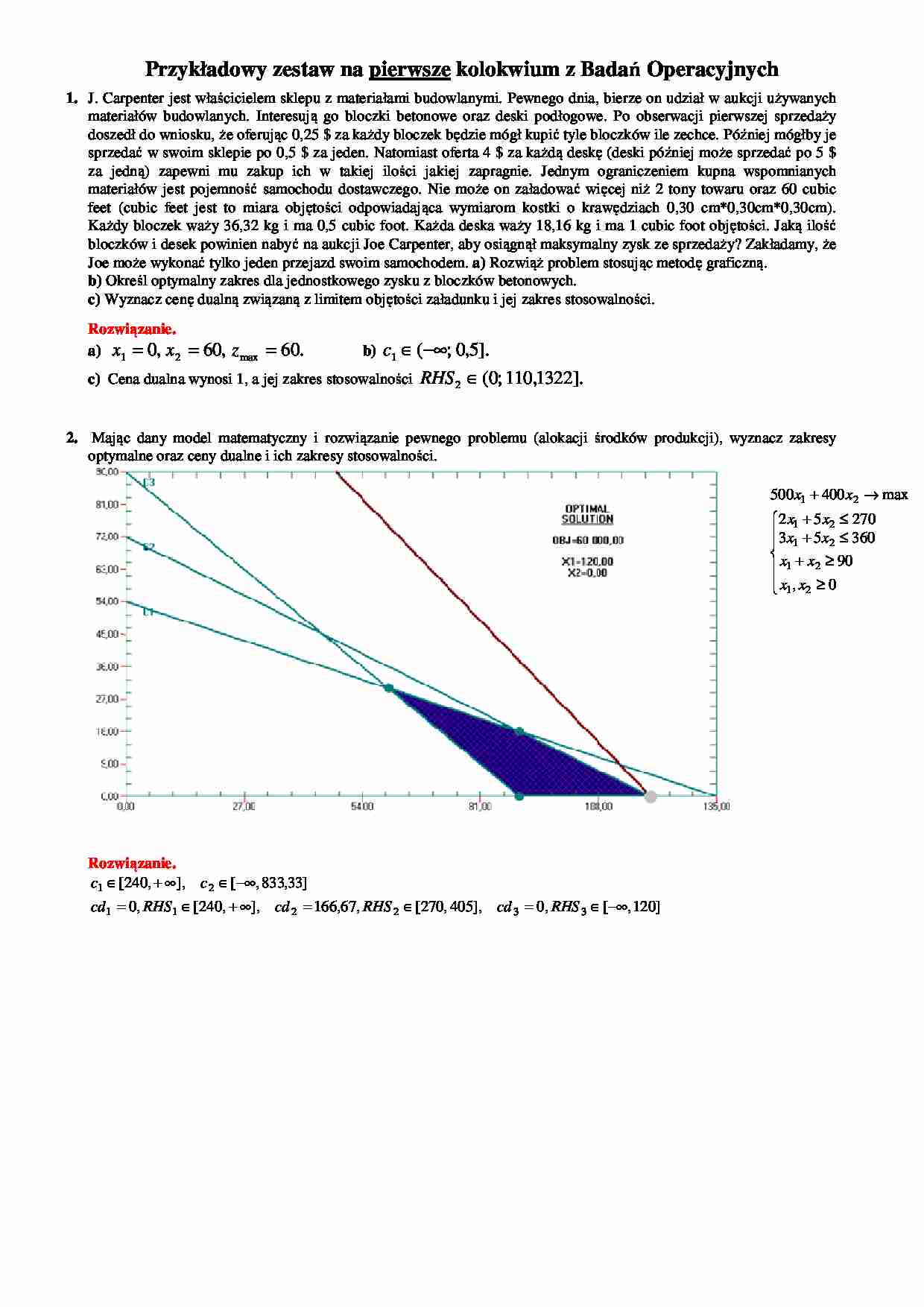
Przykładowy zestaw na pierwsze kolokwium z Badań Operacyjnych 1. J. Carpenter jest właścicielem sklepu z materiałami budowlanymi. Pewnego dnia, bierze on udział w aukcji używanych materiałów budowlanych. Interesują go bloczki betonowe oraz deski podłogowe. Po obserwacji pierwszej sprzedaży doszedł do wniosku, że oferując 0,25 $ za każdy bloczek będzie mógł kupić tyle bloczków ile zechce. Później mógłby je sprzedać w swoim sklepie po 0,5 $ za jeden. Natomiast oferta 4 $ za każdą deskę (deski później może sprzedać po 5 $ za jedną) zapewni mu zakup ich w takiej ilości jakiej zapragnie. Jednym ograniczeniem kupna wspomnianych materiałów jest pojemność samochodu dostawczego. Nie może on załadować więcej niż 2 tony towaru oraz 60 cubic feet (cubic feet jest to miara objętości odpowiadająca wymiarom kostki o krawędziach 0,30 cm*0,30cm*0,30cm). Każdy bloczek waży 36,32 kg i ma 0,5 cubic foot. Każda deska waży 18,16 kg i ma 1 cubic foot objętości. Jaką ilość bloczków i desek powinien nabyć na aukcji Joe Carpenter, aby osiągnął maksymalny zysk ze sprzedaży? Zakładamy, że Joe może wykonać tylko jeden przejazd swoim samochodem. a) Rozwiąż problem stosując metodę graficzną. b) Określ optymalny zakres dla jednostkowego zysku z bloczków betonowych. c) Wyznacz cenę dualną związaną z limitem objętości załadunku i jej zakres stosowalności. Rozwiązanie. a) . 60 , 60 , 0 max 2 1 = = = z x x b) ]. 5 , 0 ; ( 1 −∞ ∈ c c) Cena dualna wynosi 1, a jej zakres stosowalności ]. 1322 , 110 ; 0 ( 2 ∈ RHS 2. Mając dany model matematyczny i rozwiązanie pewnego problemu (alokacji środków produkcji), wyznacz zakresy optymalne oraz ceny dualne i ich zakresy stosowalności. ≥ ≥ + ≤ + ≤ + → + 0 , 90 360 5 3 270 5 2 max 400 500 2 1 2 1 2 1 2 1 2 1 x x x x x x x x x x Rozwiązanie. ] 120 , [ , 0 ], 405 , 270 [ , 67 , 166 ], , 240 [ , 0 ] 33 , 833 , [ ], , 240 [ 3 3 2 2 1 1 2 1 −∞ ∈ = ∈ = ∞ + ∈ = −∞ ∈ ∞ + ∈ RHS cd RHS cd RHS cd c c Przykładowy zestaw na pierwsze kolokwium z Badań Operacyjnych 3. P
(…)
… zastanawia się nad wprowadzeniem
do produkcji czterech nowych wzorów (W1, W2, W3, W4). Znicze-lampiony różnią się pojemnością i materiałem, z
jakiego są wykonywane. W4 – jest zniczem ceramicznym. Pozostałe są szklane, a W1 i W4 dodatkowo zdobione są
ornamentami roślinnymi, malowanymi specjalnym lakierem odpornym na ścieranie. Zysk, w groszach, na
poszczególnych zniczach wynosi odpowiednio: 15, 6, 9 i 5. Jaki jest optymalny plan produkcji, dający maksymalny
zysk i nieprzekraczający limitów trzech surowców (S1 − masa parafinowa [kg], S2 − plastikowe elementy
dekoracyjne [szt.] i S3 − lakier [l])? Na podstawie danych dotyczących technologii 15 x + 6 x + 9 x + 5 x → max
1
2
3
4
produkcji zbudowano model matematyczny (patrz obok) i następnie dokonano
0,2 x1 + 0,1x 2 + 0,5x3 + 0,1x 4 ≤ 20
rozwiązania go za pomocą…
… programu WinQSB. Niepełny wydruk z rozwiązania 3 x + 2 x + 3x ≤ 24
1
2
3
zamieszczono poniżej. Uzupełnij tabelkę o brakujące informacje, a następnie 0,07 x
+ 0,1x 4 ≤ 3
1
odpowiedz na poniższe pytania.
1
2
3
4
1
1
2
Decision
Variable
X1
X2
X3
X4
Objective
Solution Unit Cost or
Value
Profit c(j)
8
0
0
184
Function
(Max.)
Left Hand
Side
Direction
Constraint
C1
C2
C3
Total
Contribution
Reduced…
... zobacz całą notatkę



Komentarze użytkowników (0)