Ćwiczenie numer 5
Temat: Prawo podziału Nernsta
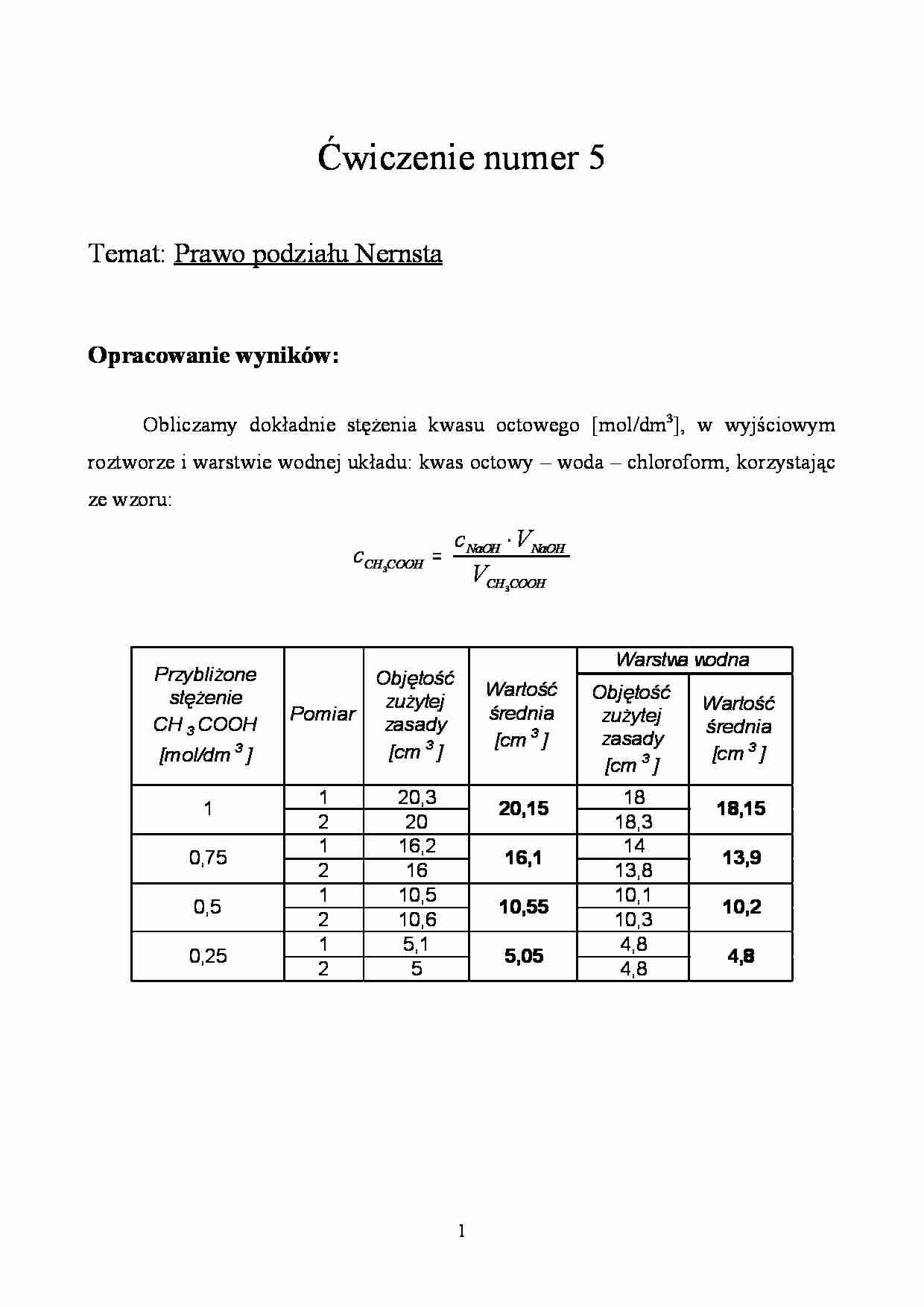
Opracowanie wyników:
Obliczamy dokładnie stężenia kwasu octowego [mol/dm3], w wyjściowym
roztworze i warstwie wodnej układu: kwas octowy – woda – chloroform, korzystając
ze wzoru:
cCH COOH =
3
c NaOH ⋅ VNaOH
VCH COOH
3
Przybliżone
stężenie
CH 3 COOH
Pomiar
1
2
1
2
1
2
1
2
20,3
20
16,2
16
10,5
10,6
5,1
5
[mol/dm 3 ]
1
0,75
0,5
0,25
Warstwa wodna
Objętość
zużytej
zasady
[cm 3 ]
Wartość
średnia
[cm 3 ]
20,15
16,1
10,55
5,05
1
Objętość
zużytej
zasady
[cm 3 ]
18
18,3
14
13,8
10,1
10,3
4,8
4,8
Wartość
średnia
[cm 3 ]
18,15
13,9
10,2
4,8
•stężenie CH3COOH w H2O:
c1 =
c2 =
c3 =
c4 =
0,1 mol dm 3 ⋅ 20,15cm 3
= 1,0075 mol 3
3
dm
2cm
0,1 mol dm 3 ⋅ 16,10cm 3
= 0,805 mol 3
dm
2cm 3
3
3
0,1 mol dm ⋅ 10,55cm
= 0,5275 mol 3
3
dm
2cm
0,1 mol dm 3 ⋅ 5,05cm 3
= 0,2525 mol 3
3
dm
2cm
•stężenie CH3COOH w CHCl3
0,1mol dm 3 ⋅ 18,15cm 3
= 0,9075 mol 3
3
dm
2cm
0,1mol dm 3 ⋅ 13,90cm 3
c2 =
= 0,695 mol 3
3
dm
2cm
0,1mol dm 3 ⋅ 10,20cm 3
c3 =
= 0,51mol 3
dm
2cm 3
c1 =
0,1mol dm 3 ⋅ 4,80cm 3
c4 =
= 0,24 mol 3
3
dm
2cm
Obliczanie współczynnika podziału K:
c1
n
c2
K=
gdzie: c1 – stężenie substancji rozpuszczonej (CH3COOH) w wodzie,
c2 – stężenie substancji rozpuszczonej (CH3COOH) w chloroformie,
n – liczba wskazująca ile razy masa cząsteczkowa M1 substancji
rozpuszczonej w pierwszym rozpuszczalniku jest większa od masy
cząsteczkowej M2 tej samej substancji, rozpuszczonej w drugim
rozpuszczalniku: n = M1/M2.
W tym przypadku przyjmujemy n = 1.
2
1,0075
≈ 1,11
0,9075
0,805
K=
≈ 1,16
0,695
0,5275
K=
≈ 1,03
0,51
0,2525
K=
≈ 1,05
0,24
K=
c1
c2
log c1
1,0075 0,9075 0,003245055
0,805
0,695
-0,09420412
0,5275
0,51
-0,277777536
0,2525
0,24
-0,597738618
log c2
-0,042153366
-0,158015195
-0,292429824
-0,619788758
K
1,11
1,16
1,03
1,05
Kgraf
Wyznaczanie współczynników prostej:
Metodą najmniejszych kwadratów obliczanie parametrów prostej log c1 = f (log c2)
n
a=
n∑ xi yi −
i= 1
n
∑ x∑
i
i= 1
i= 1
n x
n∑ x − ∑ i
i= 1
i= 1
n
n
b=
n
∑
x
i= 1
2
i
yi
2
2
i
n
∑
i= 1
yi −
n
n
∑ x∑
i= 1
i
i= 1
n x
n∑ x − ∑ i
i= 1
i= 1
n
xi yi
2
2
i
n – liczba pomiarów
Σ
log c1 [y]
0,003245055
-0,09420412
-0,277777536
-0,597738618
-0,966475218
log c2 [x]
-0,042153366
-0,158015195
-0,292429824
-0,619788758
-1,112387144
3
2
x
0,001776906
0,024968802
0,085515202
0,384138105
0,496399015
x*y
-0,00013679
0,014885682
0,081230436
0,370471676
0,466451004
a=
4 ⋅ 0,466451004 − ( − 1,112387144) ⋅ ( − 0,966475218)
= 1,0568
2
4 ⋅ 0,496399015 − ( − 1,112387144)
b=
0, 496399015 ⋅ ( − 0,966475218) − ( − 1,112387144 ) ⋅ 0,466451004
= 0,0523
2
4 ⋅ 0,496399015 − ( − 1,112387144 )
y = 1,0568 x + 0,0523
Wnioski:
Współczynnik K w zależności od roztworu różni się nieznacznie od siebie.
Spowodowane jest to na przykład błędem miareczkowania.
4
... zobacz całą notatkę





Komentarze użytkowników (0)