To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
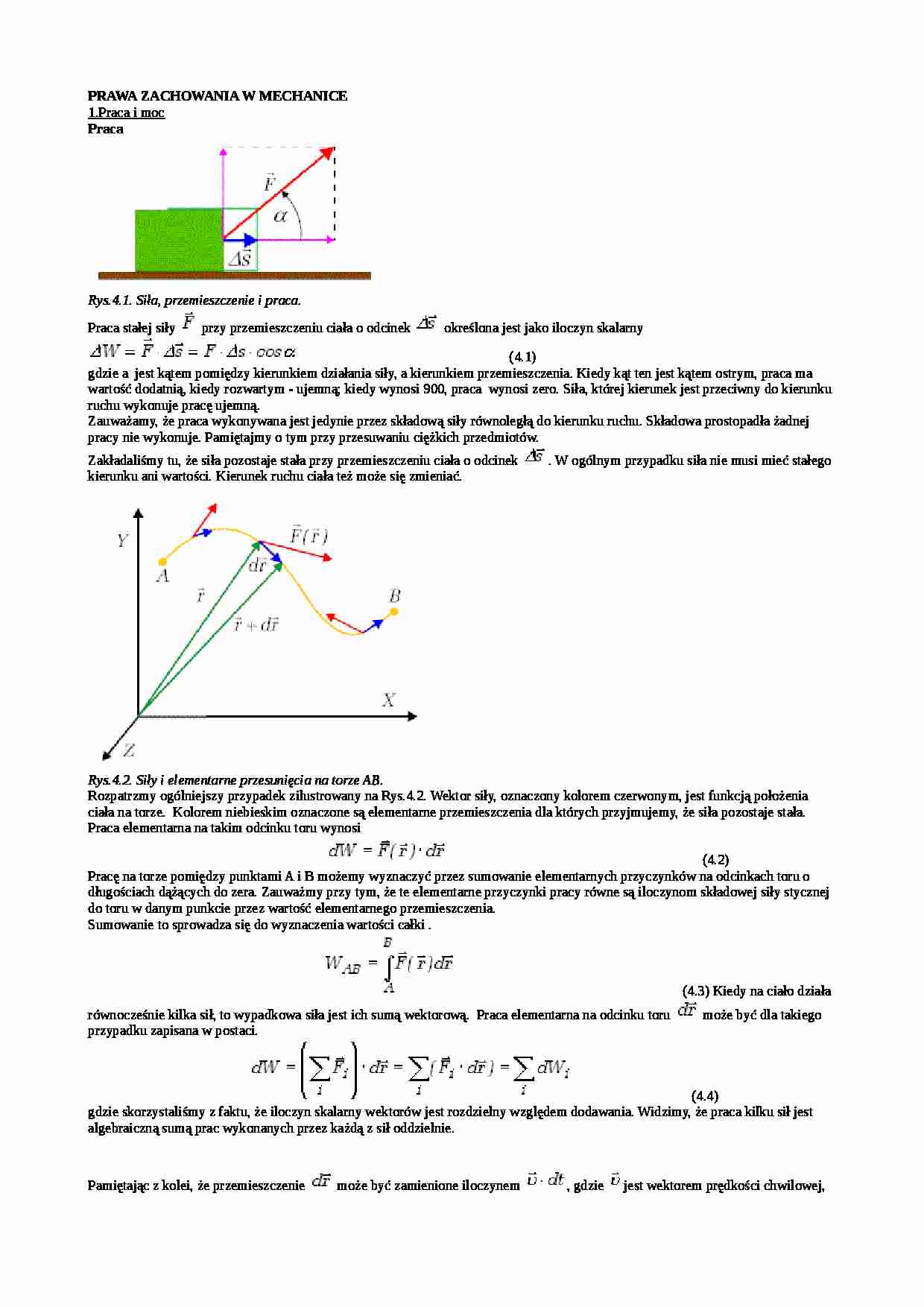


PRAWA ZACHOWANIA W MECHANICE 1.Praca i moc Praca Rys.4.1. Siła, przemieszczenie i praca. Praca stałej siły przy przemieszczeniu ciała o odcinek określona jest jako iloczyn skalarny (4.1)
gdzie a jest kątem pomiędzy kierunkiem działania siły, a kierunkiem przemieszczenia. Kiedy kąt ten jest kątem ostrym, praca ma wartość dodatnią, kiedy rozwartym - ujemną; kiedy wynosi 900, praca wynosi zero. Siła, której kierunek jest przeciwny do kierunku ruchu wykonuje pracę ujemną. Zauważamy, że praca wykonywana jest jedynie przez składową siły równoległą do kierunku ruchu. Składowa prostopadła żadnej pracy nie wykonuje. Pamiętajmy o tym przy przesuwaniu ciężkich przedmiotów. Zakładaliśmy tu, że siła pozostaje stała przy przemieszczeniu ciała o odcinek . W ogólnym przypadku siła nie musi mieć stałego kierunku ani wartości. Kierunek ruchu ciała też może się zmieniać. Rys.4.2. Siły i elementarne przesunięcia na torze AB. Rozpatrzmy ogólniejszy przypadek zilustrowany na Rys.4.2. Wektor siły, oznaczony kolorem czerwonym, jest funkcją położenia ciała na torze. Kolorem niebieskim oznaczone są elementarne przemieszczenia dla których przyjmujemy, że siła pozostaje stała. Praca elementarna na takim odcinku toru wynosi (4.2)
Pracę na torze pomiędzy punktami A i B możemy wyznaczyć przez sumowanie elementarnych przyczynków na odcinkach toru o długościach dążących do zera. Zauważmy przy tym, że te elementarne przyczynki pracy równe są iloczynom składowej siły stycznej do toru w danym punkcie przez wartość elementarnego przemieszczenia. Sumowanie to sprowadza się do wyznaczenia wartości całki . (4.3) Kiedy na ciało działa równocześnie kilka sił, to wypadkowa siła jest ich sumą wektorową. Praca elementarna na odcinku toru może być dla takiego przypadku zapisana w postaci.
(4.4) gdzie skorzystaliśmy z faktu, że iloczyn skalarny wektorów jest rozdzielny względem dodawania. Widzimy, że praca kilku sił jest algebraiczną sumą prac wykonanych przez każdą z sił oddzielnie.
Pamiętając z kolei, że przemieszczenie może być zamienione iloczynem , gdzie jest wektorem prędkości chwilowej, możemy pracę wykonaną w przedziale czasu od do wyrazić jako.
(…)
… wyłącznie siły zachowawcze. Wówczas ubytkowi energii potencjalnej towarzyszy zawsze równy mu co do wartości bezwzględnej przyrost energii kinetycznej i vice versa.
Kiedy na ciało działają siły dyssypatywne zasada zachowania energii mechanicznej nie jest spełniona. Siły te zmieniają energię mechaniczną ciała. Następuje zamiana energii mechanicznej na inne rodzaje energii, np. energię cieplną, chemiczną…
… lotu, Fot 4.3. Warto też dodać, że pęd układu nie może być zamieniony na coś innego, w odróżnieniu od energii mechanicznej, która może ulec zamianie na inne rodzaje energii. Zasada zachowania pędu obowiązuje więc także w procesach, w których naruszona jest zasada zachowania energii mechanicznej.
Fot.4.3. Kształty rozpryskujących się fajerwerków odzwierciedlają bardzo efektownie zasadę zachowania pędu…
…, do którego siła ta jest przyłożona.
Za jednostkę pracy przyjmuje się pracę jednostkowej siły przy przesunięciu równym jednostce długości i kącie pomiędzy wektorami siły i przesunięcia równym zeru. Jednostką pracy w układzie SI jest jeden dżul ( )
Jednostką mocy jest taka moc, kiedy jednostkowa praca wykonana jest w jednostce czasu.
Jednostką mocy w układzie SI jest jeden wat ( ).
2. Siły zachowawcze…
… lub rozpraszającą. Przykładem siły zachowawczej jest siła ciążenia, oraz znana nam już siła sprężystości. Do sił dyssypatywnych zaliczamy siły tarcia i siły oporu powietrza. W dalszej części kursu poznamy jeszcze inne przykłady obu rodzajów sił.
3. Energia potencjalna i kinetyczna Energia, to możliwość wykonania pracy, zaś praca wykonana nad ciałem zmienia jego energię. Energia mechaniczna może występować…
…, gdy pracę nad ciałem przy przesunięciu z punktu A do B wykonują wyłącznie siły zachowawcze. (4.14) Z wzoru tego wynika natychmiast, że (4.14a) Widzimy, że suma energii potencjalnej i kinetycznej dla punktów A i B na drodze poruszającego się ciała jest taka sama. Punkty te są dowolnie wybranymi punktami na torze. Oznacza to, że suma obu rodzajów energii, stanowiąca całkowitą energię mechaniczną ciała…
... zobacz całą notatkę






Komentarze użytkowników (0)