To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
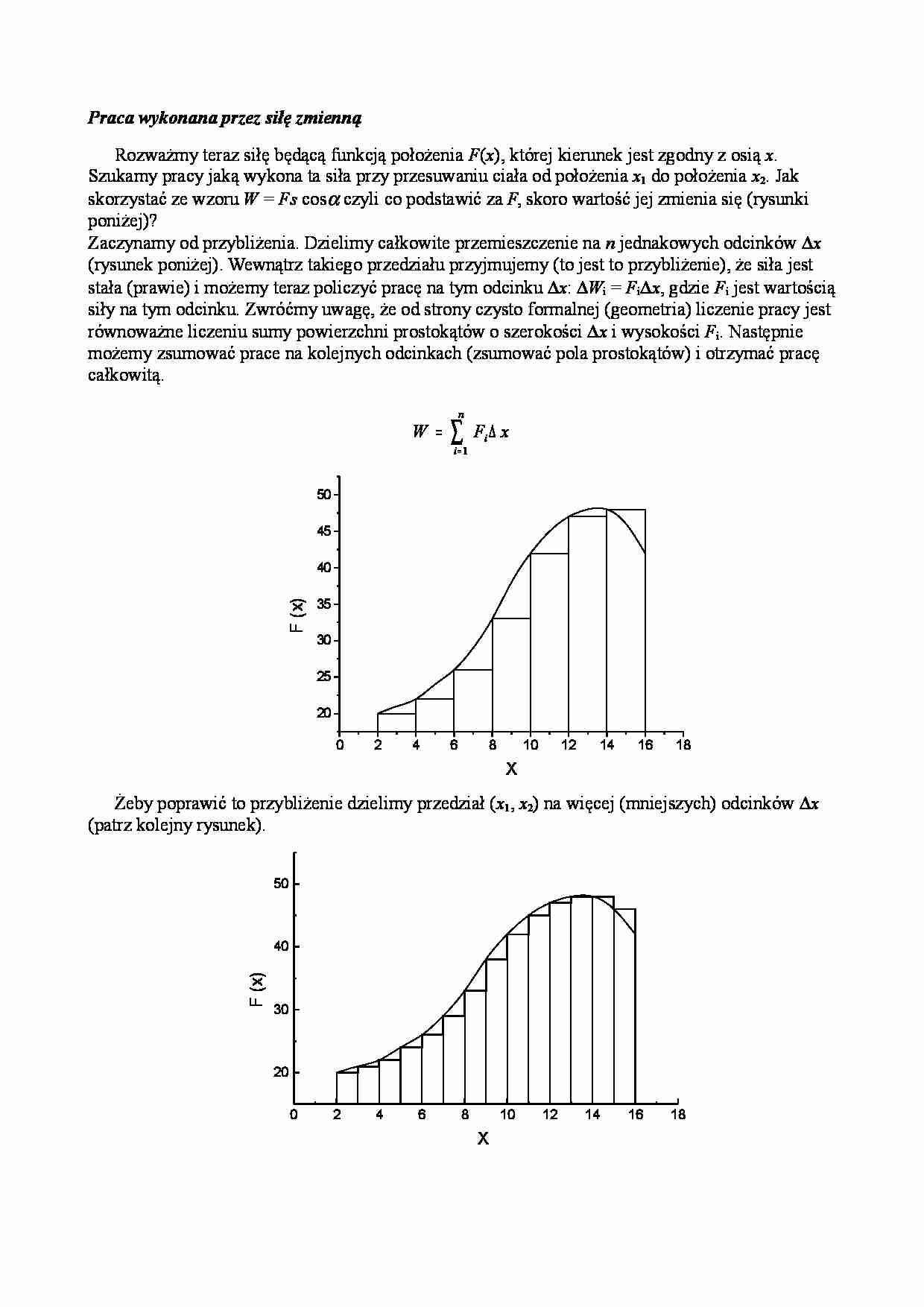


Praca wykonana przez siłę zmienną Rozważmy teraz siłę będącą funkcją położenia F ( x ), której kierunek jest zgodny z osią x . Szukamy pracy jaką wykona ta siła przy przesuwaniu ciała od położenia x 1 do położenia x 2. Jak skorzystać ze wzoru W = Fs cos α czyli co podstawić za F , skoro wartość jej zmienia się (rysunki poniżej)? Zaczynamy od przybliżenia. Dzielimy całkowite przemieszczenie na n jednakowych odcinków ∆ x (rysunek poniżej). Wewnątrz takiego przedziału przyjmujemy (to jest to przybliżenie), że siła jest stała (prawie) i możemy teraz policzyć pracę na tym odcinku ∆ x : ∆ W i = F i∆ x , gdzie F i jest wartością siły na tym odcinku. Zwróćmy uwagę, że od strony czysto formalnej (geometria) liczenie pracy jest równoważne liczeniu sumy powierzchni prostokątów o szerokości ∆ x i wysokości F i. Następnie możemy zsumować prace na kolejnych odcinkach (zsumować pola prostokątów) i otrzymać pracę całkowitą. ∑ = ∆ = n i i x F W 1 Żeby poprawić to przybliżenie dzielimy przedział ( x 1, x 2) na więcej (mniejszych) odcinków ∆ x (patrz kolejny rysunek). 0 2 4 6 8 10 12 14 16 18 20 25 30 35 40 45 50 F ( x) X 0 2 4 6 8 10 12 14 16 18 20 30 40 50 F ( x) X I teraz znowu powtarzamy procedurę sumowania. Przybliżenie jest lepsze bo siła ma prawie stałą wartość wewnątrz "małych" przedziałów ∆ x (pola powierzchni prostokątów bardziej pokrywają się z polem pod krzywą). Widać, że rozwiązaniem problemu jest przejście (w granicy) ∆ x → 0. Stosujemy tę samą procedurę obliczając ∑ ∫ = ∆ = → ∆ 2 1 2 1 d lim 0 x x x x x x F x F W (7.2) To jest definicja całki. Liczbowo odpowiada to liczeniu pola powierzchni pod krzywą (w zadanym przedziale - granicach). Odpowiada to też z definicji liczeniu wartości średniej co zgadza się z intuicyjnym podejściem: W = Fśrednia ( x 2 – x 1) Trzeba więc albo umieć rozwiązać całkę (albo poszukać w tablicach) lub umieć obliczyć pole powierzchni pod krzywą co może być czasem łatwe. Np. rozważmy sprężynę zamocowaną jednym końcem do ściany i rozciąganą siłą F tak, że jej koniec przemieszcza się o x . Siła wywierana przez sprężynę jest siłą przywracającą równowagę i wynosi F = - k x . Aby rozciągnąć sprężynę musimy przyłożyć siłę równą co do wartości lecz przeciwnie skierowaną. Tak więc F = k x . Teraz obliczmy pracę ∫ ∫ = = =
... zobacz całą notatkę






Komentarze użytkowników (0)